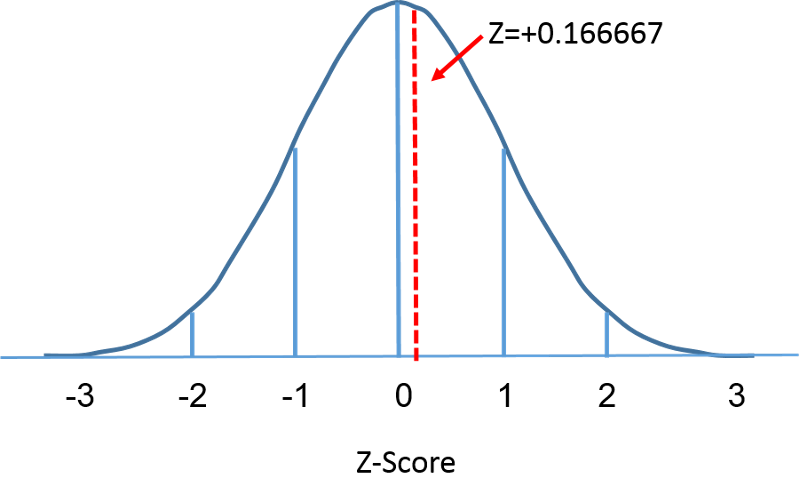
Die Standardnormalverteilung ist eine Normalverteilung mit einem Mittelwert von Null und einer Standardabweichung von 1. Die Standardnormalverteilung ist bei Null zentriert, und das Ausmaß, in dem eine bestimmte Messung vom Mittelwert abweicht, wird durch die Standardabweichung angegeben. Bei der Standardnormalverteilung liegen 68 % der Beobachtungen innerhalb von 1 Standardabweichung vom Mittelwert, 95 % liegen innerhalb von 2 Standardabweichungen vom Mittelwert und 99,9 % liegen innerhalb von 3 Standardabweichungen vom Mittelwert. Bis zu diesem Punkt haben wir „X“ verwendet, um die Variable von Interesse zu bezeichnen (z. B. X=BMI, X=Größe, X=Gewicht). Bei Verwendung einer Standardnormalverteilung wird jedoch „Z“ verwendet, um eine Variable im Kontext einer Standardnormalverteilung zu bezeichnen. Nach der Normierung liegt der auf der vorigen Seite besprochene BMI=30 0,16667 Einheiten über dem Mittelwert von 0 in der Standardnormalverteilung auf der rechten Seite.
 ====
====
Da die Fläche unter der Standardkurve = 1 ist, können wir beginnen, die Wahrscheinlichkeiten bestimmter Beobachtungen genauer zu definieren. Für jeden gegebenen Z-Score können wir die Fläche unter der Kurve links von diesem Z-Score errechnen. Die Tabelle im Rahmen unten zeigt die Wahrscheinlichkeiten für die Standardnormalverteilung. Betrachten Sie die Tabelle und stellen Sie fest, dass ein Z-Wert von 0,0 eine Wahrscheinlichkeit von 0,50 oder 50 % und ein Z-Wert von 1, d. h. eine Standardabweichung über dem Mittelwert, eine Wahrscheinlichkeit von 0,8413 oder 84 % angibt. Das liegt daran, dass eine Standardabweichung über und unter dem Mittelwert etwa 68 % der Fläche umfasst, so dass eine Standardabweichung über dem Mittelwert die Hälfte davon, nämlich 34 %, ausmacht. Die 50% unter dem Mittelwert plus die 34% über dem Mittelwert ergeben also 84%.
Wahrscheinlichkeiten der Standardnormalverteilung Z
![]()
Diese Tabelle ist so aufgebaut, dass sie die Fläche unter der Kurve links von oder kleiner als ein bestimmter Wert oder „Z-Wert“ angibt. Da in diesem Fall der Mittelwert gleich Null und die Standardabweichung gleich 1 ist, ist der Z-Wert die Anzahl der Standardabweichungseinheiten, die vom Mittelwert entfernt sind, und die Fläche ist die Wahrscheinlichkeit, einen Wert zu beobachten, der kleiner als dieser bestimmte Z-Wert ist. Beachten Sie auch, dass die Tabelle Wahrscheinlichkeiten mit zwei Nachkommastellen von Z anzeigt. Die Einerstelle und die erste Nachkommastelle werden in der linken Spalte angezeigt, und die zweite Nachkommastelle wird in der oberen Zeile angezeigt.
Aber kommen wir zurück zur Frage nach der Wahrscheinlichkeit, dass der BMI unter 30 liegt, d.h. P(X<30). Wir können diese Frage mit Hilfe der Standardnormalverteilung beantworten. Die folgenden Abbildungen zeigen die Verteilungen des BMI für Männer im Alter von 60 Jahren und die Standardnormalverteilung nebeneinander.
Verteilung des BMI und Standardnormalverteilung
 ====
====
Die Fläche unter jeder Kurve ist gleich, aber die Skalierung der X-Achse ist unterschiedlich. Es ist jedoch zu beachten, dass die Flächen links der gestrichelten Linie die gleichen sind. Die BMI-Verteilung reicht von 11 bis 47, während die standardisierte Normalverteilung, Z, von -3 bis 3 reicht. Wir wollen P(X < 30) berechnen. Dazu können wir den Z-Wert bestimmen, der X = 30 entspricht, und dann die obige Tabelle der Standardnormalverteilung verwenden, um die Wahrscheinlichkeit oder die Fläche unter der Kurve zu ermitteln. Die folgende Formel wandelt einen X-Wert in einen Z-Wert um, der auch als standardisierter Wert bezeichnet wird:

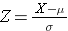
wobei μ der Mittelwert und σ die Standardabweichung der Variablen X ist.
Um P(X < 30) zu berechnen, wandeln wir X=30 in den entsprechenden Z-Score um (dies wird als Standardisierung bezeichnet):

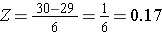
Weiteres Beispiel
Wie groß ist die Wahrscheinlichkeit, dass ein Mann im Alter von 60 Jahren einen BMI von mehr als 35 hat, wenn man die gleiche Verteilung für den BMI verwendet? Mit anderen Worten: Wie groß ist P(X > 35)? Wieder standardisieren wir:

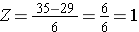
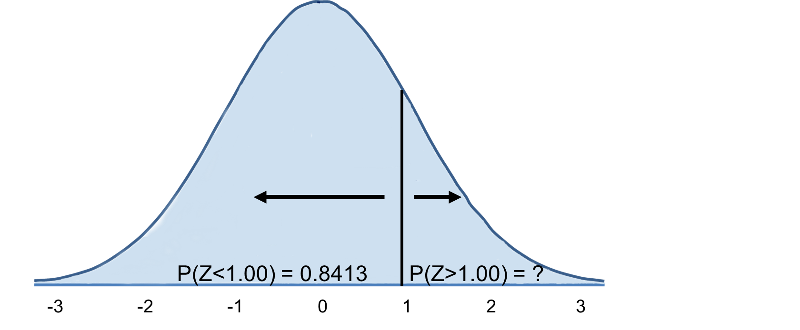
Daher ist P(Z>1)=1-0.8413=0.1587. Interpretation: Fast 16% der Männer im Alter von 60 Jahren haben einen BMI über 35.
Normalwahrscheinlichkeitsrechner
![]()
![]()
Z-Scores mit R
Alternativ zum Nachschlagen von Normalwahrscheinlichkeiten in der Tabelle oder zur Verwendung von Excel können wir R zur Berechnung von Wahrscheinlichkeiten verwenden. Beispiel:
> pnorm(0)
Ein Z-Score von 0 (der Mittelwert einer beliebigen Verteilung) hat 50 % der Fläche auf der linken Seite. Wie hoch ist die Wahrscheinlichkeit, dass ein 60-jähriger Mann in der obigen Population einen BMI von weniger als 29 (den Mittelwert) hat? Der Z-Score wäre 0, und pnorm(0)=0,5 oder 50%.
Wie groß ist die Wahrscheinlichkeit, dass ein 60-jähriger Mann einen BMI von weniger als 30 hat? Der Z-Score beträgt 0,16667.
> pnorm(0,16667)
Die Wahrscheinlichkeit beträgt also 56,6%.
Wie hoch ist die Wahrscheinlichkeit, dass ein 60-jähriger Mann einen BMI von mehr als 35 hat?
35-29=6, das ist eine Standardabweichung über dem Mittelwert. Wir können also die Fläche links
> von pnorm(1)
berechnen und dann das Ergebnis von 1,0 abziehen.
1-0,8413447= 0,1586553
Die Wahrscheinlichkeit, dass ein 60-jähriger Mann einen BMI von mehr als 35 hat, beträgt also 15,8%.
Oder wir können R verwenden, um das Ganze in einem einzigen Schritt wie folgt zu berechnen:
> 1-pnorm(1)
Wahrscheinlichkeit für einen Wertebereich

Wie hoch ist die Wahrscheinlichkeit, dass ein 60-jähriger Mann einen BMI zwischen 30 und 35 hat? Dies ist dasselbe wie die Frage, welcher Anteil der Männer im Alter von 60 Jahren einen BMI zwischen 30 und 35 hat. Genauer gesagt, wollen wir P(30 < X < 35)? Wir haben zuvor P(30<X) und P(X<35) berechnet; wie können diese beiden Ergebnisse verwendet werden, um die Wahrscheinlichkeit zu berechnen, dass der BMI zwischen 30 und 35 liegt? Versuchen Sie, die Antwort selbst zu formulieren, bevor Sie sich die folgende Erklärung ansehen.
Antwort