Standardní normální rozdělení je normální rozdělení se střední hodnotou nula a směrodatnou odchylkou 1. Standardní normální rozdělení má střed v nule a míra odchylky daného měření od střední hodnoty je dána směrodatnou odchylkou. Pro standardní normální rozdělení platí, že 68 % pozorování leží do 1 směrodatné odchylky od průměru, 95 % leží do 2 směrodatných odchylek od průměru a 99,9 % leží do 3 směrodatných odchylek od průměru. Až do této chvíle jsme používali „X“ pro označení proměnné, která nás zajímá (např. X=BMI, X=výška, X=hmotnost). Při použití standardního normálního rozdělení však budeme pro označení proměnné v kontextu standardního normálního rozdělení používat „Z“. Po normalizaci je níže uvedeno, že BMI=30, o kterém jsme hovořili na předchozí straně, leží 0,16667 jednotky nad střední hodnotou 0 na standardním normálním rozdělení vpravo.
 ====
====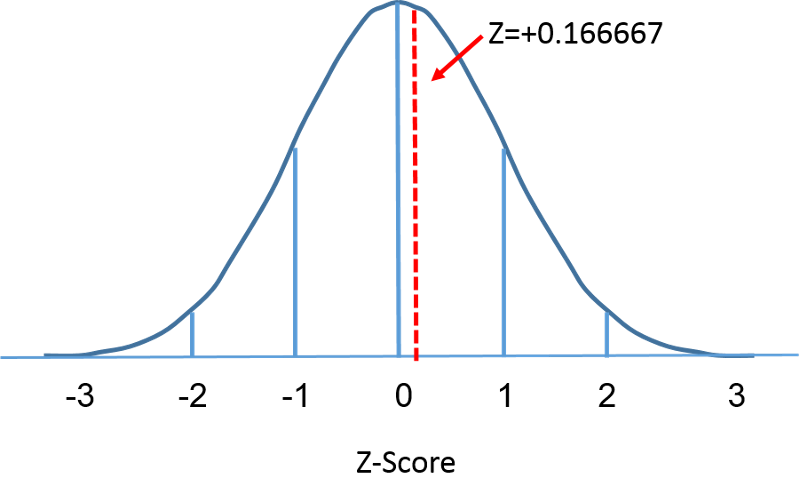
Protože plocha pod standardní křivkou = 1, můžeme začít přesněji definovat pravděpodobnosti konkrétního pozorování. Pro libovolné dané Z-skóre můžeme vypočítat plochu pod křivkou nalevo od tohoto Z-skóre. Tabulka v rámečku níže ukazuje pravděpodobnosti pro standardní normální rozdělení. Prozkoumejte tabulku a všimněte si, že skóre „Z“ 0,0 uvádí pravděpodobnost 0,50 neboli 50 % a skóre „Z“ 1, což znamená jednu směrodatnou odchylku nad průměrem, uvádí pravděpodobnost 0,8413 neboli 84 %. To proto, že jedna směrodatná odchylka nad a pod průměrem zahrnuje přibližně 68 % plochy, takže jedna směrodatná odchylka nad průměrem představuje polovinu, tedy 34 %. Takže 50 % pod průměrem plus 34 % nad průměrem nám dává 84 %.
Pravděpodobnosti standardního normálního rozdělení Z
![]()
Tato tabulka je uspořádána tak, aby poskytovala plochu pod křivkou vlevo nebo menší než zadaná hodnota neboli „hodnota Z“. V tomto případě, protože průměr je nula a směrodatná odchylka je 1, je hodnota Z počet jednotek směrodatné odchylky od průměru a plocha je pravděpodobnost pozorování hodnoty menší než tato konkrétní hodnota Z. Všimněte si také, že tabulka zobrazuje pravděpodobnosti na dvě desetinná místa Z. Místo jednotek a první desetinné místo jsou uvedeny v levém sloupci a druhé desetinné místo je zobrazeno napříč horním řádkem.
Vraťme se však k otázce týkající se pravděpodobnosti, že BMI je menší než 30, tedy P(X<30). Na tuto otázku můžeme odpovědět pomocí standardního normálního rozdělení. Na obrázcích níže jsou vedle sebe zobrazena rozdělení BMI pro muže ve věku 60 let a standardní normální rozdělení.
Rozdělení BMI a standardní normální rozdělení
 ====
====
Plocha pod každou křivkou je jedna, ale měřítko osy X je jiné. Všimněte si však, že plochy nalevo od přerušované čáry jsou stejné. Rozdělení BMI se pohybuje od 11 do 47, zatímco standardizované normální rozdělení, Z, se pohybuje od -3 do 3. Chceme vypočítat P(X < 30). Za tímto účelem můžeme určit hodnotu Z, která odpovídá X = 30, a poté pomocí výše uvedené tabulky standardního normálního rozdělení zjistit pravděpodobnost nebo plochu pod křivkou. Následující vzorec převádí hodnotu X na skóre Z, které se také nazývá standardizované skóre:

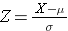
kde μ je průměr a σ je směrodatná odchylka proměnné X.
Pro výpočet P(X < 30) převedeme X=30 na odpovídající Z skóre (tomu se říká standardizace):

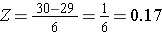
Další příklad
Při použití stejného rozdělení pro BMI, jaká je pravděpodobnost, že muž ve věku 60 let má BMI vyšší než 35? Jinými slovy, jaká je hodnota P(X > 35)? Opět standardizujeme:

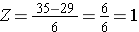
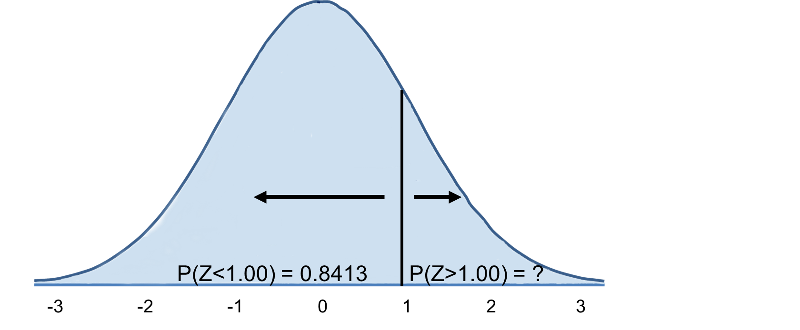
Tedy P(Z>1)=1-0,8413=0,1587. Interpretace: Téměř 16 % mužů ve věku 60 let má BMI vyšší než 35.
Kalkulátor normální pravděpodobnosti
![]()
![]()
Z-skóre s R
Aternativně k vyhledání normální pravděpodobnosti v tabulce nebo pomocí Excelu můžeme k výpočtu pravděpodobnosti použít R. Například
> pnorm(0)
Z-skóre 0 (střední hodnota libovolného rozdělení) má 50 % plochy vlevo. Jaká je pravděpodobnost, že 60letý muž z výše uvedené populace má BMI menší než 29 (průměr)? Z-skóre by bylo 0 a pnorm(0)=0,5 neboli 50 %.
Jaká je pravděpodobnost, že 60letý muž bude mít BMI menší než 30? Z-skóre bylo 0,16667.
> pnorm(0,16667)
Takže pravděpodobnost je 56,6 %.
Jaká je pravděpodobnost, že 60letý muž bude mít BMI větší než 35?
35-29=6, což je jedna směrodatná odchylka nad průměrem. Můžeme tedy vypočítat plochu vlevo
> pnorm(1)
a výsledek pak odečíst od 1,0.
1-0,8413447= 0,1586553
Takže pravděpodobnost, že 60letý muž bude mít BMI větší než 35, je 15,8 %.
Nebo můžeme použít program R a celou věc vypočítat v jednom kroku takto:
> 1-pnorm(1)
Pravděpodobnost pro rozsah hodnot

Jaká je pravděpodobnost, že muž ve věku 60 let má BMI mezi 30 a 35? Všimněte si, že to je totéž jako otázka, jaký podíl mužů ve věku 60 let má BMI mezi 30 a 35. Konkrétně chceme zjistit P(30 < X < 35)? Předtím jsme vypočítali P(30<X) a P(X<35); jak lze tyto dva výsledky použít k výpočtu pravděpodobnosti, že BMI bude mezi 30 a 35? Pokuste se formulovat a odpovědět sami, než se podíváte na vysvětlení níže.
Odpověď
.