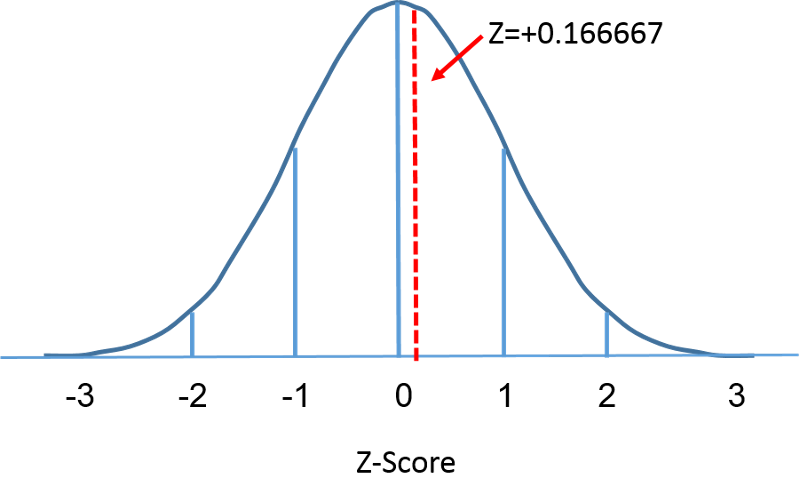
La distribution normale standard est une distribution normale avec une moyenne de zéro et un écart-type de 1. La distribution normale standard est centrée sur zéro et le degré auquel une mesure donnée s’écarte de la moyenne est donné par l’écart-type. Pour la distribution normale standard, 68 % des observations se situent à moins d’un écart-type de la moyenne ; 95 % se situent à moins de deux écarts-type de la moyenne ; et 99,9 % se situent à moins de trois écarts-type de la moyenne. Jusqu’à présent, nous avons utilisé « X » pour désigner la variable d’intérêt (par exemple, X=BMI, X=taille, X=poids). Cependant, lorsque nous utilisons une distribution normale standard, nous utiliserons « Z » pour désigner une variable dans le contexte d’une distribution normale standard. Après normalisation, l’IMC=30 discuté à la page précédente est représenté ci-dessous se situant 0,16667 unités au-dessus de la moyenne de 0 sur la distribution normale standard à droite.
 ====
====
Puisque l’aire sous la courbe standard = 1, nous pouvons commencer à définir plus précisément les probabilités d’une observation spécifique. Pour n’importe quel score Z donné, nous pouvons calculer l’aire sous la courbe à gauche de ce score. Le tableau dans le cadre ci-dessous montre les probabilités pour la distribution normale standard. Examinez le tableau et notez qu’un score « Z » de 0,0 indique une probabilité de 0,50 ou 50 %, et qu’un score « Z » de 1, c’est-à-dire un écart-type au-dessus de la moyenne, indique une probabilité de 0,8413 ou 84 %. Cela s’explique par le fait qu’un écart type au-dessus et au-dessous de la moyenne englobe environ 68 % de la surface, et qu’un écart type au-dessus de la moyenne représente donc la moitié de cette surface, soit 34 %. Donc, les 50% en dessous de la moyenne plus les 34% au-dessus de la moyenne nous donnent 84%.
Probabilités de la distribution normale standard Z
![]()
Ce tableau est organisé pour fournir l’aire sous la courbe à gauche ou en dessous d’une valeur spécifiée ou « valeur Z ». Dans ce cas, comme la moyenne est égale à zéro et que l’écart-type est égal à 1, la valeur Z est le nombre d’unités d’écart-type par rapport à la moyenne, et l’aire est la probabilité d’observer une valeur inférieure à cette valeur Z particulière. Notez également que le tableau indique les probabilités à deux décimales de Z. La place des unités et la première décimale sont indiquées dans la colonne de gauche, et la deuxième décimale est affichée en travers de la ligne supérieure.
Mais revenons à la question sur la probabilité que l’IMC soit inférieur à 30, c’est-à-dire P(X<30). Nous pouvons répondre à cette question en utilisant la distribution normale standard. Les figures ci-dessous montrent côte à côte les distributions de l’IMC pour les hommes âgés de 60 ans et la distribution normale standard.
Distribution de l’IMC et distribution normale standard
 ====
====
L’aire sous chaque courbe est la même, mais l’échelle de l’axe des X est différente. Notez cependant que les aires à gauche de la ligne pointillée sont les mêmes. La distribution de l’IMC va de 11 à 47, tandis que la distribution normale standardisée, Z, va de -3 à 3. Nous voulons calculer P(X < 30). Pour ce faire, nous pouvons déterminer la valeur Z qui correspond à X = 30, puis utiliser le tableau de la distribution normale standardisée ci-dessus pour trouver la probabilité ou l’aire sous la courbe. La formule suivante convertit une valeur X en un score Z, également appelé score standardisé :

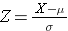
où μ est la moyenne et σ est l’écart-type de la variable X.
Pour calculer P(X < 30), nous convertissons le X=30 en son score Z correspondant (cela s’appelle normaliser) :

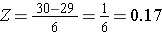
Autre exemple
En utilisant la même distribution pour l’IMC, quelle est la probabilité qu’un homme âgé de 60 ans ait un IMC supérieur à 35 ? En d’autres termes, quelle est P(X > 35) ? Encore une fois, nous normalisons :

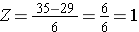
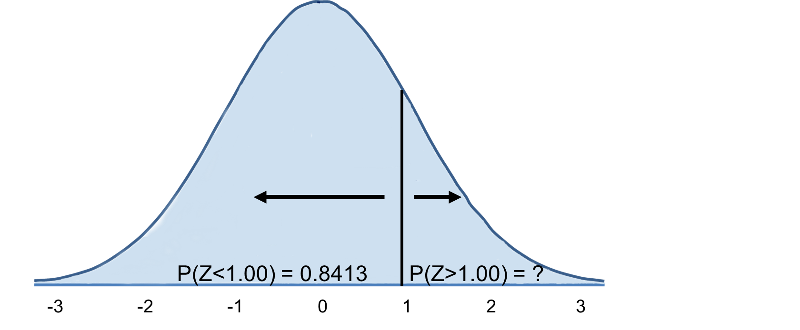
Donc, P(Z>1)=1-0,8413=0,1587. Interprétation : Près de 16% des hommes de 60 ans ont un IMC supérieur à 35.
Calculateur de probabilités normales
![]()
![]()
Z-Scores avec R
Au lieu de chercher les probabilités normales dans le tableau ou d’utiliser Excel, nous pouvons utiliser R pour calculer les probabilités. Par exemple,
> pnorm(0)
Un score Z de 0 (la moyenne de toute distribution) a 50% de la zone à gauche. Quelle est la probabilité qu’un homme de 60 ans dans la population ci-dessus ait un IMC inférieur à 29 (la moyenne) ? Le score Z serait de 0, et pnorm(0)=0,5 ou 50%.
Quelle est la probabilité qu’un homme de 60 ans ait un IMC inférieur à 30 ? Le score Z était de 0,16667.
> pnorm(0,16667)
Donc, la probabilité est de 56,6%.
Quelle est la probabilité qu’un homme de 60 ans ait un IMC supérieur à 35 ?
35-29=6, soit un écart-type au-dessus de la moyenne. Nous pouvons donc calculer la zone à gauche
> pnorm(1)
et soustraire le résultat de 1,0.
1-0,8413447= 0,1586553
Donc la probabilité qu’un homme de 60 ans ait un IMC supérieur à 35 est de 15,8%.
Ou, nous pouvons utiliser R pour calculer le tout en une seule étape comme suit :
> 1-pnorm(1)
Probabilité pour une plage de valeurs

Quelle est la probabilité qu’un homme de 60 ans ait un IMC compris entre 30 et 35 ? Notez que cela revient à demander quelle proportion d’hommes âgés de 60 ans ont un IMC compris entre 30 et 35. Plus précisément, nous voulons P(30 < X < 35) ? Nous avons précédemment calculé P(30<X) et P(X<35) ; comment peut-on utiliser ces deux résultats pour calculer la probabilité que l’IMC soit compris entre 30 et 35 ? Essayez de formuler et de répondre par vous-même avant de regarder l’explication ci-dessous.
Réponse
.