La distribución normal estándar es una distribución normal con una media de cero y una desviación estándar de 1. La distribución normal estándar está centrada en cero y el grado en que una medida dada se desvía de la media viene dado por la desviación estándar. Para la distribución normal estándar, el 68% de las observaciones se sitúan dentro de una desviación estándar de la media; el 95% se sitúan dentro de dos desviaciones estándar de la media; y el 99,9% se sitúan dentro de tres desviaciones estándar de la media. Hasta ahora, hemos utilizado «X» para denotar la variable de interés (por ejemplo, X=IMC, X=altura, X=peso). Sin embargo, al utilizar una distribución normal estándar, utilizaremos «Z» para referirnos a una variable en el contexto de una distribución normal estándar. Después de la estandarización, el IMC=30 discutido en la página anterior se muestra a continuación situándose 0,16667 unidades por encima de la media de 0 en la distribución normal estándar de la derecha.
 ====
====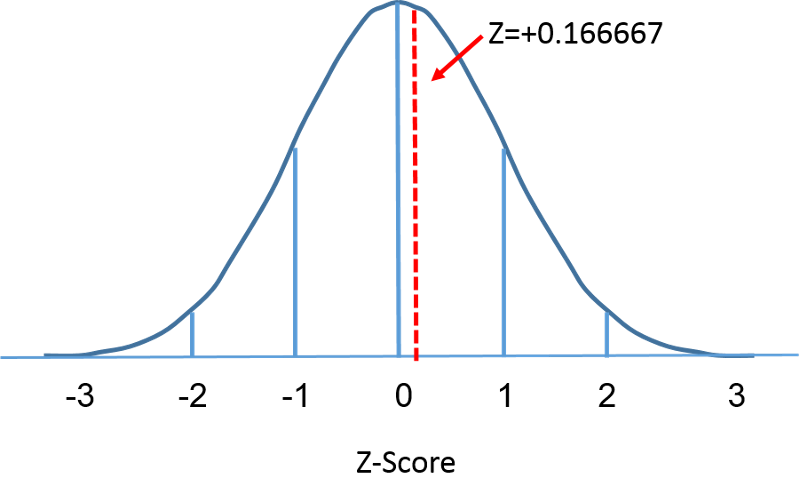
Dado que el área bajo la curva estándar = 1, podemos empezar a definir con más precisión las probabilidades de una observación específica. Para cualquier puntuación Z dada, podemos calcular el área bajo la curva a la izquierda de esa puntuación Z. La tabla del cuadro siguiente muestra las probabilidades para la distribución normal estándar. Examine la tabla y observe que una puntuación «Z» de 0,0 indica una probabilidad de 0,50 o 50%, y una puntuación «Z» de 1, que significa una desviación estándar por encima de la media, indica una probabilidad de 0,8413 o 84%. Esto se debe a que una desviación estándar por encima y por debajo de la media abarca aproximadamente el 68% del área, por lo que una desviación estándar por encima de la media representa la mitad del 34%. Así, el 50% por debajo de la media más el 34% por encima de la media nos da el 84%.
Probabilidades de la distribución normal estándar Z
![]()
Esta tabla está organizada para proporcionar el área bajo la curva a la izquierda de o menos de un valor especificado o «valor Z». En este caso, como la media es cero y la desviación estándar es 1, el valor Z es el número de unidades de desviación estándar que se alejan de la media, y el área es la probabilidad de observar un valor menor que ese valor Z en particular. Observe también que la tabla muestra las probabilidades con dos decimales de Z. El lugar de las unidades y el primer decimal se muestran en la columna de la izquierda, y el segundo decimal se muestra en la fila superior.
Pero volvamos a la pregunta sobre la probabilidad de que el IMC sea inferior a 30, es decir, P(X<30). Podemos responder a esta pregunta utilizando la distribución normal estándar. Las figuras siguientes muestran las distribuciones del IMC para hombres de 60 años y la distribución normal estándar una al lado de la otra.
Distribución del IMC y distribución normal estándar
 ====
====
El área bajo cada curva es una pero la escala del eje X es diferente. Sin embargo, hay que tener en cuenta que las áreas a la izquierda de la línea discontinua son las mismas. La distribución del IMC va de 11 a 47, mientras que la distribución normal estandarizada, Z, va de -3 a 3. Queremos calcular P(X < 30). Para ello, podemos determinar el valor Z que corresponde a X = 30 y, a continuación, utilizar la tabla de distribución normal estandarizada anterior para encontrar la probabilidad o el área bajo la curva. La siguiente fórmula convierte un valor X en una puntuación Z, también llamada puntuación estandarizada:

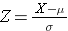
donde μ es la media y σ es la desviación estándar de la variable X.
Para calcular P(X < 30) convertimos la X=30 en su correspondiente puntuación Z (esto se llama estandarizar):

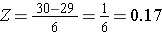
Otro ejemplo
Usando la misma distribución para el IMC, ¿cuál es la probabilidad de que un hombre de 60 años tenga un IMC superior a 35? En otras palabras, ¿cuál es P(X > 35)? De nuevo estandarizamos:

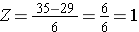
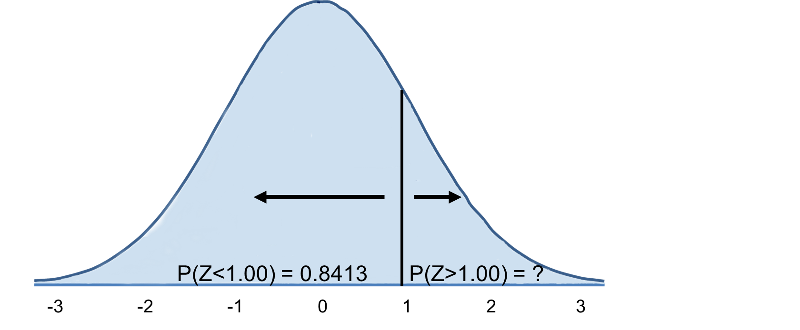
Por tanto, P(Z>1)=1-0,8413=0,1587. Interpretación: Casi el 16% de los hombres de 60 años tienen un IMC superior a 35.
Calculadora de probabilidades normales
![]()
![]()
Puntas Z con R
Como alternativa a la búsqueda de probabilidades normales en la tabla o al uso de Excel, podemos utilizar R para calcular las probabilidades. Por ejemplo,
> pnorm(0)
Una puntuación Z de 0 (la media de cualquier distribución) tiene el 50% del área a la izquierda. ¿Cuál es la probabilidad de que un hombre de 60 años de la población anterior tenga un IMC inferior a 29 (la media)? La puntuación Z sería 0, y pnorm(0)=0,5 o 50%.
¿Cuál es la probabilidad de que un hombre de 60 años tenga un IMC inferior a 30? La puntuación Z era 0,16667.
> pnorm(0,16667)
Así que la probabilidad es del 56,6%.
¿Cuál es la probabilidad de que un hombre de 60 años tenga un IMC superior a 35?
35-29=6, que es una desviación estándar por encima de la media. Así que podemos calcular el área a la izquierda
> pnorm(1)
y luego restar el resultado de 1,0.
1-0,8413447= 0,1586553
Así que la probabilidad de que un hombre de 60 años tenga un IMC superior a 35 es del 15,8%.
O bien, podemos utilizar R para calcular todo en un solo paso de la siguiente manera:
> 1-pnorm(1)
Probabilidad para un rango de valores

¿Cuál es la probabilidad de que un hombre de 60 años tenga un IMC entre 30 y 35? Observe que esto es lo mismo que preguntar qué proporción de hombres de 60 años tienen un IMC entre 30 y 35. En concreto, queremos P(30 < X < 35)? Anteriormente calculamos P(30<X) y P(X<35); ¿cómo se pueden utilizar estos dos resultados para calcular la probabilidad de que el IMC esté entre 30 y 35? Intente formular y responder por su cuenta antes de ver la explicación que aparece a continuación.
Respuesta