De standaardnormale verdeling is een normale verdeling met een gemiddelde van nul en een standaardafwijking van 1. De standaardnormale verdeling is gecentreerd op nul en de mate waarin een gegeven meting afwijkt van het gemiddelde wordt gegeven door de standaardafwijking. Bij de standaardnormale verdeling ligt 68% van de waarnemingen binnen 1 standaardafwijking van het gemiddelde; 95% ligt binnen 2 standaardafwijkingen van het gemiddelde; en 99,9% ligt binnen 3 standaardafwijkingen van het gemiddelde. Tot nu toe hebben we “X” gebruikt om de variabele van belang aan te geven (b.v. X= BMI, X=lengte, X=gewicht). Bij een standaardnormale verdeling zullen wij echter “Z” gebruiken om een variabele in de context van een standaardnormale verdeling aan te duiden. Na standaardisering ligt de op de vorige pagina besproken BMI=30 hieronder 0,16667 eenheden boven het gemiddelde van 0 op de standaardnormale verdeling rechts.
 ====
====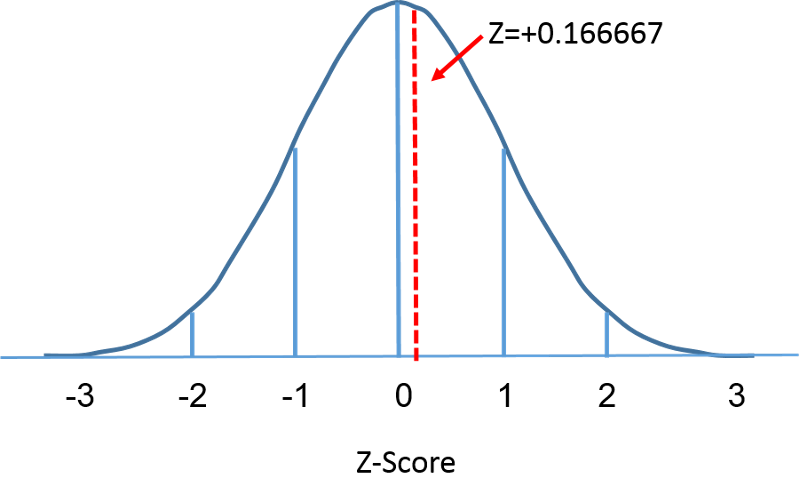
Nadat het gebied onder de standaardkromme = 1, kunnen we de waarschijnlijkheid van specifieke waarnemingen nauwkeuriger gaan bepalen. Voor een gegeven Z-score kunnen wij het gebied onder de kromme links van die Z-score berekenen. De tabel in het kader hieronder toont de waarschijnlijkheden voor de standaardnormale verdeling. Bestudeer de tabel en merk op dat een “Z”-score van 0,0 een kans geeft van 0,50 of 50%, en een “Z”-score van 1, d.w.z. één standaardafwijking boven het gemiddelde, een kans geeft van 0,8413 of 84%. Dat komt omdat één standaardafwijking boven en onder het gemiddelde ongeveer 68% van het gebied beslaat, dus één standaardafwijking boven het gemiddelde vertegenwoordigt de helft daarvan, 34%. Dus, de 50% onder het gemiddelde plus de 34% boven het gemiddelde geeft ons 84%.
Kansen van de Standaardnormale Verdeling Z
![]()
Deze tabel is georganiseerd om het gebied onder de kromme te geven links van of minder dan een bepaalde waarde of “Z-waarde”. In dit geval, omdat het gemiddelde nul is en de standaardafwijking 1, is de Z-waarde het aantal standaardafwijkingseenheden van het gemiddelde verwijderd, en het gebied is de waarschijnlijkheid dat een waarde wordt waargenomen die kleiner is dan die bepaalde Z-waarde. Merk ook op dat de tabel kansen toont tot twee decimalen van Z. De eenheidsplaats en de eerste decimaal staan in de linkerkolom, en de tweede decimaal staat in de bovenste rij.
Maar laten we teruggaan naar de vraag over de waarschijnlijkheid dat de BMI kleiner is dan 30, d.w.z., P(X<30). We kunnen deze vraag beantwoorden met behulp van de standaard normale verdeling. In de onderstaande figuren staan de verdelingen van de BMI voor mannen van 60 jaar en de standaardnormale verdeling naast elkaar.
BMI-verdeling en standaardnormale verdeling
 ====
====
De oppervlakte onder elke kromme is één, maar de schaling van de X-as is verschillend. Merk echter op dat de gebieden links van de stippellijn hetzelfde zijn. De BMI-verdeling loopt van 11 tot 47, terwijl de gestandaardiseerde normale verdeling, Z, loopt van -3 tot 3. We willen P(X < 30) berekenen. Om dit te doen kunnen we de Z-waarde bepalen die overeenkomt met X = 30 en dan de tabel van de standaard normale verdeling hierboven gebruiken om de waarschijnlijkheid of het gebied onder de kromme te vinden. De volgende formule zet een X-waarde om in een Z-score, ook wel gestandaardiseerde score genoemd:

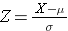
waarbij μ het gemiddelde is en σ de standaardafwijking van de variabele X.
Om P(X < 30) te berekenen, zetten we X=30 om in de bijbehorende Z-score (dit heet standaardiseren):

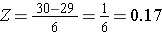
Een ander voorbeeld
Gebruik makend van dezelfde verdeling voor BMI, wat is de kans dat een man van 60 een BMI heeft die hoger is dan 35? Met andere woorden, wat is P(X > 35)? Opnieuw standaardiseren we:

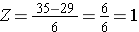
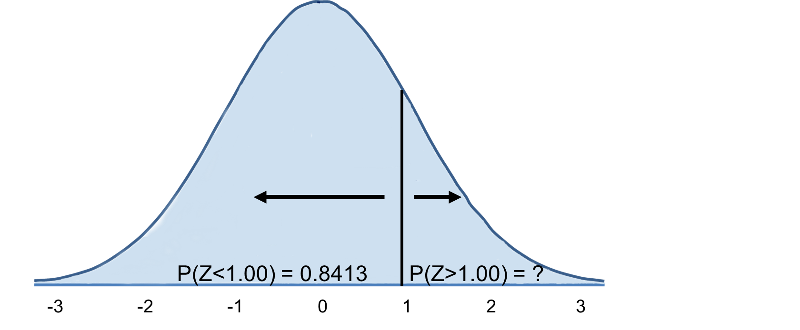
Daaruit volgt P(Z>1)=1-0,8413=0,1587. Interpretatie: Bijna 16% van de mannen van 60 jaar heeft een BMI van meer dan 35.
Normale waarschijnlijkheidsberekenaar
![]()
![]()
Z-Scores met R
Als alternatief voor het opzoeken van normale waarschijnlijkheden in de tabel of met Excel, kunnen we R gebruiken om waarschijnlijkheden te berekenen. Bijvoorbeeld,
> pnorm(0)
Een Z-score van 0 (het gemiddelde van een verdeling) heeft 50% van het gebied aan de linkerkant. Hoe groot is de kans dat een 60-jarige man in de bovenstaande populatie een BMI heeft die lager is dan 29 (het gemiddelde)? De Z-score zou 0 zijn, en pnorm(0)=0.5 of 50%.
Wat is de kans dat een 60-jarige man een BMI heeft die lager is dan 30? De Z-score was 0,16667.
> pnorm(0,16667)
De kans is dus 56,6%.
Wat is de kans dat een 60-jarige man een BMI heeft die groter is dan 35?
35-29=6, dat is één standaardafwijking boven het gemiddelde. We kunnen dus het gebied links daarvan berekenen
> pnorm(1)
en dan het resultaat van 1,0 aftrekken.
1-0,8413447= 0,1586553
Dus de kans dat een 60-jarige man een BMI heeft die hoger is dan 35 is 15,8%.
Of we kunnen R gebruiken om het geheel in één stap als volgt te berekenen:
> 1-pnorm(1)
Kans voor een bereik van waarden

Wat is de kans dat een man van 60 jaar een BMI tussen 30 en 35 heeft? Merk op dat dit hetzelfde is als de vraag welk deel van de mannen van 60 jaar een BMI tussen 30 en 35 heeft. Specifiek willen we P(30 < X < 35)? We hebben eerder P(30<X) en P(X<35) berekend; hoe kunnen deze twee resultaten worden gebruikt om de kans te berekenen dat de BMI tussen 30 en 35 ligt? Probeer zelf een antwoord te formuleren en te geven voordat je naar de uitleg hieronder kijkt.
Antwoorden