Grundlagen des Kondensators, Funktionsweise und verschiedene Arten von Kondensatoren mit ihren Anwendungen in Schaltkreisen

Kondensatoren – das Wort scheint die Vorstellung von Kapazität zu suggerieren, was laut Wörterbuch „die Fähigkeit, etwas zu halten“ bedeutet. Genau das tut ein Kondensator – er speichert elektrische Ladung. Aber was macht ihn zu einem gängigen Bauteil in fast allen elektronischen Schaltungen? In diesem Artikel wollen wir die Funktionsweise von Kondensatoren aufschlüsseln, um zu verstehen, was sie tun und wie man sie verwenden kann.

Was ist ein Kondensator?

Ein Kondensator in seiner primitivsten Form besteht aus zwei leitenden Platten, die durch ein Dielektrikum getrennt sind. Der Begriff Dielektrikum ist nur ein schickes Wort für einen Isolator, der polarisiert werden kann, d.h. negative und positive Ladungen auf gegenüberliegenden Seiten bilden kann. Wenn eine Spannung an diese beiden Platten angelegt wird, fließt Strom durch die leitenden Platten. Eine Seite wird positiv geladen (Elektronenmangel) und die andere Seite wird negativ geladen (Elektronenüberschuss). Wir alle kennen die Tatsache, dass sich ungleiche Ladungen anziehen. Da die Platten also entgegengesetzt geladen sind, ziehen sich die Ladungen auf den Platten an.

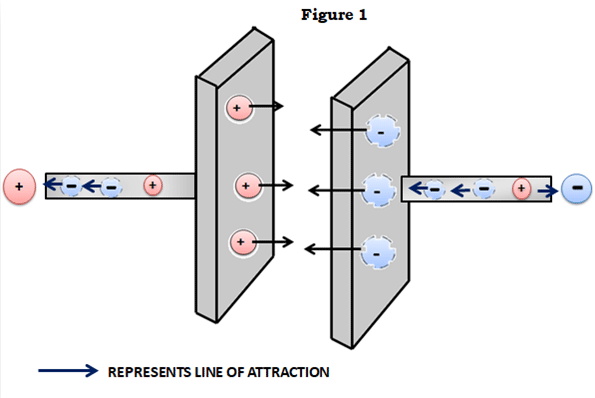
Da sich zwischen den Platten ein Isolator befindet, können die Ladungen nicht „fließen“, um sich gegenseitig auszugleichen, sondern bleiben (im Idealfall) in einem Zustand gegenseitiger Anziehung stecken. Auf diese Weise erfüllen Kondensatoren ihre grundlegendste Funktion – das Zurückhalten oder Speichern von Ladung.

Symbol für Kondensatoren

Da Kondensatoren, wie oben beschrieben, zwei parallele Metallplatten haben, stellt ihr Symbol gewissermaßen dasselbe dar. Zumindest ist es leicht zu zeichnen

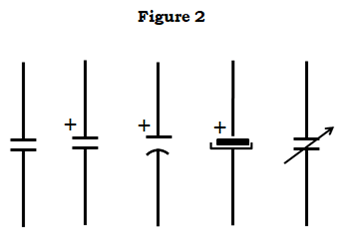
Im praktischen Fall sind Kondensatoren nicht mehr nur zwei Platten mit einem Spalt dazwischen, bei Aluminium-Elektrolytkondensatoren haben die beiden Platten die Form einer Metallfolie, die mit einem Abstandshalter dazwischen in einer Röhre aufgerollt ist.

Die zweite Gruppe von Symbolen steht für gepolte Kondensatoren, d.h. solche, die durch den internen Aufbau definierte positive und negative Anschlüsse haben. Ein versehentliches Vertauschen dieser Anschlüsse führt mit ziemlicher Sicherheit zu einem spektakulären Ausfall (vor allem bei größeren Exemplaren), bei dem Folienstücke und Papiermeter aus der Ausfallstelle herausgeschleudert werden und die meiste Zeit sehr übel riechen.

Kapazität und Spannungswert eines Kondensators

Kondensatoren werden in Farad gemessen; sie ist nach dem berühmten britischen Elektrochemiker Michael Faraday benannt. Die Einheit der Kapazität, die für Coulomb pro Volt steht. Das Coulomb (ausgesprochen ‚koo-lom‘) ist die SI-Einheit für Ladung, und ein Volt ist, wie wir wissen, die Einheit für Spannung oder Potenzialdifferenz. Somit ist das Farad die Menge der gespeicherten Ladung pro Volt Potentialdifferenz. Diese einfache Art, einen Kondensator mathematisch zu betrachten, bietet eine Vielzahl von Interpretationsmöglichkeiten, die sich in einer Menge tödlich komplexer mathematischer Gleichungen wie Integralen, Exponenten und Vektoren manifestieren, die wir Ingenieure bei der Arbeit mit Kondensatoren verwenden. Wir werden uns jedoch im weiteren Verlauf des Artikels mit ein wenig interessanter Mathematik befassen, die uns beim Entwurf von Schaltungen mit Kondensatoren helfen wird

Natürlich ist das Farad (ein Coulomb pro Volt) für die meisten praktischen Zwecke eine sehr große Einheit (da das Coulomb selbst eine ziemlich große Ladungsmenge ist, wie du vielleicht schon weißt), daher werden die meisten Kondensatoren (außer sehr großen) in Mikrofarad gemessen, oder einem Millionstel (0,000001) eines Farad. Nehmen wir an, Sie haben einen Kondensator mit der Angabe 25V 10uF (das Präfix „u“ steht für Mikro, eine Verballhornung des griechischen Symbols µ („mu“), das „Mikro“ bedeutet) auf der Kunststoffhülle. Da die Kappe (in der Elektronikwelt kurz für Kondensatoren) für 10uF ausgelegt ist, kann sie eine Ladung von zehn Mikro-Coulombs (d. h. zehn Millionstel eines Coulomb, 0,000010 C) pro Volt Spannung an ihren Anschlüssen halten. Das bedeutet, dass der Kondensator bei der maximalen Spannung von 25 V eine Ladung von 25 V x 10 uF aufnehmen kann, was 0,000250 Coulomb entspricht.

Erinnern Sie sich daran, dass ich „maximale“ Spannung sagte. Die maximale Spannung ist wahrscheinlich der wichtigste Wert auf dem Kondensator. Sie gibt an, wie viel Spannung ein Kondensator an seinen Anschlüssen verkraften kann, bevor er KABOOM………!

Arbeitsweise eines Kondensators

Grundsätzlich passiert in einem Kondensator, dass der Isolator zwischen den Platten einen Prozess durchläuft, der „dielektrischer Durchbruch“ genannt wird, d.h. der Isolator kann nicht mehr isolieren, da die Spannung über dem Isolator zu hoch ist, als dass er ein Isolator bleiben könnte. Die zugrundeliegende Physik ist nicht ganz klar, aber alles, was Sie wissen müssen, um zu verstehen, warum dies geschieht, ist, dass kein Isolator perfekt ist, d. h. bis zu einem bestimmten Punkt. Selbst die stärkste Brücke bricht zusammen, wenn sie überlastet wird. Was hier passiert, ist ähnlich. Um den Durchbruch zu verringern, könnte man den Abstand zwischen den beiden Platten vergrößern, aber das bringt einen Nachteil mit sich – eine geringere Kapazität, da die Platten weiter voneinander entfernt sind und sich die Ladungen nicht so stark anziehen, wie sie es tun, wenn sie näher beieinander liegen – ähnlich wie bei Magneten.

Eine gute Faustregel wäre, Kappen zu verwenden, die für eine 50 % höhere Spannung ausgelegt sind als die, die in Ihrer Schaltung zu erwarten ist. Das lässt einen großen Sicherheitsspielraum. Wenn du zum Beispiel einen Kondensator brauchst, um eine 12-V-Stromversorgungsschiene zu entkoppeln (keine Sorge, das Entkoppeln wird später im Artikel erklärt), könntest du mit einem 16-V-Kondensator auskommen, aber es wird empfohlen, einen 25-V-Kondensator zu verwenden, da er dir eine große Sicherheitsmarge bietet. Okay, du hast es herausgefunden! Ja, 25 V ist natürlich nicht 25 % mehr als 12 V, aber 18 V ist kein Standardkondensatorwert – Sie werden keinen mit diesem Spannungswert finden. Der nächstgelegene Wert ist 25V.

Unterschiedliche Arten von Kondensatoren

Der Grund für die unterschiedlichen Durchbruchsspannungsbereiche liegt im Material, das als Dielektrikum verwendet wird, was auch die Grundlage für die Klassifizierung von Kondensatoren ist:

Aluminium-Elektrolytkondensatoren

Diese sind wahrscheinlich die am besten erkennbaren Arten von Kondensatoren. Sie werden in charakteristischen Metalldosen mit Kunststoffummantelung geliefert, mit klar angegebenen Spannungs- und Kapazitätswerten und einem weißen Band zur Kennzeichnung der Kathode. Der Name kommt daher, dass die „Platten“, wie oben erwähnt, aus chemisch geätzter Aluminiumfolie bestehen. Durch das Ätzen wird das Aluminium porös (ähnlich wie ein Schwamm) und vergrößert seine Oberfläche erheblich, wodurch sich die Kapazität erhöht. Das Dielektrikum ist eine dünne Schicht aus Aluminiumoxid. Diese Kondensatoren sind mit Öl gefüllt, das wie ein Elektrolyt wirkt, daher der Name. Elektrolytkondensatoren sind aufgrund ihres inneren Aufbaus gepolt. Sie haben im Vergleich zu anderen Kondensatoren eine große Kapazität, aber eine viel geringere Spannung. Man findet Elektrolytkondensatoren mit Kapazitäten von 0,1uF bis zu 100mF und Nennspannungen von einigen Volt bis zu etwa 500V. Ihre Innenwiderstände sind jedoch in der Regel hoch.

Seitliche Anmerkung: Der Innenwiderstand von Kondensatoren ist auf die Materialien zurückzuführen, aus denen der Kondensator besteht – zum Beispiel der Widerstand der Aluminiumfolie oder der Widerstand der Leitungen.

Keramikkondensatoren

Das sind Kondensatoren mit einem Keramikdielektrikum. Da die Durchschlagsgrenze für das keramische Dielektrikum recht hoch ist, kann man Keramikkondensatoren mit verrückten Durchschlagsspannungen wie 10 kV erwarten. Die Kapazität ist jedoch eher gering und liegt im Bereich von Picofarad (0,000000000001F) bis zu einigen zehn Mikrofarad. Sie sind im Allgemeinen viel kleiner als andere Arten von Kondensatoren, wie auf dem Bild zu sehen ist. Sie haben auch sehr kleine Innenwiderstände.

Keramikkondensatoren identifizieren

Der Wert einer Keramikkapazität wird nicht direkt auf dem Keramikkondensator angegeben. Es gibt immer eine dreistellige Zahl, gefolgt von einer Variablen; lernen wir, wie man den Wert anhand dieser Zahlen identifiziert. Betrachten wir den folgenden Kondensator:

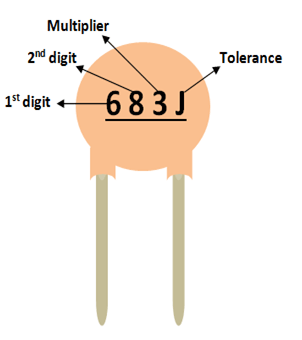
Wie Sie feststellen können, sind diese drei Ziffern in zwei Ziffern aufgeteilt und die dritte ist der Multiplikator. In diesem Fall ist 68 die Ziffer und 3 ist der Multiplikator. 68 sollte also mit 10^3 multipliziert werden. Einfach ausgedrückt ist das 68 gefolgt von 3 Nullen. Der Wert dieses Kondensators ist also 68000 pF. Beachten Sie, dass die Einheit immer pF sein sollte. In ähnlicher Weise bedeutet ein Kondensator mit dem Code 220, dass er 22 Pico-Farad hat, da 10^0 gleich 0 ist.

Die Nennspannung des Kondensators lässt sich anhand der Linie unter diesem Code ermitteln. Wenn es eine Linie gibt, dann ist der Spannungswert 50/100V, wenn es keine Linie gibt, dann ist es 500V.

Die am häufigsten verwendeten Kondensatorwerte zusammen mit ihrer Umwandlung in Pico Farad, Nano Farad und Mikrofarad sind unten angegeben.

Folienkondensatoren

Wie der Name schon sagt, ist das Dielektrikum in diesen Kondensatoren eine Kunststofffolie, oft bekannte Kunststoffe wie Mylar und Polyester. Sie haben die gleichen Eigenschaften wie Keramikkondensatoren, nämlich hohe Durchbruchsspannungen (wegen des Verhaltens der Kunststoffpolymere) und niedrige Kapazitäten. Der einzige Unterschied besteht darin, dass sie in der Regel etwas größer sind, obwohl sie oberflächlich betrachtet wie Keramikkappen aussehen. Der Innenwiderstand ist mit dem von Keramikkondensatoren vergleichbar.

Tantal- und Niobkondensatoren

Diese Kondensatoren fallen technisch gesehen unter die Kategorie der Elektrolytkondensatoren. Der Elektrolyt ist hier ein festes Material aus Tantal- oder Nioboxiden. Sie haben einen sehr niedrigen Innenwiderstand für eine gegebene Kapazität, sind aber im Vergleich zu anderen Typen weniger immun gegen Überspannungen (Keramik hat die besten) und neigen dazu, ohne große Vorwarnung und mit viel unangenehmem schwarzem Rauch kaputt zu gehen.

Spezialkondensatoren

Dazu gehören Silber-Glimmer-Kondensatoren, X- und Y-Kondensatoren usw. X- und Y-Kondensatoren werden z. B. für die Netzfilterung gebaut – robustere Konstruktion und höhere Spannungswerte, aber auch niedrige Kapazitäten, um den Strom zu reduzieren, der durch den Kondensator fließt, wenn Wechselspannung anliegt, und um die im Kondensator gespeicherte Energie zu begrenzen, wenn Gleichspannung anliegt.

Superkondensatoren und Ultrakondensatoren

Sie heben Kondensatoren auf eine ganz neue Ebene, mit stark erhöhten Kapazitäten, manchmal im Bereich von Hunderten von Farad! Möglich wird dies durch eine ausgeklügelte Chemie. Superkondensatoren und Ultrakondensatoren schließen die Lücke zwischen Kondensatoren und chemischen Batterien. Es gibt sie allerdings mit sehr niedrigen Spannungen.

Und das sind so ziemlich alle gängigen Arten von Kondensatoren, denen man in der Welt der Elektronik begegnen kann.

Wie sich Kondensatoren in Schaltkreisen verhalten

Eine nützliche erste Aufgabe wäre zu lernen, wie man die in einem Kondensator gespeicherte Energie berechnet, die durch die Formel,

E = 1/2CV2

gegeben wird, wobei E die gespeicherte Energie in Joule, C die Kapazität in Farad und V die Spannung in Volt ist. Man beachte, dass diese Gleichung die Form vieler anderer Newton’scher Gleichungen für Energie annimmt, ein nettes Osterei!

Angenommen, man hat einen Kondensator, der für eine Spannung von 50V ausgelegt ist und eine Kapazität von 1000uF hat, dann wäre die gespeicherte Energie bei den vollen 50V:

1/2 * 0.001000F * 50V * 50V

Das sind schlappe 1,25J gespeicherte Energie.

Dies zeigt einen großen Nachteil von Kondensatoren als Energiespeicher – die gespeicherte Energie für eine gegebene Größe ist sehr gering, eine Batterie der gleichen Größe hätte mindestens tausendmal mehr gespeicherte Energie! Allerdings haben Kondensatoren einen wesentlich geringeren Innenwiderstand als chemische Batterien, so dass sie ihre gesamte gespeicherte Energie schnell abgeben können. Ein Kurzschluss bei einer Batterie würde nur dazu führen, dass sie sich aufgrund der durch den Innenwiderstand abgeleiteten Energie erwärmt, aber ein Kurzschluss bei einem Kondensator würde nur ein paar Funken erzeugen, da die gesamte Ladung auf einmal entladen wird, ohne den Kondensator zu beschädigen.

Zweitens gibt es eine weitere nette Formel, die Spannung, Strom und Kapazität in Beziehung setzt:

I/C = dV/dt

Wobei I der dem Kondensator zugeführte Strom in Ampere ist, C die Kapazität in Farad und dV/dt die Änderungsrate der Spannung an den Kondensatoranschlüssen ist. Stellen Sie sich dies als Einheit vor – Volt pro Sekunde bei einem bestimmten Strom und einer bestimmten Kapazität. Mach dir keine Gedanken über das kleine ‚d‘, es ist nur eine mathematische Art zu sagen ‚bis zum Grenzwert Null‘.

Angenommen, du hast eine Stromversorgung, die eine konstante Spannung von 5V bei einem konstanten Strom von 1mA ausgibt, dann können wir durch Umstellen der Gleichung die Zeit finden, die benötigt wird, um einen 100uF Kondensator auf 5V aufzuladen:

dt = CdV/I

dt = (0.000100F * 5V)/0.001A

dt = 0.5 Sekunden

Der Kondensator würde sich also in 0.5 Sekunden auf 5V aufladen. (Denken Sie daran, dass ein Kondensator sich nur bis zur maximalen Spannung aufladen kann, die ihm zugeführt wird, niemals mehr, er kann nicht auf magische Weise Spannung „erzeugen“.)

Dieses vorhersehbare Verhalten eines Kondensators macht ihn sehr nützlich, um z. B. mit einem kleinen zusätzlichen Schaltkreis Zeitverzögerungen zu erzeugen. Man kann die Gleichung umstellen, um die Zeit zu erhalten.

Nun zum Wesentlichen – den Kondensatorschaltungen!

Verhalten von Kondensatoren in Schaltungen

Fangen wir ganz einfach an – mit den verschiedenen Möglichkeiten, wie Kondensatoren miteinander verbunden werden können. Sie können entweder in Reihe oder parallel geschaltet werden.

Parallel geschaltete Kondensatoren

Die folgende Abbildung zeigt drei parallel geschaltete Kondensatoren, deren Plus- und Minuspole miteinander verbunden sind (vorausgesetzt, die Kondensatoren sind gepolt). Die Gesamtkapazität dieser Anordnung ist einfach die Summe aller Kapazitäten aller Kondensatoren in der Schaltung. Das ist sinnvoll, da die Parallelschaltung der Kondensatorplatten die Oberfläche vergrößert und damit die Kapazität erhöht.

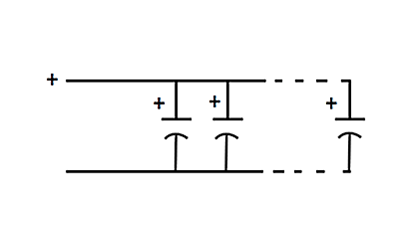
Die maximale Spannung, die eine solche Anordnung verkraften kann, ist die Spannung des kleinsten Kondensators, da die Spannung für alle Kondensatoren gleich ist.

Ein Beispiel soll dies verdeutlichen. Nehmen wir an, Sie haben zwei Kondensatoren, einer mit den Werten 25V 470uF und der andere 35V 1000uF. Die Gesamtkapazität wäre dann 470uf + 1000uF = 1470uF. Die maximale Spannung, die Sie an diese Bank anlegen können (eine Reihe zusammengeschalteter Kondensatoren kann als Kondensator-„Bank“ bezeichnet werden), beträgt jedoch nur 25 V. Wenn man etwas Höheres über diese Bank legt, würden Funken fliegen, da man die maximale Spannung des 25-V-Kondensators überschreitet.

Kondensatoren in Reihe schalten

Eine Parallelschaltung von Kondensatoren ist besonders nützlich, wenn man eine große Kapazität wünscht und nur kleine Werte hat. Wenn man die kleineren Werte parallel schaltet, erhält man schließlich den größeren Wert und kann die Aufgabe erfüllen, vorausgesetzt, man achtet auf die Spannung.

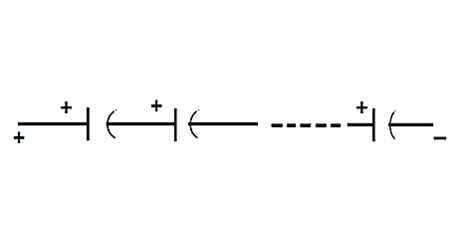
Nun ist die Reihenschaltung von Kondensatoren etwas komplizierter. Die Kapazität ergibt sich aus der Formel:

1/Gesamt = 1/C1 + 1/C2 + … + 1/Cn

Wobei C1, C2…Cn die Kapazitäten der einzelnen in der Schaltung verwendeten Kondensatoren sind.

Die Spannung, die die Bank jetzt verarbeiten kann, ist die Summe aller Nennspannungen.

Wenn man einen Kondensator mit einer Nennspannung von 10V 1uF und einen Kondensator mit einer Nennspannung von 50V 10uF hat, dann ist die Spannung, die die Bank in Reihe schalten kann, 10V + 50V = 60V. Die Kapazität beträgt 0,9091uF.

Kondensatorspannung im Verhältnis zur Zeit

Was, wenn wir einen Kondensator aufladen wollen? Wir könnten ihn einfach an eine Spannungsquelle anschließen, wie in der Abbildung unten. In dem Moment, in dem die Spannungsquelle angeschlossen wird und der Kondensator vollständig entladen ist, sammeln sich Ladungen auf den Platten an, was zu einer sehr großen (theoretisch unendlichen!) Stromspitze führt, die nur durch den Innenwiderstand des Kondensators begrenzt wird. Dies ist natürlich nicht erwünscht, wenn die Stromversorgung über eine Batterie erfolgt. Eine vernünftige Idee wäre es, einen Widerstand in Reihe mit dem Kondensator und der Spannungsquelle zu schalten, um den Strom wie in der Abbildung zu begrenzen, und voila! Sie haben etwas, das die Ingenieure als RC-Schaltung bezeichnen, ‚R‘ für Widerstand und ‚C‘ für Kondensator!

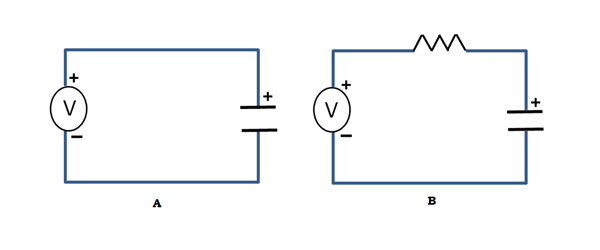
Diese Schaltung zeigt ein interessantes Verhalten. Wenn die Spannung an der mit ‚I‘ bezeichneten Seite des Widerstands angeschlossen wird, steigt die Spannung am Kondensator langsam an, da der Strom begrenzt ist. Das Diagramm sieht in etwa so aus:

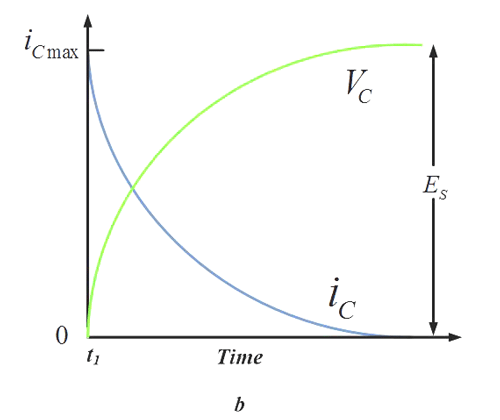
Die mathematisch begabteren unter meinen Zuschauern werden die Form der Steigung erkennen – sie ähnelt der einer Exponentialfunktion!

Erinnern Sie sich, wie ich sagte, dass man mit Kondensatoren Zeitverzögerungen erzeugen kann? Dies ist eine Möglichkeit, dies ohne eine Konstantstromquelle zu tun (was einige zusätzliche Schaltungen erfordert). Da die Zeit, die benötigt wird, um eine bestimmte Spannung zu erreichen, vorhersehbar ist, wenn wir die Kapazität, die Spannung und den Widerstand kennen, können wir Zeitverzögerungsschaltungen erstellen.

Das Produkt aus Widerstand und Kapazität, RC, ist als die Zeitkonstante der Schaltung bekannt. Dieser Parameter ist nützlich, um die Zeit bis zum Erreichen einer bestimmten Spannung genau zu bestimmen, wie das folgende Diagramm zeigt.

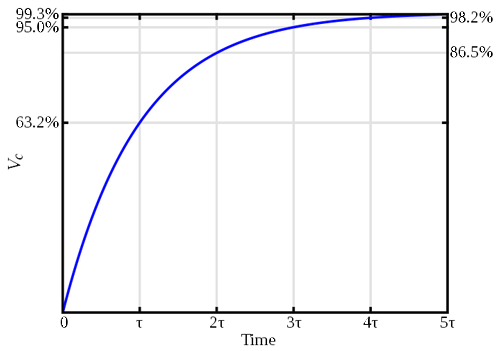
Aus dem Diagramm kann man ersehen, dass der Kondensator 63% der angelegten Spannung in einer Zeitkonstante erreicht, und so weiter.

Dies ist das Prinzip, das der ganzjährige 555-Timer verwendet, obwohl die Konstruktionsgleichungen ein wenig anders sind.

Eine weitere interessante Anwendung von RC-Schaltungen ist die Signalfilterung, d.h. die Entfernung eines elektrischen Signals einer unerwünschten Frequenz aus einem Schaltkreis. Der RC-Stromkreis benötigt eine bestimmte Zeit, um sich von einer Quelle aufzuladen und zu entladen. Legt man eine periodische Welle mit einer Zeitspanne größer als RC an, so erscheint das gleiche Signal am Ausgang mit sehr geringer Verzerrung. Erhöht man jedoch die Frequenz, ändert sich die Polarität des Signals schneller, als die Schaltung laden und entladen kann, und ab einem bestimmten Punkt verschwindet das Signal, und man hat nur noch reinen Gleichstrom! Dies wird als Signaldämpfung bezeichnet. Wie Sie sehen, wirkt ein RC-Stromkreis wie ein Filter, der Wechselstromsignale (auch solche, die mit Gleichstrom überlagert sind, d. h. einen Gleichstrom-Offset haben) ab einer bestimmten Frequenz blockiert. Diese Art von Filter wird als Tiefpassfilter bezeichnet, d.h. er lässt niedrige Frequenzen durch, aber keine hohen Frequenzen.

Kondensatoren in Wechselstromkreisen

Kondensatoren verhalten sich auf interessante Weise, wenn sie in Wechselstromkreisen eingesetzt werden. Man kann sie als frequenzabhängige Widerstände betrachten, vom Standpunkt des Signals aus gesehen. Wie oben gesehen, sperrt der RC-Kreis den gesamten Wechselstrom eines Signals, aber was passiert, wenn ein Kondensator in Reihe mit einer Wechselspannungsquelle geschaltet wird? Das genaue Gegenteil!

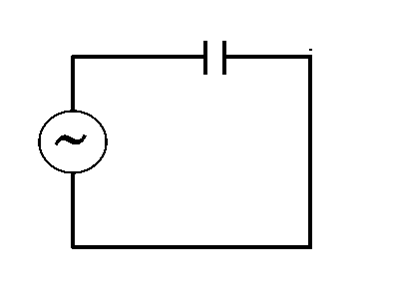
Da der Kondensator nur aus zwei durch einen Isolator getrennten Metallplatten besteht, lässt er keinen Gleichstrom durch. Ein Wechselstromsignal hat jedoch ständig wechselnde Spannungen, so dass eine Platte eine wechselnde Spannung erfährt und die entgegengesetzte Ladung auf der anderen Platte induziert, wie in der Abbildung gezeigt:

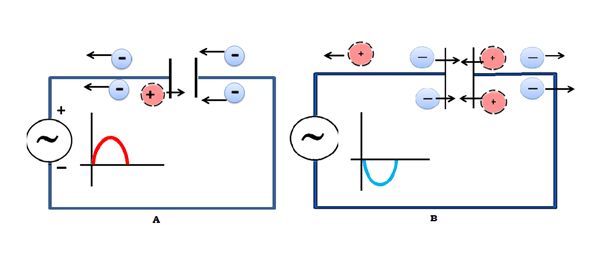
Dies hat den allgemeinen Effekt, dass Strom bei relativ hohen Frequenzen durch den Kondensator „fließt“. Die Hinzufügung eines Widerstands parallel zum Ausgang ergibt einen Hochpassfilter, d. h. einen Filter, der nur hohe Frequenzen durchlässt und alle Gleichstromsignale sperrt.

Der „Wechselstromwiderstand“ oder die Impedanz eines Kondensators wird durch die folgende Formel angegeben:

XC = 1/(2*π*f*C)

Wobei XC der kapazitive Blindwiderstand oder die Impedanz, f die Frequenz und C die Kapazität ist. Mit dieser Formel kann man den virtuellen „Widerstand“ berechnen, den ein Kondensator in einem Wechselstromkreis hat.

Wo man Kondensatoren in der Natur findet

Okay, das war genug Theorie. Schauen wir uns die vielen Verwendungsmöglichkeiten von Kondensatoren an.

Der erste Ort, an dem man Kondensatoren erwarten würde, sind Stromversorgungen aller Art als Filter und zur Entkopplung. Sie dienen als Ladungsspeicher und liefern schnellen Strom, wenn die Last ihn braucht.

Hier sind zwei Oszilloskop-Aufnahmen, die die Auswirkungen eines fehlenden und eines vorhandenen Kondensators an den Leitungen eines Netzteils zeigen. Wie Sie sehen können, reduzieren Kondensatoren das „Rauschen“ auf den Stromversorgungsschienen drastisch und schützen so empfindliche Teile vor plötzlichen Spannungsspitzen.

Sie werden auch „Entkopplungskondensatoren“ genannt, da sie Teile der Schaltung, über die sie montiert sind, von der Stromversorgung „entkoppeln“. Manchmal sind die Stromzuführungen auf einer Leiterplatte recht lang und haben eine hohe Induktivität und einen hohen Widerstand. Dies kann dazu führen, dass sie weniger Strom als üblich liefern. Ein Kondensator am Ende der Stromversorgungsleitung ist wie eine kleinere, vorübergehende „Batterie“ über dem Gerät, die bei Bedarf Stromstöße liefert und sich auflädt, wenn das Gerät wenig Strom verbraucht.

Sie können die Formel I/C = dV/dt verwenden, um die erforderliche Kapazität zu berechnen, um die „Brummspannung“ von den Stromversorgungsanschlüssen zu entfernen.

Angenommen, Sie haben eine Stromversorgung, deren Spannung alle 10 ms von 11,5 V auf 12 V (Welligkeit) schwankt, was bei netzbetriebenen Geräten aufgrund der 50 Hz-Frequenz üblich ist, und Sie müssen eine Kappe über die Klemmen legen, um die Spannung zu glätten. Wenn der Laststrom in diesem Fall 1 A beträgt, können wir die Formel wie folgt umstellen, um die Kapazität zu ermitteln:

(I * dt)/dV

Wobei I der Laststrom, dt die Zeitdauer des Rauschens und dV die Brummspannung ist. Setzt man die Werte ein, so ergibt sich, dass wir eine Kapazität von 20000uF benötigen. Das mag viel erscheinen, aber man kann auch mit viel weniger auskommen. Der ermittelte Wert dient nur als Richtwert.

Im wirklichen Leben findet man oft mehrere Arten und Werte von Kondensatoren auf den Leiterbahnen, um den Rauschanteil über viele Frequenzen zu reduzieren und eine möglichst glatte Spannung zu erhalten.

Eine andere Verwendung von Kondensatoren sind komplizierte Filter wie dieser:

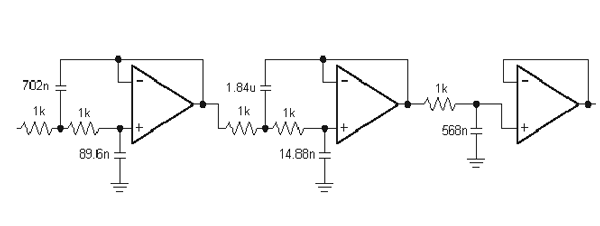
Ein einfacheres Filter ist das RC-Filter, ein interessantes Filter wird hier beschrieben.

Jeder kennt das Arduino Mikrocontroller-Board. Ein vielseitiges Werkzeug, aber haben Sie sich nicht schon einmal gefragt, warum die analogen Ausgänge ein digitales PWM-Signal ausspucken? Das liegt daran, dass sie für die Verwendung mit einem externen Filternetzwerk konzipiert wurden, um die PWM-Spannung zu einer echten Analogspannung zu glätten. Dies kann mit so einfachen Teilen wie einem 1K-Widerstand und einem 10uF-Kondensator geschehen. Probieren Sie es aus!

Eine andere Verwendung ist, wie oben erwähnt, die Zeitmessung. Ein einfacher Oszillator kann mit einem NAND-Gatter (versuche herauszufinden, warum AND-Gatter nicht funktionieren), einem Widerstand und einem Kondensator gebaut werden.

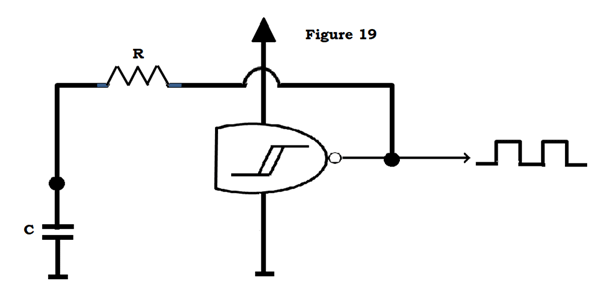
Angenommen, dass anfangs keine Spannung über dem Kondensator anliegt, sehen die NAND-Eingänge (die miteinander verbunden sind) fast 0V über ihnen und schalten den Ausgang ein. Der Kondensator lädt sich nun über den Widerstand auf. Wenn er den „High“-Schwellenwert des Gatters erreicht, schaltet der Ausgang auf Low und der Kondensator entlädt sich. Dieser Zyklus setzt sich fort und erzeugt eine Rechteckwelle mit einer Frequenz, die von den Werten von R und C abhängt.

Eine weitere interessante Verwendung von Kondensatoren ist die Energiespeicherung. Natürlich können Kondensatoren nicht mit Batterien mithalten, aber für einige Anwendungen, bei denen die Energie schnell benötigt wird, sind Kondensatoren am besten geeignet.

Geräte wie Spulenkanonen (mehr dazu im Internet) benötigen einen großen Stromimpuls, um das Projektil zu beschleunigen, daher werden für solche Zwecke Hochspannungskondensatoren verwendet, oft mit Werten wie 450V 1500uF, die erhebliche Energiemengen speichern können.