
Pflanzen können neue Zellen in Spiralen wachsen lassen, wie das Muster der Samen in dieser schönen Sonnenblume.
Die Spirale entsteht auf natürliche Weise, weil jede neue Zelle nach einer Drehung gebildet wird.
„Neue Zelle, dann Drehung,
dann noch eine Zelle, dann Drehung, …“
Wie weit soll man sich drehen?
Wenn du also eine Pflanze wärst, wie weit würdest du dich zwischen neuen Zellen drehen?
Wenn du dich überhaupt nicht drehst, bekommst du eine gerade Linie.
![]()
Aber das ist ein sehr schlechtes Design …. du willst etwas Rundes, das ohne Lücken zusammenhält.
Warum nicht versuchen, den besten Wert für dich zu finden?
Versuch verschiedene Werte, wie 0,75, 0,9, 3,1416, 0,62, usw.
Vergiss nicht, dass du versuchst, ein lückenloses Muster vom Anfang bis zum Ende zu erstellen:
(Übrigens spielt es keine Rolle, ob es sich um ganze Zahlen handelt, wie z.B. die 1 oder die 5, denn es sind volle Umdrehungen, die in die gleiche Richtung zurückführen.)
Was hast du bekommen?
Wenn du etwas bekommen hast, das wie 0,618 endet (oder 0,382, was 1 – 0,618 ist), dann „Herzlichen Glückwunsch, du bist ein erfolgreiches Mitglied des Pflanzenreichs!“
 |
Das liegt daran, dass der Goldene Schnitt (1.61803…) die beste Lösung ist, und die Sonnenblume hat dies auf ihre eigene natürliche Weise herausgefunden. Versuchen Sie es … es sollte so aussehen. |
Warum?
Jede Zahl, die ein einfacher Bruch ist (Beispiel: 0.75 ist 3/4, und 0,95 ist 19/20, usw.), wird nach einer Weile ein Muster von Linien bilden, die sich übereinander stapeln, wodurch Lücken entstehen.
Aber der Goldene Schnitt (sein Symbol ist der griechische Buchstabe Phi, links abgebildet) ist ein Experte darin, kein Bruch zu sein.
Er ist eine irrationale Zahl (was bedeutet, dass wir ihn nicht als einfachen Bruch schreiben können), aber mehr als das … er ist so weit davon entfernt, ein Bruch zu sein, wie wir es nur können.
| Eine irrationale Zahl zu sein, reicht nicht aus | |
|---|---|
 |
Pi (3,141592654…), das ebenfalls irrational ist. Dummerweise hat es einen Dezimalwert, der sehr nahe bei 1/7 liegt (= 0,142857…), so dass es mit 7 Armen endet. |
 |
e (2,71828…), das ebenfalls irrational ist, funktioniert ebenfalls nicht, weil sein Dezimalwert nahe bei 5/7 (0,714285…) liegt, so dass es auch mit 7 Armen endet. |
Wie funktioniert also der Goldene Schnitt?
| Eine der besonderen Eigenschaften des Goldenen Schnitts ist, dass er durch sich selbst definiert werden kann, etwa so: | |
| (In Zahlen: 1,61803… = 1 + 1/1,61803…) | |
| Das lässt sich zu diesem Bruch erweitern, der ewig weitergeht (man nennt ihn „fortgesetzter Bruch“): | |
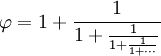 |
|
So fügt er sich geschickt zwischen einfache Brüche.
Fibonacci-Zahlen
Es gibt eine besondere Beziehung zwischen dem Goldenen Schnitt und den Fibonacci-Zahlen (0, 1, 1, 2, 3, 5, 8, 13, 21, … usw, jede Zahl ist die Summe der beiden Zahlen vor ihr).
Wenn wir zwei aufeinanderfolgende Fibonacci-Zahlen nehmen, ist ihr Verhältnis sehr nahe am Goldenen Schnitt:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

So, wie wir natürlich sieben Arme bekommen, wenn wir 0 verwenden.142857 (1/7) verwenden, erhalten wir in der Regel Fibonacci-Zahlen, wenn wir den Goldenen Schnitt verwenden.
Versuchen Sie, die Spiralarme zu zählen – die „linksdrehenden“ Spiralen, und dann die „rechtsdrehenden“ Spiralen … welche Zahlen haben Sie erhalten?
Spiralförmiges Blattwachstum

Dieses interessante Verhalten findet man nicht nur bei Sonnenblumenkernen.
Auch Blätter, Zweige und Blütenblätter können spiralförmig wachsen.
Warum? Damit neue Blätter die Sonne nicht von älteren Blättern abhalten, oder damit möglichst viel Regen oder Tau zu den Wurzeln geleitet wird.
Wenn eine Pflanze Spiralen hat, ist die Drehung in der Regel ein Bruch, der aus zwei aufeinanderfolgenden Fibonacci-Zahlen besteht, zum Beispiel:
- Eine halbe Drehung ist 1/2 (1 und 2 sind Fibonacci-Zahlen)
- 3/5 ist auch üblich (beides Fibonacci-Zahlen), und
- 5/8 auch (du hast es erraten!)
alle nähern sich immer mehr dem Goldenen Schnitt.
|
Und deshalb sind Fibonacci-Zahlen in Pflanzen sehr häufig. Hier ist ein Gänseblümchen mit 21 Blütenblättern |
 |
Aber wir sehen das nicht bei allen Pflanzen, denn die Natur hat viele verschiedene Methoden, um zu überleben.
Goldener Winkel
Bis jetzt haben wir über „Drehungen“ (volle Umdrehungen) gesprochen.
Das Äquivalent von 0,61803… Umdrehungen ist 222,4922… Grad, oder ungefähr 222,5°.
In der anderen Richtung sind es etwa 137,5°, genannt der „Goldene Winkel“.
So, wenn du das nächste Mal im Garten spazieren gehst, halte Ausschau nach dem Goldenen Winkel,
und zähle Blütenblätter und Blätter, um Fibonacci-Zahlen zu finden,
und entdecke, wie schlau die Pflanzen sind … !
Übung
Warum gehst du nicht gleich in den Garten oder Park und fängst an, Blätter und Blütenblätter zu zählen und Drehungen zu messen, um zu sehen, was du findest.
Du kannst deine Ergebnisse in dieses Formular eintragen:
| Pflanzenname oder Beschreibung: | ||
| Wachsen die Blätter in Spiralen? J / N | ||
| Zähle eine Gruppe von Blättern: | ||
| Wie viele Blätter (a)? | ||
| Wie viele volle Umdrehungen (b) ? | ||
| Drehung pro Blatt (b/a) : | ||
| Drehwinkel (360 × b/a) : | ||
| Sind Blumen vorhanden? J / N | ||
| Wie viele Blütenblätter hat Blüte 1: | ||
| Blüte 2: | ||
| Blüte 3: | ||
(Aber denk daran, die Natur hat ihre eigenen Regeln, und sie muss nicht mathematischen Mustern folgen,
aber wenn sie es tut, ist es fantastisch zu sehen.)
* Anmerkungen zur Animation
Die Samen der Sonnenblume wachsen von der Mitte nach außen, aber bei der Animation fand ich es einfacher, zuerst die jüngeren Samen zu zeichnen und dann die älteren hinzuzufügen.
Die Animation sollte länger werden, damit sie der Sonnenblume entspricht – das würde 55 Spiralen im Uhrzeigersinn und 34 Spiralen gegen den Uhrzeigersinn ergeben (aufeinander folgende Fibonacci-Zahlen). Ich wollte nur nicht, dass es zu lange dauert.
Die Spiralen sind nicht einprogrammiert – sie entstehen auf natürliche Weise, wenn man versucht, die Samen so nah wie möglich aneinander zu platzieren und sie dabei in der richtigen Drehung zu halten.

