Grundlæggende om kondensatorer, hvordan de fungerer og forskellige typer kondensatorer og deres anvendelser i kredsløb

Kondensatorer – ordet synes at antyde idéen om kapacitet, som ifølge ordbogen betyder “evnen til at rumme noget”. Det er præcis, hvad en kondensator gør – den holder elektrisk ladning. Men hvad gør den til en almindelig komponent i næsten alle elektroniske kredsløb? Lad os nedbryde stoffet bag kondensatorer for at forstå, hvad den gør, og hvordan man kan bruge dem i denne artikel.

Hvad er en kondensator?

En kondensator består i sin mest primitive form af to ledende plader, der er adskilt af et dielektrisk medium. Udtrykket dielektrisk er blot et fancy ord for en isolator, der kan polariseres, dvs. danne negative og positive ladninger på modsatte flader. Når der lægges en spænding på tværs af disse to plader, strømmer der strøm gennem de ledende plader. Den ene side bliver positivt ladet (mangel på elektroner), og den anden side bliver negativt ladet (overskud af elektroner). Vi kender alle det faktum, at ulige ladninger tiltrækker hinanden, så da pladerne er modsat ladede, tiltrækkes ladningerne på pladerne.

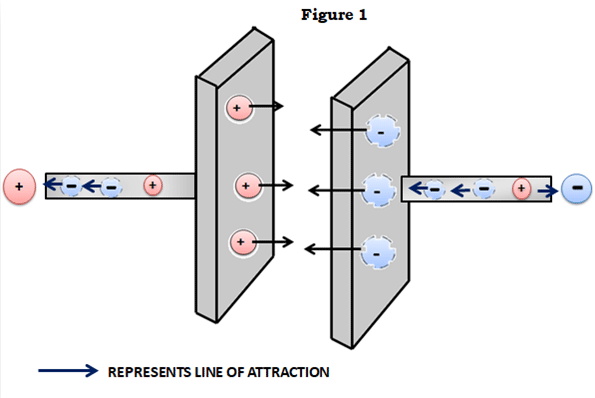
Husk, at der er en isolator mellem pladerne, så ladningerne kan ikke “flyde” for at udligne hinanden og er (ideelt set) fastlåst i en tilstand af gensidig tiltrækning og bliver siddende. Og det er sådan, kondensatorer udfører deres mest grundlæggende funktion – fastholdelse eller lagring af ladning.

Kondensatorers symbol

Da kondensatorer har to parallelle metalplader som omtalt ovenfor, repræsenterer deres symbol på en måde det samme. Det er i hvert fald let at tegne

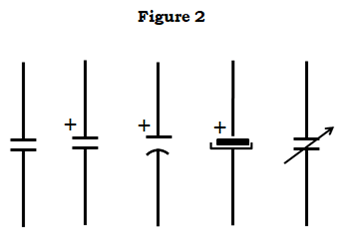
I et praktisk tilfælde er kondensatorer ikke længere blot to plader med et mellemrum mellem dem, i tilfælde af aluminiumelektrolytter har de to plader form af metalfolie rullet sammen med en afstandsstykke mellem dem i et rør.

Det andet sæt symboler står for polariserede kondensatorer, dvs. dem, der har definerede positive og negative terminaler ved intern konstruktion. Hvis man ved et uheld vender disse terminaler om, vil det næsten helt sikkert resultere i et spektakulært svigt (især for større eksemplarer), hvor der bliver kastet stykker af folie og papirmeter ud fra svigtstedet og for det meste lugter meget dårligt.

Kapacitans og spændingsværdi for en kondensator

Kondensatorer måles i farads; det er opkaldt efter den berømte britiske elektrokemiker, Michael Faraday. Enheden for kapacitans, der står for Coulomb per Volt. Coulomb (udtales “koo-lom”) er S.I.-enheden for ladning, og en volt er som bekendt enheden for spænding eller potentialforskel. Det betyder, at farad er den mængde ladning, der er lagret pr. volt potentialforskel. Denne enkle måde at betragte en kondensator matematisk på giver mulighed for en lang række fortolkninger, der kommer til udtryk i en masse dødbringende komplekse matematiske ligninger som integraler, eksponenter og vektorer, som vi ingeniører bruger, når vi arbejder med kondensatorer, men som ligger langt uden for rammerne af denne artikel. Vi vil dog komme ind på lidt interessant matematik, der vil hjælpe os med at designe kredsløb med kondensatorer senere i artiklen

Formodellen Farad (en Coulomb pr. Volt) er naturligvis en meget stor enhed til de fleste praktiske formål (da Coulomb i sig selv er en ret stor ladningsmængde, som du måske allerede ved), så de fleste kondensatorer (undtagen meget store kondensatorer) måles i mikrofarad, eller en milliondel (0,000001) af en Farad. Lad os antage, at du har en kondensator, hvor der står 25V 10uF (præfikset “u” står for mikro, det er en forvanskning af det græske symbol µ (“mu”), der betyder “mikro”) på det ydre plastikdæksel. Da hætten (i den elektroniske verden en forkortelse for kondensatorer) er normeret til 10uF, kan den holde en ladning på ti mikrocoulomb (dvs. ti milliontedele af en coulomb, 0,000010 C) pr. volt spænding over sine terminaler. Det betyder, at kondensatoren ved den maksimale spænding på 25 V kan indeholde en ladning på 25 V x 10uF, hvilket svarer til 0,000250 Coulombs.

Husk, at jeg sagde “maksimal” spænding. Maksimal spænding er nok den vigtigste værdi på kondensatoren. Den fortæller dig, hvor meget spænding en kondensator kan klare over sine terminaler, før den går KABOOM………!

Kondensatorens funktion

Helt grundlæggende er det, der sker inde i en kondensator, at isolatoren mellem pladerne gennemgår en proces, der kaldes ‘dielektrisk nedbrydning’, hvilket betyder, at isolatoren ikke længere kan isolere, da spændingen over isolatoren er for høj til, at den kan forblive en isolator. Den underliggende fysik er lidt uden for rækkevidde, men alt hvad man behøver at vide for at forstå, hvorfor dette sker, er, at ingen isolator er perfekt, dvs. op til et vist punkt. Selv den stærkeste bro kollapser, hvis den bliver overbelastet. Det samme sker her. For at reducere nedbruddet kan man øge afstanden mellem de to plader, men det kommer med en modydelse – reduceret kapacitans, da pladerne er længere fra hinanden, og ladningerne tiltrækkes ikke så meget, som de gør, når de er tættere på hinanden – ligesom den måde magneter opfører sig på.

En god tommelfingerregel ville være at bruge caps, der er normeret til en 50% højere spænding end den, som dit kredsløb kan forventes at se. Dette efterlader en stor sikkerhedsmargin. Hvis du f.eks. har brug for en cap til at afkoble (bare rolig, afkobling forklares senere i artiklen) en 12V strømforsyningsskinne, kan du slippe af sted med at bruge en 16V kondensator, men det anbefales at bruge en 25V kondensator, da det giver dig en bred sikkerhedsmargin. Okay du fandt ud af det!!! Ja 25V er selvfølgelig ikke 25% større end 12V, men 18V er ikke en standard kondensatorværdi – du vil ikke finde nogen med den spændingsværdi. Den nærmeste er 25V.

Differente typer kondensatorer

Grunden til nedbrydningsspændingsintervallerne skyldes det materiale, der anvendes som dielektrikum, hvilket også er det grundlag, som kondensatorer klassificeres på:

Aluminium elektrolytkondensatorer

Dette er nok de mest genkendelige kondensatortyper. De leveres i karakteristiske metaldåser med en plastikkappe, med klart angivne spændings- og kapacitansværdier og et hvidt bånd til angivelse af katoden. Navnet kommer af, at “pladerne”, som nævnt ovenfor, er fremstillet af kemisk ætset aluminiumsfolie. Ætsningsprocessen gør aluminiumet porøst (ligesom en svamp) og øger dets overfladeareal betydeligt, hvilket øger kapacitansen. Det dielektriske materiale er et tyndt lag af aluminiumoxid. Disse kondensatorer er fyldt med olie, der fungerer som en elektrolyt, deraf navnet. Elektrolytiske kondensatorer er polariserede på grund af deres interne konstruktion. De har stor kapacitet sammenlignet med andre medlemmer af kondensatorfamilien, men meget lavere spændinger. Du kan forvente at se elektrolytter mellem 0,1uF til monstre som 100mF og med nominelle spændinger fra et par volt til omkring 500V. Deres indre modstande har dog tendens til at være høje.

SIDEBEMÆRK: Den indre modstand i kondensatorer skyldes de materialer, som hætten er fremstillet af – f.eks. modstanden i aluminiumsfolien eller modstanden i ledningerne.

Keramiske kondensatorer

Dette er hætter med et keramisk dielektrikum. Da nedbrydningsgrænsen for det keramiske dielektrikum er ret høj, kan du forvente at se keramiske kapsler med vanvittige nedbrydningsspændinger som f.eks. 10 kV. Kapacitansen har dog tendens til at være lav, i området fra picofarads (0,0000000000000001F) til et par tiendedele mikrofarads. De er generelt meget mindre end andre typer kondensatorer, som vist på billedet. De har også meget små indre modstande.

Identificering af keramiske kondensatorer

Værdien af en keramisk kapacitet vil ikke være direkte nævnt på den keramiske kondensator. Der vil altid være et trecifret tal efterfulgt af en variabel; lad os lære, hvordan vi kan identificere værdien ved hjælp af disse tal. Overvej følgende kondensator:

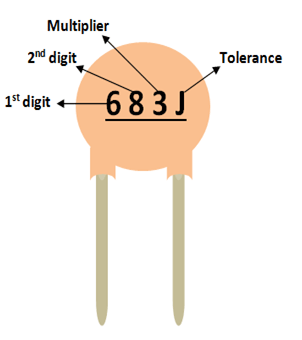
Som du kan bemærke, er disse tre cifre opdelt i to cifre, og det tredje er multiplikatoren. I dette tilfælde er 68 cifferet og 3 er multiplikatoren. Så 68 skal ganges med 10^3. Enkelt sagt er det 68 efterfulgt af 3 nuller. Derfor vil værdien af denne kondensator være 68000 pF. Bemærk, at enheden altid skal være pF. På samme måde betyder en kondensator med koden 220, at den er 22 Pico farad, da 10^0 er 0.

Spændingsværdien for kondensatoren kan findes ved hjælp af linjen under denne kode. Hvis der er en linje, er spændingsværdien 50/100V, hvis der ikke er nogen linje, er den 500V.

De mest almindeligt anvendte kondensatorværdier sammen med deres omregning i Pico Farad, Nano Farad og mikrofarad er angivet nedenfor.

Filmkondensatorer

Som navnet antyder, er dielektrikummet i disse kondensatorer en plastfilm, ofte velkendte plastmaterialer som mylar og polyester. De har de samme egenskaber som keramiske kapsler, nemlig høje nedbrydningsspændinger (på grund af plastpolymerernes opførsel) og lave kapacitanser. Den eneste forskel er, at de har tendens til at være lidt større, selv om de overfladisk set ligner keramiske kapsler. Den indre modstand er sammenlignelig med keramiske kapsler.

Tantal- og niobiumkondensatorer

Disse kapsler hører teknisk set under den elektrolytiske kategori af kondensatorer. Her er elektrolytten et fast materiale fremstillet af tantal- eller niobiumoxider. De har en meget lav indre modstand for en given kapacitans, men de er mindre immune over for overspænding sammenlignet med andre typer (keramik har det bedst) og har en tendens til at gå kaput uden større varsel og med en masse grim sort røg.

Specialkondensatorer til særlige formål

Disse omfatter sølv – glimmerkapsler, X- og Y-klassificerede kapsler osv. X- og Y-klassificerede kondensatorer er f.eks. bygget til netfiltrering – mere robust konstruktion og højere spændingsværdier, også lave kapacitanser, for at reducere den strøm, der passerer gennem den, hvis der anvendes vekselspænding, og for at begrænse den energi, der er lagret i hætten, hvis der anvendes jævnspænding.

Superkondensatorer og ultrakondensatorer

De tager kondensatorer til et helt nyt niveau med stærkt forøgede kapacitanser, nogle gange i størrelsesordenen hundreder af Farad! Dette er muligt på grund af noget smart kemi. Superkondensatorer og ultrakondensatorer slår bro over kløften mellem kondensatorer og kemiske batterier. De findes dog i meget lave spændinger.

Og det er stort set alle de almindelige typer kondensatorer, som man almindeligvis kan støde på i elektronikkens verden.

Hvordan kondensatorer opfører sig i kredsløb

En nyttig første opgave vil være at lære at beregne energilagrene i en kondensator, som er givet ved formlen,

E = 1/2CV2

Hvor E er den lagrede energi i joule, C er kapacitansen i farads og V er spændingen i volt. Bemærk, at denne ligning har samme form som mange andre newtonske ligninger for energi, et pænt påskeæg!

Sæt, at du har en cap, der er normeret til en spænding på 50V og med en kapacitans på 1000uF, vil den lagrede energi ved de fulde 50V være:

1/2 * 0.001000F * 50V * 50V

Hvilket svarer til en sølle 1,25J lagret energi.

Dette afslører en stor ulempe ved kondensatorer som energilagringsenheder – den lagrede energi for en given størrelse er meget lav, et batteri af samme størrelse ville have mindst tusind gange mere lagret energi! Kapsler har imidlertid meget lavere indre modstande end kemiske batterier, hvilket gør det muligt for dem at aflade al deres lagrede energi hurtigt. Hvis man kortslutter et batteri, vil det kun blive varmt på grund af den energi, der går tabt på grund af den interne modstand, men hvis man kortslutter en kondensator, vil der kun opstå nogle få gnister, da al ladningen afgives på én gang, uden at kondensatoren tager skade.

For det andet er der en anden fin formel, der relaterer spænding, strøm og kapacitans:

I/C = dV/dt

Hvor I er den strøm, der tilføres kondensatoren i ampere, C er kapacitansen i farads og dV/dt er ændringshastigheden af spændingen over kondensatorterminalerne. Tænk på dette i form af dets enhed – volt pr. sekund for en given strøm og kapacitans. Du skal ikke bekymre dig om det lille “d”, det er bare en matematisk måde at sige “til grænsen nul”.

Lad os sige, at du har en strømforsyning, der spytter en konstant spænding på 5V ud ved en konstant strøm på 1mA, så kan vi ved at omarrangere ligningen finde den tid, det tager at oplade en 100uF kondensator til 5V:

dt = CdV/I

dt = (0.000100F * 5V)/0,001A

dt = 0,5 sekunder

Sådan vil kondensatoren blive opladet til 5V på 0,5 sekunder. (Husk, at en kondensator kun kan oplade op til den maksimale spænding, der tilføres den, aldrig mere, de kan ikke på magisk vis “skabe” spænding.)

Denne forudsigelige opførsel af en kondensator gør den meget anvendelig til at generere tidsforsinkelser, f.eks. med lidt ekstra kredsløb. Du kan omarrangere ligningen for at opnå tid.

Nu kommer vi til de gode ting – egentlige kondensatorkredsløb!

Kondensatorers adfærd i kredsløb

Lad os begynde enkelt – de forskellige måder, hvorpå kondensatorer kan forbindes sammen. Det er stort set det samme som at forbinde to modstande – du kan enten forbinde dem i serie eller parallelt.

Kondensatorer i parallel

Figuren nedenfor viser tre kondensatorer, der er forbundet parallelt, med alle de respektive positive og negative terminaler forbundet sammen (under forudsætning af, at kapslerne er polariserede). Den samlede kapacitans i denne opstilling er simpelthen summen af alle kapacitanserne for alle kondensatorer i kredsløbet. Dette giver mening, da en parallelforbindelse af kondensatorpladerne øger overfladen, hvilket øger kapacitansen.

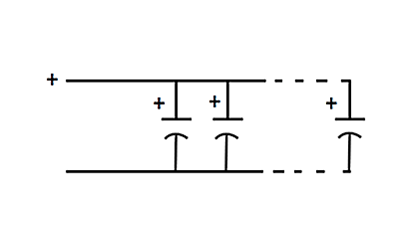
Den maksimale spænding, som denne form for arrangement kan håndtere, er spændingen for den mindste kondensator, da i spændingen er fælles for alle kapslerne.

Et eksempel skulle kunne tydeliggøre dette. Lad os antage, at du har to kondensatorer, den ene med værdierne 25V 470uF og den anden 35V 1000uF. Den samlede kapacitans ville være 470uf + 1000uF = 1470uF. Den maksimale spænding, som du kan lægge over denne kondensatorbank (en række kondensatorer, der er forbundet med hinanden, kan kaldes en kondensator “bank”), vil imidlertid kun være 25 V. Hvis du sætter noget højere end det over denne bank, vil der flyve gnister, da du overskrider den maksimale spænding for kondensatoren på 25V.

Kondensatorer i serie

Sammenkobling af kondensatorer i parallel er især nyttig, når du ønsker en stor kapacitet, og du kun har små værdier. Ved at sætte de mindre værdier af kapsler sammen parallelt får du i sidste ende den større værdi og klarer opgaven, forudsat at du er opmærksom på spændingen.

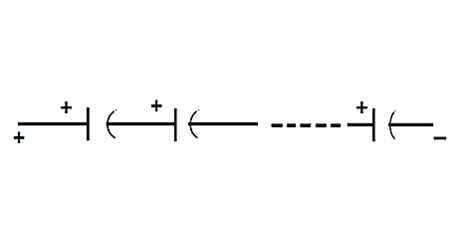
Nu er det lidt mere kompliceret at sætte kondensatorer i serie. Kapacitansen er givet ved formlen:

1/Ctotal = 1/C1 + 1/C2 + … + 1/Cn

Hvor C1, C2…Cn er kapacitanserne for hver enkelt kondensator, der anvendes i kredsløbet.

Den spænding, som banken nu kan håndtere, er summen af alle de nominelle spændinger.

Hvis du får en kondensator, der er normeret til 10V 1uF, og en kondensator, der er normeret til 50V 10uF, så er den spænding, som banken kan klare i serie, 10V + 50V = 60V. Kapacitansen giver 0,9091uF.

Kondensatorspænding vs. tid

Hvad sker der, hvis vi ønsker at oplade en kondensator? Vi kan bare forbinde den over en spændingskilde, som i figuren nedenfor. Det, der ville ske her, er, at i det øjeblik spændingskilden tilsluttes, forudsat at kondensatoren er helt afladet, vil ladningerne skynde sig at ophobe sig på pladerne, hvilket fører til en meget stor (i teorien uendelig!) strømspids, der kun er begrænset af kondensatorens indre modstand. Dette er naturligvis ikke ønskeligt, hvis din strømforsyning tilfældigvis er noget som et batteri. En fornuftig idé ville være at tilføje en modstand i serie med kondensatoren og spændingskilden for at begrænse strømmen som i figuren, og voila! Du har noget, som ingeniører kalder et RC-kredsløb, “R” for modstand og “C” for kondensator!

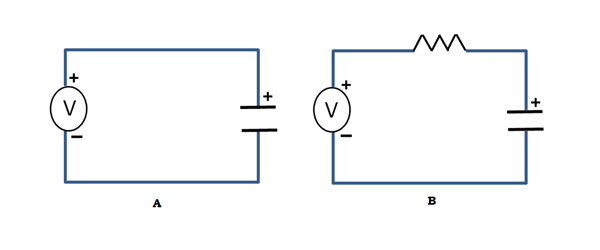
Dette kredsløb viser en interessant opførsel. Når spændingen er tilsluttet den side af modstanden, der er markeret med ‘I’, stiger spændingen på kondensatoren langsomt, da strømmen er begrænset. Grafen ser nogenlunde sådan ud:

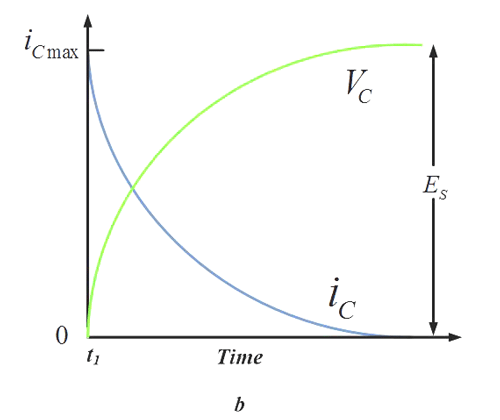
De mere matematisk indstillede af mine seere vil genkende formen på hældningen – den ligner den eksponentielle funktions form!

Huskede du, at jeg sagde, at kapsler kunne bruges til at generere tidsforsinkelser? Dette er en måde at gøre det på uden en konstant strømkilde (som kræver nogle ekstra kredsløb). Da den tid, det tager at nå en bestemt spænding, kan forudsiges, hvis vi kender kapacitansen, spændingen og modstanden, kan vi skabe tidsforsinkede kredsløb.

Produktet af modstand og kapacitans, RC, er kendt som kredsløbets tidskonstant. Denne parameter bliver nyttig til rent faktisk at bestemme tiden til at nå en given spænding nøjagtigt, som det fremgår af nedenstående graffigur.

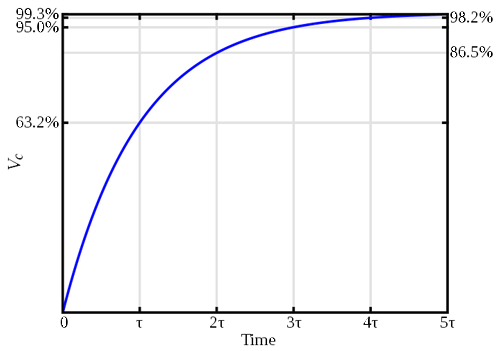
Fra grafen kan man se, at kondensatoren når 63% af den påførte spænding på én tidskonstant osv.

Dette er det princip, som den helårs 555-timer anvender, selv om designligningerne er lidt anderledes.

En anden interessant anvendelse af RC-kredsløb er signalfiltrering, dvs. fjernelse af et elektrisk signal med en uønsket frekvens fra et kredsløb. RC-kredsløbet tager en given tid til at oplade og aflade fra en kilde. Hvis vi anvender en periodisk bølge med en tidsperiode, der er større end RC, vil det samme signal fremkomme på udgangen med meget lille forvrængning. Men når frekvensen øges, ændrer signalet polaritet hurtigere, end kredsløbet kan oplade og aflade, og efter et vist punkt forsvinder signalet, og det eneste, man står tilbage med, er ren jævnstrøm! Dette kaldes signaldæmpning. Som du kan se, fungerer et RC-kredsløb som et filter, der blokerer vekselstrømssignaler (selv dem, der overlejres af jævnstrøm, dvs. har en jævnstrømsforskydning) over en vis frekvens. Denne type filter kaldes et lavpasfilter, det vil sige, at det lader lave frekvenser passere, men ikke høje frekvenser.

Kondensatorer i vekselstrømskredsløb

Kondensatorer opfører sig på en interessant måde, når de er placeret i vekselstrømskredsløb. De kan opfattes som frekvensafhængige modstande, set fra signalets synsvinkel. Som det fremgår ovenfor, blokerer RC-kredsløbet al vekselstrøm fra et signal, men hvad sker der, når en kondensator er forbundet i serie med en vekselspændingskilde? Det stik modsatte!

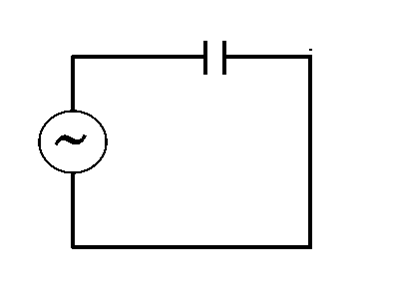
Da kondensatoren blot er to metalplader adskilt af en isolator, lader den ikke nogen jævnstrøm passere igennem sig. Et vekselstrømssignal har imidlertid konstant skiftende spændinger, så den ene plade ser en skiftende spænding og inducerer den modsatte ladning på den anden plade, som vist i figuren:

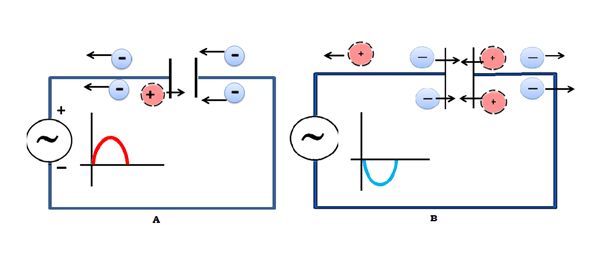
Dette har den overordnede virkning, at det lader strøm “passere” gennem kondensatoren ved relativt høje frekvenser. Tilføjelsen af en modstand parallelt med udgangen giver et højpasfilter, dvs. et filter, der kun lader strømmen passere ved høje frekvenser og blokerer alle jævnstrømssignaler.

En kondensators “vekselstrømsmodstand” eller impedans er givet ved formlen:

XC = 1/(2*π*f*C)

Hvor XC er den kapacitive reaktans eller impedans, f er frekvensen og C er kapacitansen. Du kan bruge denne formel til at beregne den virtuelle “modstand”, som en kondensator har i et vekselstrømskredsløb.

Hvor kondensatorer findes i naturen

Okay, det var nok teori. Lad os se på de mange anvendelsesmuligheder for kondensatorer.

Det første sted, man kan forvente at se kondensatorer, er i strømforsyninger af alle slags som filtre og til afkobling. De fungerer som ladningsreservoirer – de leverer hurtig strøm, når belastningen har brug for det.

Her er to oscilloskopoptagelser, der viser effekten af at have og ikke at have en kondensator på tværs af ledningerne i en strømforsyning. Som du kan se, reducerer det at have kondensatorer dramatisk “støjen” på strømforsyningsskinnerne og beskytter dermed sarte dele mod pludselige spændingsspidser.

De kaldes også “afkoblingskondensatorer”, da de “afkobler” dele af det kredsløb, over hvilke de er monteret, fra strømforsyningen. Nogle gange kan strømledningerne på et kredsløbskort være ret lange og have en høj induktans og modstand. Dette kan føre til, at de leverer mindre strøm end normalt. At have en kondensator i enden af forsyningsledningen er som at have et mindre midlertidigt “batteri” over enheden, der leverer strømstød, når der er behov for det, og som oplades, når enheden bruger lidt strøm.

Du kan bruge formlen I/C = dV/dt til at beregne den nødvendige kapacitet til at fjerne “ripple”-spænding fra strømforsyningens terminaler.

Sæt, at du har en strømforsyning, hvis spænding varierer fra 11,5 V til 12 V (ripple) hver 10 ms, hvilket er almindeligt i netdrevne enheder på grund af frekvensen på 50 Hz, og du skal placere en cap over terminalerne for at udjævne spændingen. Hvis belastningsstrømmen i dette tilfælde er 1A, kan vi omarrangere formlen på denne måde for at finde ud af kapaciteten:

(I * dt)/dV

Hvor I er belastningsstrømmen, dt er støjens tidsperiode, og dV er ripplespændingen. Ved at substituere værdierne finder vi, at vi har brug for en kapacitet på 20000uF. Nu kan det virke som meget, men du kan slippe af sted med meget mindre. Den opnåede værdi tjener kun som en retningslinje.

I det virkelige liv kan du finde flere typer og værdier af kondensatorer på tværs af strømledninger, dette er for at reducere støjindholdet på tværs af mange frekvenser og få den mest jævne spænding muligt.

En anden anvendelse af kondensatorer er i komplicerede filtre som dette:

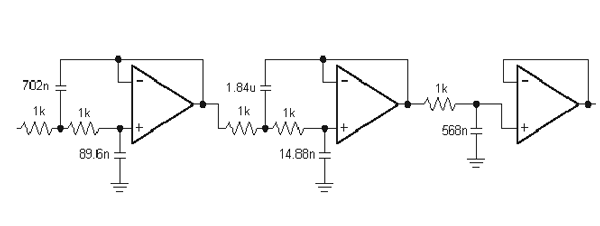
Men et mere simpelt filter ville være RC-filteret, et interessant filter er beskrevet her.

Alle kender Arduino-mikrocontrollerboardet. Et alsidigt værktøj, men har du aldrig undret dig over, hvorfor de analoge udgange spytter et digitalt PWM-signal ud? Det skyldes, at de er designet til at blive brugt med et eksternt filtreringsnetværk til at udjævne PWM-spændingen til en ægte analog spænding. Dette kan gøres med dele så enkle som en 1K-modstand og en 10uF-kondensator. Prøv det!

En anden anvendelse, som nævnt ovenfor, er timing. En simpel oscillator kan bygges ved hjælp af en NAND-gate (prøv at finde ud af, hvorfor AND-gates ikke virker), en modstand og en kondensator.

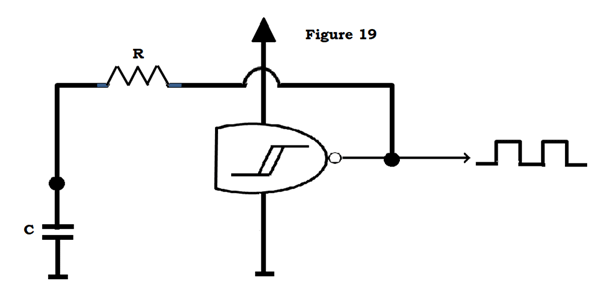
Antaget, at der i begyndelsen ikke er nogen spænding over kondensatoren, ser NAND-indgangene (som er bundet sammen) tæt på 0V over dem og tænder udgangen. Kapslen oplades nu gennem modstanden. Når den når gateens “high”-tærskel, slår outputtet lavt, og cap’en aflader nu. Denne cyklus fortsætter for at producere en firkantet udgangsbølge med en frekvens, der afhænger af værdierne af R og C.

Endeligt er en anden interessant anvendelse af kondensatorer energilagring. Selvfølgelig kan kondensatorer ikke måle sig med batterier, men til nogle anvendelser, der har brug for energien hurtigt, er caps de bedste til opgaven.

Enheder som coilguns (mere kan findes på nettet) har brug for en stor strømimpuls for at accelerere projektilet, så højspændingskondensatorer anvendes til formål som dette, ofte med værdier som 450V 1500uF, som kan lagre betydelige mængder energi.