
Kasvit voivat kasvattaa uusia soluja spiraalimaisesti, kuten tämän kauniin auringonkukan siemenkuvio.
Spiraali syntyy luonnollisesti, koska jokainen uusi solu muodostuu kierroksen jälkeen.
”Uusi solu, sitten kierros,
silloin toinen solu, sitten kierros, …”
Miten pitkälle käännytään?
Jos olisit kasvi, kuinka paljon voisit kääntyä uusien solujen välillä?
Jos et käänny lainkaan, saat suoran linjan.
![]()
Mutta se on hyvin huono suunnittelu ….haluat jotain pyöreää, joka pysyy kasassa ilman aukkoja.
Miksi et yritä löytää itsellesi parasta arvoa?
Kokeile eri arvoja, kuten 0,75, 0,9, 3,1416, 0,62 jne.
Muista, että yrität tehdä kuvion, jossa ei ole aukkoja alusta loppuun:
(Muuten, ei ole väliä kokonaisen numeron osalla, kuten 1. tai 5., koska ne ovat täysiä kierroksia, jotka osoittavat meitä takaisin samaan suuntaan.)
Mitä sait?
Jos sait jotain, joka päättyy kuten 0,618 (tai 0,382, joka on 1 – 0,618), niin ”Onneksi olkoon, olet onnistunut kasvikunnan jäsen!”
 |
Tämä johtuu siitä, että kultainen leikkaus (1.61803…) on paras ratkaisu, ja auringonkukka on löytänyt tämän omalla luonnollisella tavallaan. Kokeile … sen pitäisi näyttää tältä. |
Miksi?
Jokainen luku, joka on yksinkertainen murtoluku (esimerkki: 0.75 on 3/4, ja 0,95 on 19/20 jne.) muodostaa jonkin ajan kuluttua kuvion, jossa viivat pinoutuvat päällekkäin, jolloin syntyy aukkoja.
Mutta kultainen leikkaus (sen symboli on kreikkalainen kirjain Phi, kuvassa vasemmalla) on asiantuntija siinä, että se ei ole mikään murtoluku.
Se on irrationaaliluku (mikä tarkoittaa, ettemme voi kirjoittaa sitä yksinkertaisena murtolukuna), mutta enemmänkin … se on niin kaukana siitä, että se olisi lähelläkään mitään murtolukua.
| Oleminen pelkästään irrationaalinen ei riitä | |
|---|---|
 |
Pi (3.141592654…), joka on myös irrationaalinen. Epäonnekseen sen desimaaliluku on hyvin lähellä 1/7 (= 0.142857…), joten se päätyy 7 käsivarteen. |
 |
e (2.71828….), joka on myös irrationaalinen, ei myöskään toimi, koska sen desimaaliluku on lähellä 5/7 (0.714285…), joten sekin päätyy 7 varteen. |
Miten siis kultainen leikkaus toimii?
| Yksi kultaisen leikkauksen erikoisominaisuuksista on se, että se voidaan määritellä itsensä suhteen, esimerkiksi näin: | |
| (Luvuilla: 1.61803… = 1 + 1/1.61803….) | |
| Tämä voidaan laajentaa tällaiseksi murtoluvuksi, joka jatkuu ikuisesti (jota kutsutaan ”jatkuvaksi murtoluvuksi”): | |
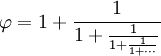 |
|
Se liukuu siis kätevästi yksinkertaisten murtolukujen joukkoon.
Fibonaccin luvut
Kultaisen leikkauksen ja Fibonaccin lukujen välillä on erityinen suhde (0, 1, 1, 1, 2, 3, 5, 8, 13, 21, … jne, jokainen luku on kahden sitä edeltävän luvun summa).
Kun otamme kaksi peräkkäistä (peräkkäistä) Fibonaccin lukua, niiden suhde on hyvin lähellä kultaista leikkausta:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Aivan kuten luonnollisesti saamme seitsemän käsivartta kun käytämme 0.142857 (1/7), meillä on taipumus saada Fibonaccin lukuja, kun käytämme kultaista leikkausta.
Kokeile laskea spiraalivarsia – ”vasemmalle kääntyviä” spiraaleja ja sitten ”oikealle kääntyviä” spiraaleja … mitä lukuja sait?
Spiraalinen lehtien kasvu

Tämä mielenkiintoinen käyttäytyminen ei esiinny vain auringonkukan siemenissä.
Lehdet, oksat ja terälehdet voivat myös kasvaa spiraalimaisesti.
Miksi? Jotta uudet lehdet eivät estäisi aurinkoa vanhemmilta lehdiltä, tai jotta mahdollisimman suuri määrä sadetta tai kastetta ohjautuisi juurille.
Tosiasiassa, kun kasvilla on spiraaleja, kierto on yleensä murtoluku, joka on tehty kahdella peräkkäisellä (peräkkäisellä) Fibonaccin luvulla, esimerkiksi:
- Puolikierto on 1/2 (1 ja 2 ovat Fibonaccin lukuja)
- 3/5 on myös yleinen (molemmat Fibonaccin lukuja), ja
- 5/8 on myöskin (arvasitko!)
kaikki yhä lähempänä kultaista leikkausta.
|
Ja siksi Fibonacciluvut ovat hyvin yleisiä kasveissa. Tässä on päivänkakkara, jolla on 21 terälehteä |
 |
Mutta emme näe tätä kaikissa kasveissa, koska luonnossa on monia erilaisia selviytymiskeinoja.
Kultainen kulma
Tähän asti olemme puhuneet ”kierroksista” (täysistä kierroksista).
0,61803… kierrosta vastaa 222,4922… astetta eli noin 222,5°.
Toisessa suunnassa se on noin 137,5°, jota kutsutaan ”kultaiseksi kulmaksi”.
Kun siis seuraavan kerran kävelet puutarhassa, etsi kultainen kulma,
ja laske terälehdet ja lehdet löytääksesi Fibonacci-lukuja,
ja huomaa, kuinka nokkelia kasvit ovat … !
Harjoitus
Mene nyt heti puutarhaan tai puistoon ja ala laskea lehtiä ja terälehtiä ja mittaa kierroksia ja katso, mitä löydät.
Voit kirjoittaa tuloksesi tähän lomakkeeseen:
| Kasvin nimi tai kuvaus: | |||
| Kasvavatko lehdet spiraalissa? Y / N | |||
| Laskekaa ryhmä lehtiä: | |||
| Montako lehteä (a) ? | |||
| Montako täyttä kierrosta (b) ? | |||
| Kierros per lehti (b/a) : | |||
| Kierron kulma (360 × b/a) : | |||
| Onko kukkia? Y / N | |||
| Montako terälehteä kukassa 1: | |||
| Kukka 2: | |||
| Kukka 3: | |||
(Mutta muistakaa, että luonnolla on omat sääntönsä, eikä sen tarvitse noudattaa matemaattisia kaavoja,
mutta kun se tekee niin, se on mahtavaa nähdä.)
* Huomioita animaatiosta
Auringonkukan siemenet kasvavat keskeltä ulospäin, mutta animaatiossa koin helpommaksi piirtää ensin nuoremmat siemenet ja lisätä sitten vanhemmat.
Animaation pitäisi jatkua pidempään, jotta se olisi samansuuruinen kuin auringonkukka – näin saataisiin aikaan 55 myötäpäivään menevää kierrettä ja 34 vastapäivään menevää kierrettä (peräkkäisiä Fibonaccin numeroita). En vain halunnut, että se kestäisi liian kauan.
Spiraaleja ei ole ohjelmoitu siihen – ne syntyvät luonnollisesti, kun siemenet yritetään sijoittaa mahdollisimman lähelle toisiaan pitäen ne samalla oikeassa kierrossa.

