
Las plantas pueden crecer nuevas células en espiral, como el patrón de semillas de este hermoso girasol.
La espiral se produce de forma natural porque cada nueva célula se forma después de un giro.
«Nueva célula, luego giro,
luego otra célula, luego giro, …»
¿Cuánto hay que girar?
Así que, si fueras una planta, ¿cuánto giro tendrías entre las nuevas células?
Si no giras en absoluto, obtienes una línea recta.
![]()
Pero eso es un diseño muy pobre … quieres algo redondo que se mantenga unido sin huecos.
¿Por qué no intentas encontrar el mejor valor para ti?
Prueba diferentes valores, como 0,75, 0,9, 3,1416, 0,62, etc.
Recuerda que estás intentando hacer un patrón sin huecos desde el principio hasta el final:
(Por cierto, no importa la parte de los números enteros, como el 1. o el 5. porque son revoluciones completas que nos apuntan en la misma dirección.)
¿Qué obtuviste?
Si obtuviste algo que termina como 0,618 (o 0,382, que es 1 – 0,618) entonces «¡Felicitaciones, eres un miembro exitoso del reino vegetal!»
 |
Eso se debe a que la Razón Áurea (1.61803…) es la mejor solución, y el Girasol lo ha descubierto de forma natural. Prueba… debe quedar así. |
¿Por qué?
Cualquier número que sea una fracción simple (ejemplo: 0.75 es 3/4, y 0,95 es 19/20, etc) hará, al cabo de un tiempo, un patrón de líneas que se apilan, lo que hace que haya huecos.
Pero la Proporción Áurea (su símbolo es la letra griega Phi, mostrada a la izquierda) es una experta en no ser ninguna fracción.
Es un Número Irracional (lo que significa que no podemos escribirlo como una simple fracción), pero más que eso… es lo más lejos que podemos estar de ser cualquier fracción.
| No basta con ser irracional | |
|---|---|
 |
Pi (3,141592654…), que también es irracional. Desgraciadamente tiene un decimal muy cercano a 1/7 (= 0,142857…), por lo que acaba con 7 brazos. |
 |
e (2,71828…) también irracional, tampoco funciona porque su decimal es cercano a 5/7 (0,714285…), por lo que también acaba con 7 brazos. |
Entonces, ¿cómo funciona la razón áurea?
| Una de las propiedades especiales de la Proporción Áurea es que se puede definir en términos de sí misma, así: | |
| (En números: 1,61803… = 1 + 1/1,61803…) | |
| Eso puede expandirse en esta fracción que se prolonga para siempre (llamada «fracción continua»): | |
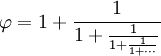 |
|
Así, se cuela limpiamente entre las fracciones simples.
Números de Fibonacci
Hay una relación especial entre la Proporción Áurea y los Números de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21, … etc, cada número es la suma de los dos anteriores).
Cuando tomamos dos Números de Fibonacci sucesivos (uno tras otro), su relación es muy cercana a la Razón Áurea:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
||
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Así, al igual que obtenemos naturalmente siete brazos cuando utilizamos 0.142857 (1/7), tendemos a obtener Números de Fibonacci cuando utilizamos la Proporción Áurea.
Trate de contar los brazos de la espiral – las espirales que «giran a la izquierda», y luego las espirales que «giran a la derecha» … ¿qué números obtuvo?
Crecimiento de las hojas en espiral

Este interesante comportamiento no sólo se encuentra en las semillas de girasol.
Las hojas, las ramas y los pétalos también pueden crecer en espiral.
¿Por qué? Para que las hojas nuevas no bloqueen el sol de las más viejas, o para que la máxima cantidad de lluvia o rocío se dirija hacia las raíces.
De hecho, cuando una planta tiene espirales la rotación tiende a ser una fracción hecha con dos Números de Fibonacci sucesivos (uno tras otro), por ejemplo:
- Una media rotación es 1/2 (1 y 2 son Números de Fibonacci)
- 3/5 también es común (ambos Números de Fibonacci), y
- 5/8 también (¡lo has adivinado!)
todo ello acercándose cada vez más a la Proporción Áurea.
|
Y por eso los Números de Fibonacci son muy comunes en las plantas. Aquí tienes una margarita con 21 pétalos |
 |
Pero no vemos esto en todas las plantas, ya que la naturaleza tiene muchos métodos diferentes de supervivencia.
Ángulo de oro
Hasta ahora hemos estado hablando de «vueltas» (rotaciones completas).
El equivalente a 0,61803… rotaciones es 222,4922… grados, o sea unos 222,5°.
En la otra dirección son unos 137,5°, lo que se llama el «Ángulo de Oro».
Así que, la próxima vez que pasees por el jardín, busca el Ángulo de Oro,
y cuenta los pétalos y las hojas para encontrar los Números de Fibonacci,
y descubre lo inteligentes que son las plantas… !
Ejercicio
Por qué no vas al jardín o al parque ahora mismo, y empiezas a contar hojas y pétalos, y a medir rotaciones para ver qué encuentras.
Puedes escribir tus resultados en este formulario:
| Nombre de la planta o descripción: | ||
| ¿Crecen las hojas en espiral? S / N | ||
| Cuente un grupo de hojas: | ||
| ¿Cuántas hojas (a) ? | ||
| Ángulo de rotación (360 × b/a) : | ||
| ¿Hay flores? S / N | ||
| Cuántos pétalos tiene la Flor 1: | ||
(Pero recuerda, la naturaleza tiene sus propias reglas, y no tiene por qué seguir patrones matemáticos,
pero cuando lo hace es impresionante de ver.)
* Notas sobre la animación
Las semillas del girasol crecen desde el centro hacia fuera, pero en la animación me pareció más fácil dibujar primero las semillas más jóvenes y añadir las más viejas.
La animación debería continuar más tiempo para ser igual que el girasol – esto resultaría en 55 espirales en el sentido de las agujas del reloj y 34 espirales en sentido contrario (Números de Fibonacci sucesivos). Simplemente no quería que tomara demasiado tiempo.
Las espirales no están programadas en él – se producen de forma natural como resultado de tratar de colocar las semillas tan cerca como sea posible, mientras que los mantiene en la rotación correcta.

