In der untenstehenden Frequenztabelle findest du A = 440 Hz, und dann
A# = 466.16 Hz,
B = 493.88 Hz,
C = 523.25 Hz, usw.
Auch das mittlere C findest du: 261.63 Hz.
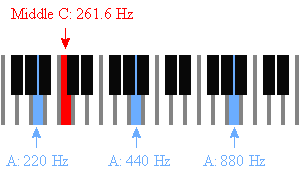
Tabelle der musikalischen Frequenzen
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
130.82
138.59
146.83
155.56
164.81
174.61
185
196
207.65
220
233.08
246.94
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Häufigkeit
261.63
277.18
293.66
311.13
329.63
349.23
369.99
392
415.3
440
466.16
493.88
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequenz
523.25
554.37
587.33
622.25
659.26
698.46
739.99
783.99
830.61
880
932.33
987.77
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
C
Frequenz
1046.5
1108.73
1174.66
1244.51
1318.51
1396.91
1479.98
1567.98
1661.22
1760
1864.66
1975.53
2093.00
Diese werden gefunden mit
Frequenz `= 440×2^(n“/“12)`
für `n = -21, -19, …, 27`
Woher stammt diese Formel?
Dieses Problem erinnerte mich an den Zinseszins, den wir früher in Money Math kennen gelernt haben. Die Frequenz muss sich alle 12 Noten verdoppeln (weil es in jeder Oktave 7 weiße und 5 schwarze Noten gibt).
Hier ist ein Diagramm dieser Beziehung:
Frequenz `= 440×2^(n“/“12)`
Dies ist eine Exponentialkurve, die wir schon in Graphen von Exponentialfunktionen kennengelernt haben.
Gleichschwebende Stimmung
Ein interessantes Problem stellt sich den Musikinstrumentenbauern schon seit Hunderten von Jahren. Um eine „perfekte Quinte“ zu erhalten (z.B. das Intervall zwischen A und dem darüber liegenden E), müssen wir eine Note spielen, die das 1,5-fache der Frequenz von A hat.
Auf einer Geige (oder Bratsche oder einem anderen bundlosen Saiteninstrument) ist dies möglich, und wir können ein schönes, perfektes E mit 440 × 1,5 = 660 Hz spielen. Aber beachten Sie (aus der obigen Frequenztabelle), dass ein Klavier, das dieselbe Note spielt, E `= 659,26\ „Hz“` spielt.
Vor etwa 400 Jahren wurden Tastaturen (normalerweise Cembalos und Orgeln) für eine bestimmte Gruppe von Tasten gestimmt, so dass alle Instrumente, insbesondere Streicher, in diesen Tasten „richtig“ klangen. Das Cembalo klang in diesen Tonarten großartig, aber ziemlich schrecklich in anderen, nicht verwandten Tonarten (z.B. B).
Es gab tatsächlich mehrere verschiedene Stimmsysteme, die zu Bachs Zeiten in Gebrauch waren, darunter die mitteltönige Stimmung (die darauf abzielte, die großen Terzen gut klingen zu lassen, sich aber nicht so sehr um die Qualität der großen Quinten kümmerte, was zur Folge hatte, dass einige Tonarten nicht verwendet werden konnten) und Werckmeisters Stimmung von 1691, die es den Komponisten erlaubte, Musik in jeder Tonart zu komponieren (was zur Folge hatte, dass die verschiedenen Tonarten eine unterschiedliche klangliche Qualität hatten).
Zu Beginn des 20. Jahrhunderts beschloss man, die Tastaturen so zu stimmen, dass die Töne gleichmäßig verteilt waren (wie die Frequenzen in der oben dargestellten Tabelle). Dies wird als gleichschwebend temperierte Stimmung bezeichnet. Eine solche Stimmung war schon zu Bachs Zeiten bekannt, wurde aber verworfen, weil sie als zu „fade“ galt (alle Tasten haben die gleiche Tonqualität) und es keine Frequenzmessgeräte gab, die eine exakte Stimmung ermöglicht hätten.
Unglücklicherweise bedeutet die gleichschwebend temperierte Stimmung, dass alle Streichinstrumente die leichten Stimmungsunterschiede zwischen den Instrumenten berücksichtigen müssen, wenn auch Tastaturen beteiligt sind. Aus diesem Grund sind Streicher in der Regel am glücklichsten, wenn sie nur mit anderen Saiten spielen.
top
Suche IntMath
Online Trigonometry Solver
Dieser Trigonometrie-Löser kann eine breite Palette von mathematischen Problemen lösen.
Go to: Online Trigonometrie-Löser