Selection Sort – Algorithmus, Quellcode, Zeitkomplexität

Dieser Artikel ist Teil der Serie „Sortieralgorithmen: Ultimativer Leitfaden“ und…

• beschreibt, wie Selection Sort funktioniert,
• beinhaltet den Java-Quellcode für Selection Sort,
• zeigt, wie man seine Zeitkomplexität ableitet (ohne komplizierte Mathematik)
• und prüft, ob die Leistung der Java-Implementierung dem erwarteten Laufzeitverhalten entspricht.

Den Quellcode für die gesamte Artikelserie finden Sie in meinem GitHub-Repository.

Beispiel: Sorting Playing Cards

Das Sortieren von Spielkarten auf die Hand ist das klassische Beispiel für Insertion Sort.

Selection Sort kann auch mit Spielkarten illustriert werden. Ich kenne niemanden, der seine Karten auf diese Weise aufhebt, aber als Beispiel funktioniert es ganz gut 😉

Zunächst legt man alle Karten offen vor sich auf den Tisch. Du suchst dir die kleinste Karte und nimmst sie auf die linke Seite deiner Hand. Dann suchst du die nächstgrößere Karte und legst sie rechts von der kleinsten Karte ab, und so weiter, bis du schließlich die größte Karte ganz rechts aufnimmst.

Unterschied zum Einlegesortieren

Beim Einlegesortieren nehmen wir die nächste unsortierte Karte und fügen sie an der richtigen Stelle in die sortierten Karten ein.

Das Auswahlsortieren funktioniert quasi andersherum: Wir wählen die kleinste Karte aus den unsortierten Karten aus und fügen sie dann – eine nach der anderen – an die bereits sortierten Karten an.

Selection Sort Algorithmus

Der Algorithmus lässt sich am einfachsten anhand eines Beispiels erklären. In den folgenden Schritten zeige ich, wie man das Feld mit Selection Sort sortiert:

Schritt 1

Wir teilen das Feld in einen linken, sortierten Teil und einen rechten, unsortierten Teil. Der sortierte Teil ist zu Beginn leer:

Schritt 2

Wir suchen nach dem kleinsten Element im rechten, unsortierten Teil. Dazu merken wir uns zunächst das erste Element, die 6. Wir gehen zum nächsten Feld, wo wir mit der 2 ein noch kleineres Element finden. Wir gehen über den Rest des Arrays und suchen nach einem noch kleineren Element. Da wir keins finden, bleiben wir bei der 2. Wir setzen sie an die richtige Stelle, indem wir sie mit dem ersten Element vertauschen. Dann verschieben wir die Grenze zwischen den Array-Abschnitten um ein Feld nach rechts:

Schritt 3

Wir suchen wieder im rechten, unsortierten Teil nach dem kleinsten Element. Diesmal ist es die 3; wir tauschen sie mit dem Element an zweiter Stelle:

Schritt 4

Wieder suchen wir im rechten Teil nach dem kleinsten Element. Es ist die 4, die sich bereits an der richtigen Stelle befindet. Wir brauchen also in diesem Schritt keine Vertauschung vorzunehmen und verschieben nur die Abschnittsgrenze:

Schritt 5

Als kleinstes Element finden wir die 6. Wir tauschen es mit dem Element am Anfang des rechten Teils, der 9:

Schritt 6

Als kleinstes der beiden verbleibenden Elemente ist die 7. Wir tauschen es mit der 9:

Algorithmus beendet

Das letzte Element ist automatisch das größte und damit an der richtigen Stelle. Der Algorithmus ist beendet, und die Elemente sind sortiert:

Selection Sort Java Source Code

In diesem Abschnitt finden Sie eine einfache Java-Implementierung von Selection Sort.

Die äußere Schleife iteriert über die zu sortierenden Elemente und endet nach dem vorletzten Element. Wenn dieses Element sortiert ist, wird das letzte Element automatisch mitsortiert. Die Schleifenvariable i zeigt immer auf das erste Element des rechten, unsortierten Teils.

In jedem Schleifenzyklus wird das erste Element des rechten Teils zunächst als das kleinste Element min angenommen; seine Position wird in minPos gespeichert.

Die innere Schleife iteriert dann vom zweiten Element des rechten Teils bis zu seinem Ende und ordnet min und minPos immer dann neu zu, wenn ein noch kleineres Element gefunden wird.

Nach Beendigung der inneren Schleife werden die Elemente der Positionen i (Anfang des rechten Teils) und minPos vertauscht (es sei denn, es handelt sich um dasselbe Element).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

Der gezeigte Code unterscheidet sich von der Klasse SelectionSort im GitHub-Repository dadurch, dass er die Schnittstelle SortAlgorithm implementiert, um innerhalb des Test-Frameworks leicht austauschbar zu sein.

Auswahlsortierung Zeitkomplexität

Wir bezeichnen mit n die Anzahl der Elemente, in unserem Beispiel n = 6.

Die beiden verschachtelten Schleifen sind ein Hinweis darauf, dass wir es mit einer Zeitkomplexität* von O(n²) zu tun haben. Dies ist der Fall, wenn beide Schleifen bis zu einem Wert iterieren, der linear mit n zunimmt.

Das ist offensichtlich bei der äußeren Schleife der Fall: Sie zählt bis n-1.

Was ist mit der inneren Schleife?

Sieh dir die folgende Abbildung an:

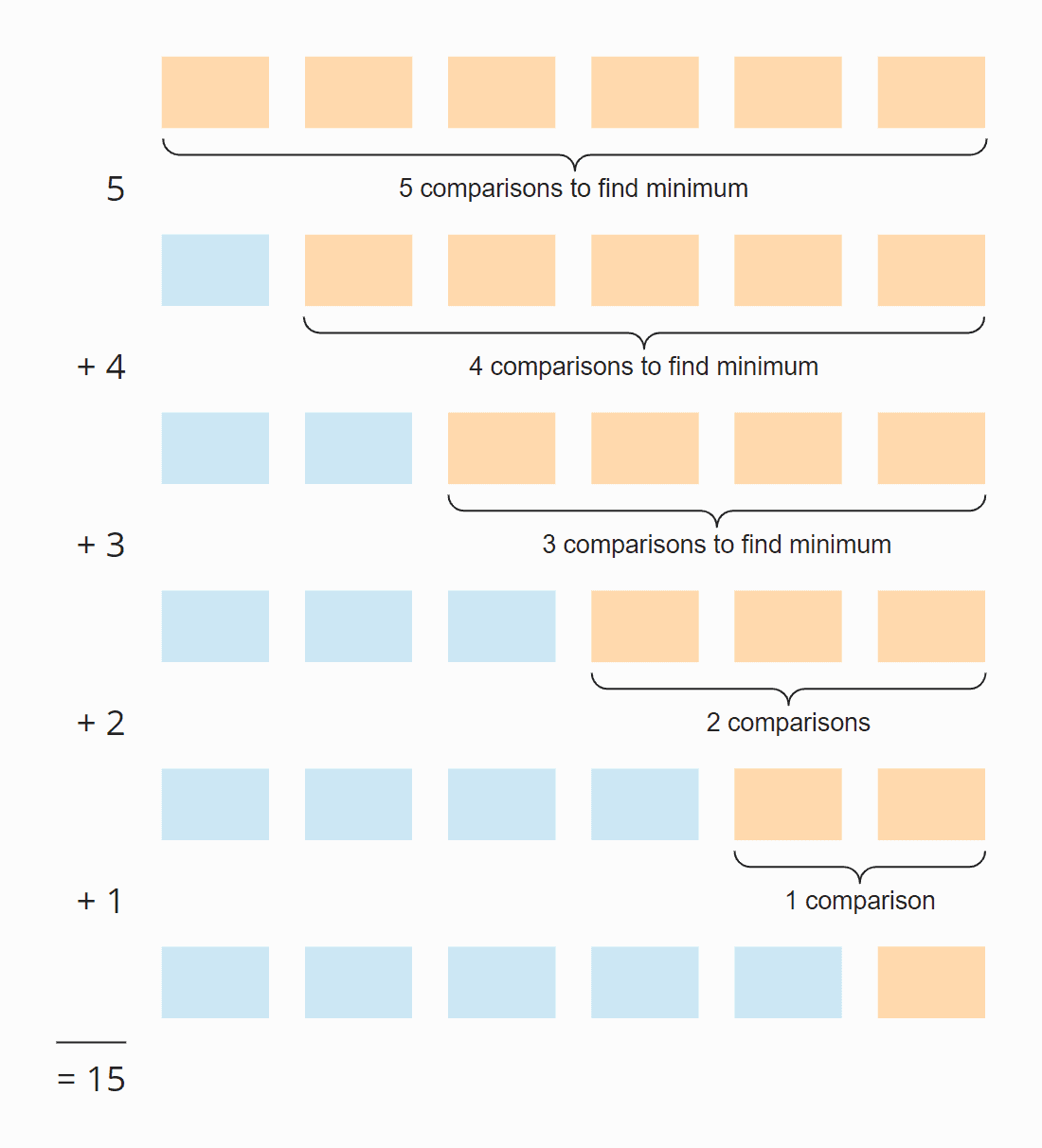
In jedem Schritt ist die Anzahl der Vergleiche um eins geringer als die Anzahl der unsortierten Elemente. Insgesamt sind es 15 Vergleiche – unabhängig davon, ob das Array anfangs sortiert ist oder nicht.

Dies lässt sich auch wie folgt berechnen:

Sechs Elemente mal fünf Schritte; geteilt durch zwei, da im Durchschnitt über alle Schritte die Hälfte der Elemente noch unsortiert ist:

6 × 5 × ½ = 30 × ½ = 15

Ersetzt man 6 durch n, erhält man

n × (n – 1) × ½

Multipliziert ergibt sich:

½ n² – ½ n

Die höchste Potenz von n in diesem Term ist n². Die Zeitkomplexität für die Suche nach dem kleinsten Element ist also O(n²) – auch „quadratische Zeit“ genannt.

Betrachten wir nun das Vertauschen der Elemente. In jedem Schritt (außer dem letzten) wird entweder ein Element vertauscht oder keines, je nachdem, ob das kleinste Element bereits an der richtigen Stelle steht oder nicht. Wir haben also in der Summe maximal n-1 Vertauschungsoperationen, d.h. die Zeitkomplexität von O(n) – auch „lineare Zeit“ genannt.

Für die Gesamtkomplexität ist nur die höchste Komplexitätsklasse von Bedeutung, daher:

Die durchschnittliche, best-case und worst-case Zeitkomplexität von Selection Sort ist: O(n²)

* Die Begriffe „Zeitkomplexität“ und „O-Notation“ werden in diesem Artikel anhand von Beispielen und Diagrammen erklärt.

Laufzeit des Java Selection Sort Beispiels

Genug Theorie! Ich habe ein Testprogramm geschrieben, das die Laufzeit von Selection Sort (und allen anderen in dieser Serie behandelten Sortieralgorithmen) wie folgt misst:

• Die Anzahl der zu sortierenden Elemente verdoppelt sich nach jeder Iteration von ursprünglich 1.024 Elementen auf 536.870.912 (= 229) Elemente. Ein doppelt so großes Array kann in Java nicht erstellt werden.
• Wenn ein Test länger als 20 Sekunden dauert, wird das Array nicht weiter vergrößert.
• Alle Tests werden mit unsortierten sowie auf- und absteigenden vorsortierten Elementen durchgeführt.
• Wir lassen den HotSpot-Compiler den Code mit zwei Aufwärmrunden optimieren. Danach werden die Tests wiederholt, bis der Prozess abgebrochen wird.

Nach jeder Iteration gibt das Programm den Median aller bisherigen Messergebnisse aus.

Hier ist das Ergebnis für Selection Sort nach 50 Iterationen (aus Gründen der Übersichtlichkeit ist dies nur ein Auszug; das vollständige Ergebnis finden Sie hier):

n	unsortiert	aufsteigend	absteigend
…	…	…	…
16.384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Hier die Messungen noch einmal als Diagramm (wobei ich „unsortiert“ und „aufsteigend“ wegen der fast identischen Werte als eine Kurve dargestellt habe):

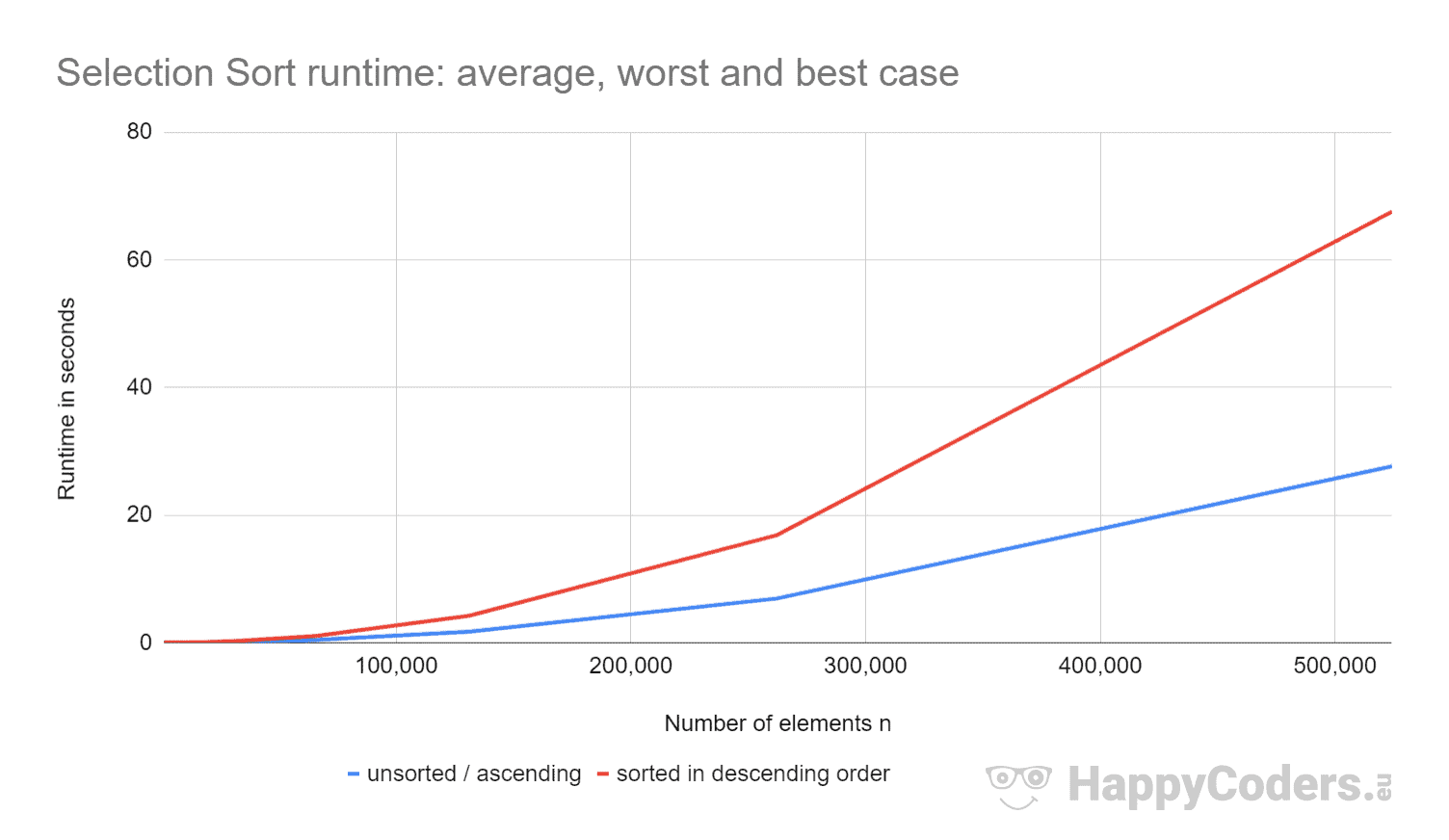
Es ist gut zu sehen, dass

• wenn die Anzahl der Elemente verdoppelt wird, sich die Laufzeit ungefähr vervierfacht – unabhängig davon, ob die Elemente vorher sortiert sind oder nicht. Dies entspricht der erwarteten Zeitkomplexität von O(n²).
• Dass die Laufzeit für aufsteigend sortierte Elemente etwas besser ist als für unsortierte Elemente. Das liegt daran, dass die Vertauschungsoperationen, die – wie oben analysiert – von geringer Bedeutung sind, hier nicht notwendig sind.
• dass die Laufzeit für absteigende sortierte Elemente deutlich schlechter ist als für unsortierte Elemente.

Warum ist das so?

Analyse der Worst-Case-Laufzeit

Theoretisch sollte die Suche nach dem kleinsten Element unabhängig von der Ausgangssituation immer gleich lange dauern. Und die Vertauschungsoperationen sollten bei absteigend sortierten Elementen nur geringfügig mehr sein (bei absteigend sortierten Elementen müsste jedes Element getauscht werden; bei unsortierten Elementen müsste fast jedes Element getauscht werden).

Mit dem Programm CountOperations aus meinem GitHub-Repository können wir die Anzahl der verschiedenen Operationen sehen. Hier sind die Ergebnisse für unsortierte und absteigend sortierte Elemente, zusammengefasst in einer Tabelle:

n	Vergleiche	Swaps unsortiert	Swaps absteigend	minPos/min unsortiert	minPos/min absteigend
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

Aus den Messwerten lässt sich ablesen:

• Bei absteigend sortierten Elementen haben wir – wie erwartet – genauso viele Vergleichsoperationen wie bei unsortierten Elementen, also n × (n-1) / 2.
• Bei unsortierten Elementen haben wir – wie angenommen – fast so viele Vertauschungsoperationen wie Elemente: zum Beispiel gibt es bei 4.096 unsortierten Elementen 4.084 Vertauschungsoperationen. Diese Zahlen ändern sich zufällig von Test zu Test.
• Bei absteigend sortierten Elementen haben wir jedoch nur halb so viele Vertauschungsoperationen wie Elemente! Das liegt daran, dass wir beim Tauschen nicht nur das kleinste Element an die richtige Stelle setzen, sondern auch den jeweiligen Tauschpartner.

Bei acht Elementen haben wir zum Beispiel vier Tauschvorgänge. In den ersten vier Iterationen haben wir jeweils eine und in den Iterationen fünf bis acht keine (trotzdem läuft der Algorithmus bis zum Ende durch):

Weiterhin können wir aus den Messungen ablesen:

• Der Grund, warum Selection Sort bei absteigend sortierten Elementen so viel langsamer ist, liegt in der Anzahl der Zuweisungen lokaler Variablen (minPos und min) bei der Suche nach dem kleinsten Element. Während wir bei 8.192 unsortierten Elementen 69.378 solcher Zuweisungen haben, sind es bei absteigend sortierten Elementen 16.785.407 solcher Zuweisungen – also 242 mal so viele!

Warum dieser große Unterschied?

Analyse der Laufzeit der Suche nach dem kleinsten Element

Für absteigend sortierte Elemente lässt sich die Größenordnung aus der obigen Abbildung ableiten. Die Suche nach dem kleinsten Element beschränkt sich auf das Dreieck der orangefarbenen und orange-blauen Kästen. Im oberen orangefarbenen Teil werden die Zahlen in jedem Kästchen kleiner, im rechten orange-blauen Teil nehmen die Zahlen wieder zu.

Zuweisungsvorgänge finden in jedem orangen Kästchen und dem ersten der orange-blauen Kästchen statt. Die Anzahl der Zuordnungsoperationen für minPos und min ist also bildlich gesprochen etwa „ein Viertel des Quadrats“ – mathematisch genau ist es ¼ n² + n – 1.

Für unsortierte Elemente müssten wir viel tiefer in die Materie eindringen. Das würde nicht nur den Rahmen dieses Artikels, sondern des gesamten Blogs sprengen.

Daher beschränke ich meine Analyse auf ein kleines Demoprogramm, das misst, wie viele minPos/min-Zuweisungen es bei der Suche nach dem kleinsten Element in einem unsortierten Array gibt. Hier sind die Durchschnittswerte nach 100 Iterationen (ein kleiner Auszug; die vollständigen Ergebnisse finden sich hier):

n	Durchschnittszahl der minPos/min Zuweisungen
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Hier als Diagramm mit logarithmischer x-Achse:

Das Diagramm zeigt sehr schön, dass wir logarithmisches Wachstum haben, d.h., bei jeder Verdoppelung der Anzahl der Elemente nimmt die Anzahl der Zuweisungen nur um einen konstanten Wert zu. Wie gesagt, ich werde nicht näher auf die mathematischen Hintergründe eingehen.

Das ist der Grund, warum diese minPos/min Zuweisungen in unsortierten Arrays von geringer Bedeutung sind.

Weitere Eigenschaften von Selection Sort

In den folgenden Abschnitten werde ich die Raumkomplexität, Stabilität und Parallelisierbarkeit von Selection Sort diskutieren.

Platzkomplexität von Selection Sort

Die Platzkomplexität von Selection Sort ist konstant, da wir außer den Schleifenvariablen i und j und den Hilfsvariablen length, minPos und min keinen zusätzlichen Speicherplatz benötigen.

Das heißt, egal wie viele Elemente wir sortieren – zehn oder zehn Millionen – wir brauchen immer nur diese fünf zusätzlichen Variablen. Wir notieren die konstante Zeit als O(1).

Stabilität der Auswahlsortierung

Die Auswahlsortierung erscheint auf den ersten Blick stabil: Wenn der unsortierte Teil mehrere Elemente mit demselben Schlüssel enthält, sollte das erste zuerst an den sortierten Teil angehängt werden.

Aber der Schein trügt. Denn durch das Vertauschen zweier Elemente im zweiten Teilschritt des Algorithmus kann es passieren, dass bestimmte Elemente im unsortierten Teil nicht mehr die ursprüngliche Reihenfolge haben. Das wiederum führt dazu, dass sie im sortierten Teil nicht mehr in der ursprünglichen Reihenfolge erscheinen.

Ein Beispiel lässt sich sehr einfach konstruieren. Nehmen wir an, wir haben zwei verschiedene Elemente mit dem Schlüssel 2 und eines mit dem Schlüssel 1, die wie folgt angeordnet sind, und sortieren sie dann mit Selection Sort:

Im ersten Schritt werden das erste und das letzte Element vertauscht. So landet das Element „ZWEI“ hinter dem Element „zwei“ – die Reihenfolge der beiden Elemente ist vertauscht.

Im zweiten Schritt vergleicht der Algorithmus die beiden hinteren Elemente. Beide haben den gleichen Schlüssel, 2. Es wird also kein Element vertauscht.

Im dritten Schritt bleibt nur noch ein Element übrig; dieses gilt automatisch als sortiert.

Die beiden Elemente mit dem Schlüssel 2 sind also in ihrer ursprünglichen Reihenfolge vertauscht worden – der Algorithmus ist instabil.

Stabile Variante der Auswahlsortierung

Die Auswahlsortierung kann stabil gemacht werden, indem im zweiten Schritt nicht das kleinste Element mit dem ersten vertauscht wird, sondern alle Elemente zwischen dem ersten und dem kleinsten Element um eine Position nach rechts verschoben werden und das kleinste Element am Anfang eingefügt wird.

Auch wenn die Zeitkomplexität durch diese Änderung gleich bleibt, führen die zusätzlichen Verschiebungen zu einer deutlichen Leistungsverschlechterung, zumindest wenn wir ein Array sortieren.

Bei einer verknüpften Liste könnte das Ausschneiden und Einfügen des zu sortierenden Elements ohne nennenswerte Leistungseinbußen erfolgen.

Parallelisierbarkeit der Auswahlsortierung

Wir können die äußere Schleife nicht parallelisieren, da sie den Inhalt des Arrays in jeder Iteration ändert.

Die innere Schleife (Suche nach dem kleinsten Element) kann parallelisiert werden, indem das Array geteilt wird, in jedem Unterarray parallel nach dem kleinsten Element gesucht wird und die Zwischenergebnisse zusammengeführt werden.

Selection Sort vs. Insertion Sort

Welcher Algorithmus ist schneller, Selection Sort oder Insertion Sort?

Lassen Sie uns die Messungen aus meinen Java-Implementierungen vergleichen.

Ich lasse den besten Fall weg. Bei Insertion Sort ist die Zeitkomplexität im besten Fall O(n) und dauerte weniger als eine Millisekunde für bis zu 524.288 Elemente. Im besten Fall ist Insertion Sort also für eine beliebige Anzahl von Elementen um Größenordnungen schneller als Selection Sort.

n	Auswahlsortierung unsortiert	Einfügungssortierung unsortiert	Auswahlsortierung absteigend	Einfügungssortierung absteigend
…	…	…	…	…
16.384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65.536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

Und noch einmal als Diagramm:

Insertion Sort ist also nicht nur im besten Fall, sondern auch im durchschnittlichen und im schlechtesten Fall schneller als Selection Sort.

Der Grund dafür ist, dass Insertion Sort im Durchschnitt halb so viele Vergleiche benötigt. Zur Erinnerung: Bei Insertion Sort haben wir Vergleiche und Verschiebungen, die im Durchschnitt die Hälfte der sortierten Elemente betreffen; bei Selection Sort müssen wir in jedem Schritt nach dem kleinsten Element in allen unsortierten Elementen suchen.

Selection Sort hat deutlich weniger Schreiboperationen, so dass Selection Sort schneller sein kann, wenn Schreiboperationen teuer sind. Dies ist bei sequentiellen Schreibvorgängen in Arrays nicht der Fall, da diese meist im CPU-Cache durchgeführt werden.

In der Praxis wird Selection Sort daher fast nie verwendet.

Zusammenfassung

Selection Sort ist ein einfach zu implementierender und in seiner typischen Implementierung instabiler Sortieralgorithmus mit einer durchschnittlichen, Best-Case- und Worst-Case-Zeitkomplexität von O(n²).

Selection Sort ist langsamer als Insertion Sort, weshalb er in der Praxis nur selten verwendet wird.

Weitere Sortieralgorithmen finden Sie in dieser Übersicht über alle Sortieralgorithmen und deren Eigenschaften im ersten Teil der Artikelserie.

Wenn Ihnen der Artikel gefallen hat, können Sie ihn gerne über einen der Share-Buttons am Ende teilen. Möchten Sie per E-Mail informiert werden, wenn ich einen neuen Artikel veröffentliche? Dann nutzen Sie das folgende Formular, um meinen Newsletter zu abonnieren.