Eine Gleichung in Form des Steigungsabschnitts wird geschrieben als
$$y=mx+b$$
Wobei m die Steigung der Geraden und b der y-Achsenabschnitt ist. Du kannst diese Gleichung verwenden, um eine Gleichung zu schreiben, wenn du die Steigung und den y-Achsenabschnitt kennst.
Beispiel
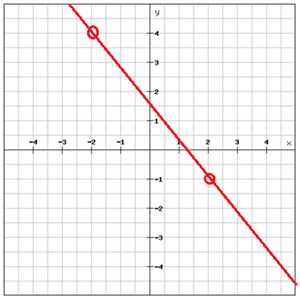
Finde die Gleichung der Geraden
Wähle zwei Punkte, die auf der Geraden liegen
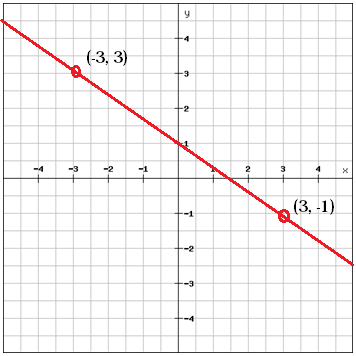
Berechne die Steigung zwischen den beiden Punkten
$$m=\frac{y_{2}\, -y_{1}}{x_{2}\, -x_{1}}=\frac{\left (-1 \right )-3}{3-\left ( -3 \right )}=\frac{-4}{6}=\frac{-2}{3}$$
Wir können den b-Wert finden, den y-Achsenabschnitt, indem wir den Graphen betrachten
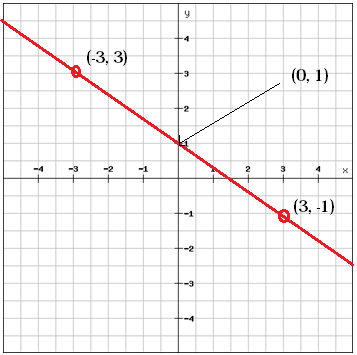
b = 1
Wir haben einen Wert für m und einen Wert für b. Damit haben wir die lineare Funktion
$$y=-\frac{2}{3}x+1$$
In vielen Fällen ist der Wert von b nicht so leicht abzulesen. In diesen Fällen, oder wenn man sich nicht sicher ist, ob die Gerade die y-Achse in diesem bestimmten Punkt tatsächlich schneidet, kann man b berechnen, indem man die Gleichung für b löst und dann x und y durch einen der beiden Punkte ersetzt.
Wir können das anhand des obigen Beispiels veranschaulichen. Wir haben die beiden Punkte (-3, 3) und (3, -1). Aus diesen beiden Punkten haben wir die Steigung berechnet
$$m=-\frac{2}{3}$$
Das gibt uns die Gleichung
$$y=-\frac{2}{3}x+b$$
Daraus können wir die Gleichung für b lösen
$$b=y+\frac{2}{3}x$$
Und wenn wir die Werte aus unserem ersten Punkt einsetzen (-3, 3) erhalten wir
$$b=3+\frac{2}{3}\cdot \links ( -3 \rechts )=3+\links ( -2 \rechts )=1$$
Wenn wir diesen Wert für b in die Gleichung einsetzen, erhalten wir
$$y=-\frac{2}{3}x+1$$
Das ist die gleiche Gleichung, die wir erhalten haben, als wir den y-Achsenabschnitt aus dem Graphen abgelesen haben.
Zusammenfassend kann man sagen, wie man eine lineare Gleichung mit Hilfe der Steigungs-Abschnitt-Form schreibt:
- Bestimme die Steigung m. Dies kann man tun, indem man die Steigung zwischen zwei bekannten Punkten der Linie mit Hilfe der Steigungsformel berechnet.
- Ermittle den y-Abschnitt. Dies kann geschehen, indem man die Steigung und die Koordinaten eines Punktes (x, y) auf der Geraden in die Steigungs-Achsenformel einsetzt und dann für b löst.
Wenn man sowohl m als auch b hat, kann man sie einfach an ihrer jeweiligen Position in die Gleichung einsetzen.
Videolektion
Finden Sie die Gleichung zum Graphen