Biographie
Johannes Kepler ist heute vor allem für die Entdeckung der drei Gesetze der Planetenbewegung bekannt, die seinen Namen tragen (veröffentlicht 1609 und 1619). Er leistete auch wichtige Arbeit in der Optik (1604, 1611), entdeckte zwei neue regelmäßige Polyeder (1619), gab die erste mathematische Behandlung der engen Packung gleicher Kugeln (was zu einer Erklärung der Form der Zellen einer Bienenwabe führte, 1611), lieferte den ersten Beweis für die Funktionsweise von Logarithmen (1624) und entwickelte eine Methode zur Bestimmung des Volumens von Rotationskörpern, die (im Nachhinein!) als Beitrag zur Entwicklung der Infinitesimalrechnung angesehen werden kann (1615, 1616). Darüber hinaus berechnete er die genauesten astronomischen Tabellen, die bis dahin bekannt waren, und deren anhaltende Genauigkeit trug wesentlich dazu bei, die Wahrheit der heliozentrischen Astronomie zu begründen (Rudolphinische Tabellen, Ulm, 1627).
Eine große Menge von Keplers Korrespondenz ist erhalten. Viele seiner Briefe sind fast das Äquivalent einer wissenschaftlichen Arbeit (es gab noch keine wissenschaftlichen Zeitschriften), und die Korrespondenten scheinen sie aufbewahrt zu haben, weil sie interessant waren. Folglich wissen wir ziemlich viel über Keplers Leben und auch über seinen Charakter. Dies ist zum Teil der Grund dafür, dass Kepler eine gewisse Karriere als mehr oder weniger fiktive Figur gemacht hat (siehe historiographische Anmerkung unten).
Kindheit
Kepler wurde in der kleinen Stadt Weil der Stadt in Schwaben geboren und zog 1576 mit seinen Eltern ins nahe gelegene Leonberg. Sein Vater war ein Söldner und seine Mutter die Tochter eines Gastwirts. Johannes war ihr erstes Kind. Sein Vater verließ die Heimat zum letzten Mal, als Johannes fünf Jahre alt war, und man nimmt an, dass er im Krieg in den Niederlanden gefallen ist. Als Kind lebte Kepler mit seiner Mutter im Gasthaus seines Großvaters. Er erzählt uns, dass er im Gasthaus als Kellner aushalf. Man kann sich vorstellen, dass die Gäste manchmal über die ungewöhnlichen Rechenkünste des Kindes verwirrt waren.
Keplers frühe Ausbildung erfolgte in einer örtlichen Schule und dann in einem nahegelegenen Priesterseminar, von dem aus er sich mit der Absicht, ordiniert zu werden, an der Universität Tübingen einschrieb, damals (wie heute) eine Bastion der lutherischen Orthodoxie.
Keplers Ansichten
Sein ganzes Leben lang war Kepler ein zutiefst religiöser Mensch. Alle seine Schriften enthalten zahlreiche Hinweise auf Gott, und er sah seine Arbeit als Erfüllung seiner christlichen Pflicht, die Werke Gottes zu verstehen. Da der Mensch, wie Kepler glaubte, nach dem Bilde Gottes geschaffen wurde, war er eindeutig in der Lage, das von ihm geschaffene Universum zu verstehen. Außerdem war Kepler davon überzeugt, dass Gott das Universum nach einem mathematischen Plan erschaffen hatte (ein Glaube, der sich in den Werken von Platon findet und mit Pythagoras in Verbindung gebracht wird). Da zu dieser Zeit allgemein anerkannt war, dass die Mathematik eine sichere Methode zur Erlangung von Wahrheiten über die Welt bot (Euklids allgemeine Begriffe und Postulate wurden als tatsächlich wahr angesehen), haben wir hier eine Strategie zum Verständnis des Universums. Da einige Autoren Kepler einen Namen für Irrationalität gegeben haben, ist es erwähnenswert, dass diese eher hoffnungsvolle Erkenntnistheorie in der Tat sehr weit von der Überzeugung des Mystikers entfernt ist, dass die Dinge nur auf eine ungenaue Weise verstanden werden können, die sich auf Erkenntnisse stützt, die nicht der Vernunft unterliegen. Zwar dankt Kepler Gott immer wieder dafür, dass er ihm Einsichten geschenkt hat, aber die Einsichten werden als rational dargestellt.
Universitäre Ausbildung
Zu dieser Zeit war es üblich, dass alle Studenten an einer Universität Kurse über „Mathematik“ besuchten. Dazu gehörten im Prinzip die vier mathematischen Wissenschaften: Arithmetik, Geometrie, Astronomie und Musik. Was gelehrt wurde, scheint jedoch von der jeweiligen Universität abhängig gewesen zu sein. In Tübingen wurde Kepler von einem der führenden Astronomen seiner Zeit, Michael Mästlin (1550 – 1631), in Astronomie unterrichtet. Die Astronomie, die auf dem Lehrplan stand, war natürlich die geozentrische Astronomie, d. h. die aktuelle Version des ptolemäischen Systems, in dem sich alle sieben Planeten – Mond, Merkur, Venus, Sonne, Mars, Jupiter und Saturn – um die Erde bewegen, wobei ihre Positionen gegenüber den Fixsternen durch die Kombination von Kreisbewegungen berechnet werden. Dieses System entsprach mehr oder weniger den heutigen (aristotelischen) Vorstellungen von Physik, auch wenn es gewisse Schwierigkeiten gab, wie z. B. die Frage, ob man eine Kreisbewegung, die sich nicht einheitlich um ihren eigenen Mittelpunkt, sondern um einen anderen Punkt (einen so genannten „Äquanten“) drehte, als „gleichförmig“ (und damit als offensichtlich ewig annehmbar) betrachten konnte. Im Großen und Ganzen scheinen sich die Astronomen (die sich als „Mathematiker“ verstanden) jedoch damit begnügt zu haben, die Positionen der Planeten zu berechnen und es den Naturphilosophen zu überlassen, sich darüber Gedanken zu machen, ob die mathematischen Modelle den physikalischen Mechanismen entsprachen. Kepler nahm diese Haltung nicht ein. In seinem frühesten veröffentlichten Werk (1596) schlägt er vor, die tatsächlichen Bahnen der Planeten zu betrachten und nicht die Kreise, mit denen sie konstruiert wurden.
In Tübingen studierte Kepler nicht nur Mathematik, sondern auch Griechisch und Hebräisch (beides notwendig, um die heiligen Schriften in ihren Originalsprachen zu lesen). Der Unterricht fand in Latein statt. Am Ende seines ersten Jahres bekam Kepler für alles außer Mathematik eine Eins. Wahrscheinlich wollte Mästlin ihm sagen, dass er es besser kann, denn Kepler gehörte zu den ausgewählten Schülern, denen er fortgeschrittenere Astronomie beibringen wollte, indem er sie in das neue, heliozentrische kosmologische System von Kopernikus einführte. Von Mästlin erfuhr Kepler, dass die Vorrede zu „Über die Umdrehungen“, in der erklärt wird, dass es sich „nur um Mathematik“ handelt, nicht von Kopernikus stammte. Kepler scheint fast sofort akzeptiert zu haben, dass das kopernikanische System physikalisch wahr ist; seine Gründe dafür werden im Zusammenhang mit seinem ersten kosmologischen Modell diskutiert (siehe unten).
Es scheint, dass es schon in Keplers Studentenzeit Anzeichen dafür gab, dass seine religiösen Überzeugungen nicht ganz mit dem in Tübingen herrschenden orthodoxen Luthertum übereinstimmten, das in der Confessio Augustana Ⓣ formuliert wurde. Keplers Probleme mit dieser protestantischen Orthodoxie betrafen die vermeintliche Beziehung zwischen Materie und „Geist“ (einer nicht-materiellen Entität) in der Lehre von der Eucharistie. Dies knüpft insofern an Keplers Astronomie an, als er offenbar ähnliche intellektuelle Schwierigkeiten hatte zu erklären, wie die „Kraft“ der Sonne auf die Planeten wirken konnte. In seinen Schriften legt Kepler seine Ansichten gerne offen dar – was für Historiker sehr praktisch ist. Im wirklichen Leben scheint es wahrscheinlich, dass eine ähnliche Tendenz zur Offenheit die Behörden in Tübingen dazu brachte, begründete Zweifel an seiner religiösen Rechtgläubigkeit zu hegen. Diese mögen erklären, warum Mästlin Kepler dazu überredete, seine Pläne für die Ordination aufzugeben und stattdessen eine Stelle als Mathematiklehrer in Graz anzutreten. Die religiöse Intoleranz verschärfte sich in den folgenden Jahren. Kepler wurde 1612 exkommuniziert. Dies bereitete ihm viel Kummer, doch trotz seines (damals) relativ hohen gesellschaftlichen Ansehens als kaiserlicher Mathematiker gelang es ihm nie, die Aufhebung des Banns zu erreichen.
Keplers erstes kosmologisches Modell (1596)
Anstatt der sieben Planeten der geozentrischen Standardastronomie hatte das kopernikanische System nur sechs, da der Mond zu einem der Astronomie bis dahin unbekannten Körper geworden war, den Kepler später als „Satellit“ bezeichnete (eine Bezeichnung, die er 1610 für die von Galilei entdeckten Monde, die den Jupiter umkreisten, prägte und die wörtlich „Begleiter“ bedeutet). Warum sechs Planeten?
Außerdem gab es in der geozentrischen Astronomie keine Möglichkeit, anhand von Beobachtungen die relativen Größen der Planetenkugeln zu bestimmen; man nahm einfach an, dass sie sich berühren. Dies schien keiner Erklärung zu bedürfen, denn es passte gut zu dem Glauben der Naturphilosophen, dass das ganze System aus der Bewegung der äußersten Sphäre, einer (oder vielleicht zwei) jenseits der Sphäre der „Fixsterne“ (derjenigen, deren Muster die Sternbilder bildeten), jenseits der Sphäre des Saturn, gedreht wurde. Im kopernikanischen System erlaubte es die Tatsache, dass die jährliche Komponente jeder Planetenbewegung ein Spiegelbild der jährlichen Bewegung der Erde war, anhand von Beobachtungen die Größe der Bahn jedes Planeten zu berechnen, und es stellte sich heraus, dass es zwischen den Planeten riesige Räume gab. Warum gerade diese Zwischenräume?
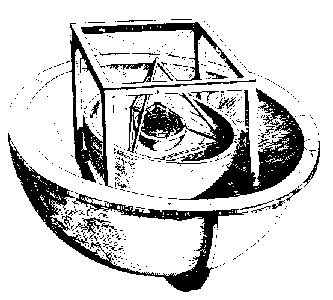
Keplers Antwort auf diese Fragen, beschrieben in seinem Mysterium cosmographicum Ⓣ, Tübingen, 1596, erscheint dem Leser des zwanzigsten Jahrhunderts bizarr (siehe die Abbildung rechts). Er schlug vor, dass, wenn eine Kugel so gezeichnet würde, dass sie die Innenseite der Bahn des Saturn berührt, und ein Würfel in die Kugel eingeschrieben wäre, die in diesen Würfel eingeschriebene Kugel die Kugel wäre, die die Bahn des Jupiter umschreibt. Würde man dann ein regelmäßiges Tetraeder in die Sphäre einzeichnen, die die Bahn des Jupiters beschreibt, so wäre die Innenseite des Tetraeders die Sphäre, die die Bahn des Mars umschreibt, und so weiter, wobei das regelmäßige Dodekaeder zwischen Mars und Erde, das regelmäßige Ikosaeder zwischen Erde und Venus und das regelmäßige Oktaeder zwischen Venus und Merkur liegt. Dies erklärt die Anzahl der Planeten perfekt: Es gibt nur fünf konvexe regelmäßige Körper (wie in Euklids Elementen, Buch 13, nachgewiesen). Außerdem stimmt es überzeugend mit den von Kopernikus abgeleiteten Größen der Bahnen überein, wobei der größte Fehler weniger als 10 % beträgt (was für ein kosmologisches Modell auch heute noch spektakulär gut ist). Kepler drückte sich nicht in Form von prozentualen Fehlern aus, und sein Modell ist in der Tat das erste mathematische kosmologische Modell, aber es ist leicht zu verstehen, warum er glaubte, dass die Beobachtungen seine Theorie unterstützten.
Kepler sah seine kosmologische Theorie als Beweis für die kopernikanische Theorie. Bevor er seine eigene Theorie vorstellte, führte er Argumente an, um die Plausibilität der kopernikanischen Theorie selbst zu belegen. Die Vorteile der kopernikanischen Theorie gegenüber der geozentrischen Theorie liegen nach Keplers Ansicht in ihrer größeren Erklärungskraft. So kann die kopernikanische Theorie beispielsweise erklären, warum Venus und Merkur nie sehr weit von der Sonne entfernt sind (sie liegen zwischen Erde und Sonne), während es in der geozentrischen Theorie keine Erklärung für diese Tatsache gibt. Kepler listet im ersten Kapitel des Mysterium cosmographicum Ⓣ neun solcher Fragen auf.
Kepler führte diese Arbeit durch, während er in Graz lehrte, aber das Buch wurde in Tübingen von Mästlin durch die Presse gebracht. Die Übereinstimmung mit den aus der Beobachtung abgeleiteten Werten war nicht exakt, und Kepler hoffte, dass bessere Beobachtungen die Übereinstimmung verbessern würden, also schickte er ein Exemplar des Mysterium cosmographicum an einen der führenden Beobachtungsastronomen seiner Zeit, Tycho Brahe (1546 – 1601). Tycho, der damals in Prag (der damaligen Hauptstadt des Heiligen Römischen Reiches) arbeitete, hatte nämlich bereits an Mästlin geschrieben und nach einem mathematischen Assistenten gesucht. Kepler bekam die Stelle.
Der „Krieg mit dem Mars“
Natürlich waren Tychos Prioritäten nicht die gleichen wie die von Kepler, und Kepler fand sich bald in der Arbeit an dem hartnäckigen Problem der Umlaufbahn des Mars wieder. Er arbeitete auch nach Tychos Tod (1601) weiter an diesem Problem, und Kepler wurde sein Nachfolger als kaiserlicher Mathematiker. Konventionell waren die Bahnen aus Kreisen zusammengesetzt, und es waren nur wenige Beobachtungswerte erforderlich, um die relativen Radien und Positionen der Kreise zu bestimmen. Tycho hatte eine große Anzahl von Beobachtungen gemacht, und Kepler beschloss, diese bestmöglich zu nutzen. Im Wesentlichen standen ihm so viele Beobachtungen zur Verfügung, dass er, sobald er eine mögliche Umlaufbahn konstruiert hatte, diese mit weiteren Beobachtungen abgleichen konnte, bis eine zufriedenstellende Übereinstimmung erreicht war. Kepler kam zu dem Schluss, dass die Bahn des Mars eine Ellipse mit der Sonne in einem ihrer Brennpunkte ist (ein Ergebnis, das, wenn es auf alle Planeten ausgedehnt wird, heute als „Keplersches Erstes Gesetz“ bezeichnet wird), und dass eine Linie, die den Planeten mit der Sonne verbindet, in gleichen Zeiten gleiche Flächen abtastet, während der Planet seine Bahn beschreibt („Keplersches Zweites Gesetz“), d. h. die Fläche wird als Maß für die Zeit verwendet. Nachdem diese Arbeit in Astronomia nova veröffentlicht wurde, … Ⓣ, Heidelberg, 1609, fand Kepler Bahnen für die anderen Planeten und stellte damit fest, dass die beiden Gesetze auch für sie gelten. Beide Gesetze beziehen sich auf die Bewegung des Planeten in Bezug auf die Sonne; Keplers Kopernikanismus war entscheidend für seine Argumentation und seine Schlussfolgerungen.
Der eigentliche Prozess der Berechnung für den Mars war immens mühsam – es gibt fast tausend erhaltene Folioblätter mit Berechnungen – und Kepler selbst bezeichnet diese Arbeit als „meinen Krieg mit dem Mars“, aber das Ergebnis war eine Bahn, die mit modernen Ergebnissen so genau übereinstimmt, dass der Vergleich säkulare Veränderungen der Bahn seit Keplers Zeit berücksichtigen muss.
Beobachtungsfehler
Für Keplers Methode, mögliche Bahnen mit Beobachtungen abzugleichen, war es entscheidend, dass er eine Vorstellung davon hatte, was als ausreichende Übereinstimmung akzeptiert werden sollte. Daraus ergibt sich die erste ausdrückliche Verwendung des Begriffs des Beobachtungsfehlers. Kepler verdankt diesen Begriff möglicherweise zumindest teilweise Tycho, der die Leistung seiner Instrumente eingehend überprüfte (siehe die Biographie von Brahe).
Optik und der neue Stern von 1604
Die Arbeit am Mars war 1605 im Wesentlichen abgeschlossen, aber die Veröffentlichung des Buches verzögerte sich. In der Zwischenzeit beschäftigte sich Kepler mit dem unterschiedlichen scheinbaren Durchmesser des Mondes bei direkter Beobachtung und bei der Beobachtung mit einer Camera obscura und entwickelte die erste korrekte mathematische Theorie der Camera obscura sowie die erste korrekte Erklärung der Funktionsweise des menschlichen Auges mit einem auf dem Kopf stehenden Bild auf der Netzhaut. Diese Ergebnisse wurden in Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Frankfurt, 1604 veröffentlicht. Er schrieb auch über den Neuen Stern von 1604, der heute gewöhnlich als „Keplers Supernova“ bezeichnet wird, lehnte zahlreiche Erklärungen ab und bemerkte an einer Stelle, dass dieser Stern natürlich nur eine besondere Schöpfung sein könnte, „aber bevor wir dazu kommen, denke ich, sollten wir alles andere versuchen“ De stella nova Ⓣ, Prag, 1606, Kapitel 22, KGW 1, S. 257, Zeile 23.
Nachdem Galilei mit Hilfe des Fernrohrs die Jupitermonde entdeckt hatte, die er in seinem Siderischen Boten (Venedig, 1610) veröffentlicht hatte, worauf Kepler eine begeisterte Antwort geschrieben hatte (1610), schrieb Kepler eine Studie über die Eigenschaften von Linsen (die erste derartige Arbeit über Optik), in der er eine neue Konstruktion eines Fernrohrs mit zwei konvexen Linsen vorstellte (Dioptrice, Prag, 1611). Diese Konstruktion, bei der das endgültige Bild invertiert ist, war so erfolgreich, dass sie heute gewöhnlich nicht als Kepler-Fernrohr, sondern einfach als astronomisches Fernrohr bezeichnet wird.
Aufbruch von Prag nach Linz
Keplers Jahre in Prag waren relativ friedlich und wissenschaftlich äußerst produktiv. Selbst wenn die Dinge schlecht liefen, scheint er sich durch äußere Umstände nie von seiner Arbeit abhalten lassen zu haben. Ende 1611 begannen die Dinge sehr schlecht zu laufen. Zunächst starb sein sieben Jahre alter Sohn. Kepler schrieb an einen Freund, dass dieser Tod besonders schwer zu ertragen war, weil das Kind ihn so sehr an sich selbst in diesem Alter erinnerte. Dann starb Keplers Frau. Dann musste der gesundheitlich angeschlagene Kaiser Rudolf zugunsten seines Bruders Matthias abdanken, der wie Rudolf katholisch war, aber (im Gegensatz zu Rudolf) nicht an die Toleranz gegenüber den Protestanten glaubte. Kepler musste Prag verlassen. Bevor er abreiste, ließ er den Leichnam seiner Frau in das Grab des Sohnes überführen und schrieb eine lateinische Grabinschrift für sie. Er und seine verbliebenen Kinder zogen nach Linz (heute in Österreich).
Ehe und Weinfässer
Kepler scheint seine erste Frau Barbara aus Liebe geheiratet zu haben (obwohl die Ehe durch einen Makler vermittelt wurde). Die zweite Ehe, 1613, war eine Frage der praktischen Notwendigkeit; er brauchte jemanden, der sich um die Kinder kümmerte. Keplers neue Frau Susanna erhielt einen Crashkurs in Keplers Charakter: In der Widmung des Buches heißt es, dass ihm bei der Hochzeitsfeier aufgefallen sei, dass das Volumen der Weinfässer mit Hilfe eines schräg durch das Spundloch gesteckten Stabs geschätzt wurde, und er sich fragte, wie das funktionieren könnte. Das Ergebnis war eine Studie über die Volumina von Rotationskörpern Nova stereometria doliorum … Ⓣ, Linz, 1615, in der Kepler, aufbauend auf den Arbeiten von Archimedes, eine Auflösung in „Unteilbares“ verwendete. Diese Methode wurde später von Bonaventura Cavalieri (ca. 1598 – 1647) entwickelt und gehört zu den Vorfahren der Infinitesimalrechnung.
Die Harmonie der Welt
Keplers Hauptaufgabe als kaiserlicher Mathematiker war es, astronomische Tabellen auf der Grundlage von Tychos Beobachtungen zu verfassen, aber eigentlich wollte er die Harmonie der Welt schreiben, die seit 1599 als Weiterentwicklung seines Mysteriums des Kosmos geplant war. Dieses zweite Werk über Kosmologie (Harmonices mundi libri V Ⓣ, Linz, 1619) präsentiert ein ausgefeilteres mathematisches Modell als das frühere, obwohl die Polyeder immer noch vorhanden sind. Die Mathematik in diesem Werk umfasst die erste systematische Behandlung von Tessellationen, einen Beweis, dass es nur dreizehn konvexe einheitliche Polyeder (die archimedischen Körper) gibt, und die erste Darstellung von zwei nicht-konvexen regelmäßigen Polyedern (alle in Buch 2). Die Harmonie der Welt enthält auch das so genannte „Dritte Keplersche Gesetz“, das besagt, dass für zwei beliebige Planeten das Verhältnis der Quadrate ihrer Perioden gleich dem Verhältnis der Kuben der mittleren Radien ihrer Umlaufbahnen ist. Von Anfang an hatte Kepler nach einer Regel gesucht, die die Größe der Bahnen mit den Perioden in Beziehung setzt, aber es gab keine langsame Reihe von Schritten zu diesem Gesetz, wie es bei den beiden anderen der Fall war. Obwohl das Dritte Gesetz in einigen der letzten Abschnitte der gedruckten Version der Harmonie der Welt eine wichtige Rolle spielt, wurde es erst entdeckt, als das Werk bereits im Druck war. Kepler nahm in letzter Minute Überarbeitungen vor. Er selbst erzählt die Geschichte des letztendlichen Erfolgs:
…und wenn man den genauen Zeitpunkt wissen will, so wurde sie am 8. März dieses Jahres eintausendsechshundertachtzehn gedanklich erdacht, aber auf unglückliche Weise der Berechnung unterworfen und daher als falsch verworfen, und endlich am 15. Mai zurückkehrend und eine neue Angriffslinie annehmend, stürmte sie die Dunkelheit meines Geistes. Die Kombination aus meiner siebzehnjährigen Arbeit an den Beobachtungen von Brahe und der vorliegenden Studie, die zusammenwirkten, war eine so starke Stütze, dass ich zuerst glaubte, zu träumen und meine Schlussfolgerung unter meinen Grundvoraussetzungen anzunehmen. Aber es ist absolut sicher und genau, dass „das Verhältnis zwischen den periodischen Zeiten zweier Planeten genau das sesquialterate Verhältnis ihrer mittleren Abstände ist …“
(Harmonice mundi Buch 5, Kapitel 3, trans. Aiton, Duncan und Field, S. 411).
Hexereiprozess
Während Kepler an seiner Harmonie der Welt arbeitete, wurde seine Mutter der Hexerei angeklagt. Er nahm die Hilfe der juristischen Fakultät in Tübingen in Anspruch. Katharina Kepler wurde schließlich freigelassen, zumindest teilweise aufgrund technischer Einwände, die sich daraus ergaben, dass die Behörden bei der Anwendung der Folter nicht die korrekten rechtlichen Verfahren befolgten. Die erhaltenen Dokumente sind erschreckend. Kepler arbeitete jedoch weiter. In der Kutsche, auf seiner Reise nach Württemberg, um seine Mutter zu verteidigen, las er ein musiktheoretisches Werk von Vincenzo Galilei (ca. 1520 – 1591, Galileis Vater), auf das in Die Harmonie der Welt mehrfach Bezug genommen wird.
Astronomische Tabellen
Das Rechnen mit Tabellen, das normale Geschäft eines Astronomen, war immer mit schwerer Arithmetik verbunden. Kepler war dementsprechend erfreut, als er 1616 auf Napiers Werk über Logarithmen (1614 veröffentlicht) stieß. Mästlin wies ihn jedoch prompt darauf hin, dass es sich für einen ernsthaften Mathematiker nicht gezieme, sich über eine bloße Rechenhilfe zu freuen, und dass es unklug sei, den Logarithmen zu vertrauen, da niemand ihre Funktionsweise verstehe. (Ähnliches wurde Anfang der 1960er Jahre über Computer gesagt.) Keplers Antwort auf den zweiten Einwand bestand darin, einen Beweis für die Funktionsweise von Logarithmen zu veröffentlichen, der sich auf eine tadellos seriöse Quelle stützte: Euklid’s Elemente Buch 5. Kepler berechnete Tabellen mit achtstelligen Logarithmen, die mit den Rudolphinischen Tafeln (Ulm, 1628) veröffentlicht wurden. Die astronomischen Tabellen verwendeten nicht nur Tychos Beobachtungen, sondern auch Keplers erste beiden Gesetze. Alle astronomischen Tabellen, die neue Beobachtungen nutzten, waren in den ersten Jahren nach ihrer Veröffentlichung genau. Das Bemerkenswerte an den Rudolphinischen Tafeln war, dass sie sich über Jahrzehnte hinweg als genau erwiesen. Und mit den Jahren wurde die anhaltende Genauigkeit der Tabellen natürlich als ein Argument für die Richtigkeit der Keplerschen Gesetze und damit für die Richtigkeit der heliozentrischen Astronomie angesehen. Keplers Erfüllung seiner langweiligen offiziellen Aufgabe als kaiserlicher Mathematiker führte zur Erfüllung seines sehnlichsten Wunsches, zur Etablierung des Kopernikanismus beizutragen.
Wallenstein
Zum Zeitpunkt der Veröffentlichung der Rudolfinischen Tafeln arbeitete Kepler eigentlich nicht mehr für den Kaiser (er hatte Linz 1626 verlassen), sondern für Albrecht von Wallenstein (1583 – 1632), einen der wenigen erfolgreichen Heerführer im Dreißigjährigen Krieg (1618 – 1648).
Wallenstein erwartete von Kepler, ebenso wie Kaiser Rudolf, astrologisch fundierte Ratschläge. Kepler musste natürlich gehorchen, weist aber immer wieder darauf hin, dass er nicht glaubt, dass genaue Vorhersagen gemacht werden können. Wie die meisten Menschen seiner Zeit akzeptierte Kepler das Prinzip der Astrologie, dass Himmelskörper das Geschehen auf der Erde beeinflussen können (die deutlichsten Beispiele sind die Sonne, die die Jahreszeiten und der Mond, der die Gezeiten verursacht), aber als Kopernikaner glaubte er nicht an die physikalische Realität der Sternbilder. Seine Astrologie basierte nur auf den Winkeln zwischen den Positionen der Himmelskörper („astrologische Aspekte“). Er verachtete die komplizierten Systeme der konventionellen Astrologie zutiefst.
Tod
Kepler starb nach kurzer Krankheit in Regensburg. Er hielt sich in der Stadt auf, um Geld einzutreiben, das er im Zusammenhang mit den Rudolphinischen Tafeln schuldete. Er wurde in der örtlichen Kirche begraben, die jedoch im Dreißigjährigen Krieg zerstört wurde, und von der nichts mehr übrig ist.
Historiographische Anmerkung
Manchmal wurde viel über angeblich nicht-rationale Elemente in Keplers wissenschaftlicher Tätigkeit geschrieben. Gläubige Astrologen behaupten häufig, sein Werk sei eine wissenschaftlich respektable Vorstufe zu ihrem eigenen. Der verstorbene Arthur Koestler machte in seinem einflussreichen Werk Sleepwalkers Keplers Kampf mit dem Mars zu einem Argument für die inhärente Irrationalität der modernen Wissenschaft. Es hat viele stillschweigende Anhänger dieser beiden Überzeugungen gegeben. Beide beruhen jedoch auf einer sehr unvollständigen Lektüre von Keplers Werk. Insbesondere scheint Koestler nicht die mathematischen Kenntnisse gehabt zu haben, um Keplers Verfahren zu verstehen. Eine genauere Untersuchung zeigt, dass Koestler mit seiner Einschätzung schlichtweg falsch lag.
Das wirklich wichtige nicht-rationale Element in Keplers Werk ist sein Christentum. Keplers umfangreicher und erfolgreicher Einsatz der Mathematik lässt seine Arbeit „modern“ erscheinen, aber in Wirklichkeit haben wir es mit einem christlichen Naturphilosophen zu tun, für den das Verständnis der Natur des Universums das Verständnis der Natur seines Schöpfers einschloss.