Blockchiffre-Betriebsart

Authentifizierte Verschlüsselung mit zusätzlichen Daten (AEAD) ModiBearbeiten

Eine Reihe von Betriebsmodi wurde entwickelt, um Geheimhaltung und Authentifizierung in einem einzigen kryptografischen Primitiv zu kombinieren. Beispiele für solche Modi sind Extended Cipher Block Chaining (XCBC), Integrity-Aware Cipher Block Chaining (IACBC), Integrity-Aware Parallelizable Mode (IAPM), OCB, EAX, CWC, CCM und GCM. Authentifizierte Verschlüsselungsmodi werden als Single-Pass-Modi oder Double-Pass-Modi klassifiziert. Einige Algorithmen für die authentifizierte Verschlüsselung in einem Durchgang, wie z. B. der OCB-Modus, sind durch Patente geschützt, während andere speziell entwickelt und freigegeben wurden, um eine solche Belastung zu vermeiden.

Außerdem ermöglichen einige Modi auch die Authentifizierung unverschlüsselter zugehöriger Daten, und diese werden als AEAD-Schemata (authenticated encryption with associated data) bezeichnet. Der EAX-Modus ist beispielsweise ein AEAD-Schema mit doppeltem Durchlauf, während der OCB-Modus ein einfacher Durchlauf ist.

Galois/Zähler (GCM)Bearbeiten

GCM

Galois/Zähler

Verschlüsselung parallelisierbar

Ja

Entschlüsselung parallelisierbar

Ja

Zufälliger Lesezugriff

Ja

Galois/Counter-Modus (GCM) kombiniert den bekanntenbekannte Zählermodus der Verschlüsselung mit dem neuen Galois-Modus der Authentifizierung. Das Hauptmerkmal ist die einfache parallele Berechnung der für die Authentifizierung verwendeten Galois-Feldmultiplikation. Diese Eigenschaft ermöglicht einen höheren Durchsatz als Verschlüsselungsalgorithmen.

GCM ist für Blockchiffren mit einer Blockgröße von 128 Bit definiert. Der Galois Message Authentication Code (GMAC) ist eine reine Authentifizierungsvariante des GCM, die einen inkrementellen Message Authentication Code bilden kann. Sowohl GCM als auch GMAC können Initialisierungsvektoren beliebiger Länge akzeptieren. GCM kann die Vorteile der Parallelverarbeitung voll ausschöpfen und die Implementierung von GCM kann eine Befehlspipeline oder eine Hardware-Pipeline effizient nutzen. Bei der CBC-Betriebsart kommt es zu Pipeline-Störungen, die die Effizienz und Leistung beeinträchtigen.

Wie bei CTR werden Blöcke fortlaufend nummeriert, dann wird diese Blocknummer mit einem IV kombiniert und mit einem Blockchiffre E, in der Regel AES, verschlüsselt. Das Ergebnis dieser Verschlüsselung wird dann mit dem Klartext XOR-verknüpft, um den Chiffriertext zu erhalten. Wie bei allen Zählermodi handelt es sich im Wesentlichen um eine Stromchiffre, so dass für jeden zu verschlüsselnden Strom eine andere IV verwendet werden muss.

Die Chiffretextblöcke werden als Koeffizienten eines Polynoms betrachtet, das dann an einem schlüsselabhängigen Punkt H unter Verwendung der endlichen Feldarithmetik ausgewertet wird. Das Ergebnis wird dann verschlüsselt und erzeugt ein Authentifizierungskennzeichen, mit dem die Integrität der Daten überprüft werden kann. Der verschlüsselte Text enthält dann den IV, den Chiffretext und das Authentifizierungskennzeichen.

Counter with cipher block chaining message authentication code (CCM)Bearbeiten

Counter with cipher block chaining message authentication code (counter with CBC-MAC; CCM) ist ein authentifizierter Verschlüsselungsalgorithmus, der sowohl Authentifizierung als auch Vertraulichkeit bietet. Der CCM-Modus ist nur für Blockchiffren mit einer Blocklänge von 128 Bit definiert.

Synthetischer Initialisierungsvektor (SIV)

Synthetischer Initialisierungsvektor (SIV) ist ein missbrauchsresistenter Blockchiffre-Modus.

SIV synthetisiert eine interne IV unter Verwendung einer Pseudozufallsfunktion S2V. S2V ist ein verschlüsselter Hash, der auf CMAC basiert, und die Eingabe für die Funktion ist:

• Zusätzliche authentifizierte Daten (null, ein oder mehrere AAD-Felder werden unterstützt)
• Plaintext
• Authentifizierungsschlüssel (K1).

SIV verschlüsselt die S2V-Ausgabe und den Klartext mit AES-CTR, verschlüsselt mit dem Chiffrierschlüssel (K2).

SIV kann eine externe authentifizierte Verschlüsselung auf Nonce-Basis unterstützen; in diesem Fall wird eines der authentifizierten Datenfelder für diesen Zweck verwendet. RFC5297 legt fest, dass für Interoperabilitätszwecke das letzte authentifizierte Datenfeld als externe Nonce verwendet werden sollte.

Durch die Verwendung von zwei Schlüsseln, dem Authentifizierungsschlüssel K1 und dem Verschlüsselungsschlüssel K2, können die Namensschemata für SIV-AEAD-Varianten zu einer gewissen Verwirrung führen; so bezieht sich beispielsweise AEAD_AES_SIV_CMAC_256 auf AES-SIV mit zwei AES-128-Schlüsseln und nicht auf AES-256.

AES-GCM-SIVEdit

AES-GCM-SIV ist ein Betriebsmodus für den Advanced Encryption Standard, der eine ähnliche Leistung wie der Galois/Counter-Modus sowie eine Resistenz gegen Missbrauch im Falle der Wiederverwendung einer kryptografischen Nonce bietet. Die Konstruktion ist in RFC 8452 definiert.

AES-GCM-SIV synthetisiert die interne IV. Es leitet einen Hash der zusätzlichen authentifizierten Daten und des Klartextes unter Verwendung der Galois-Hash-Funktion POLYVAL ab. Der Hash wird dann mit einem AES-Schlüssel verschlüsselt und als Authentifizierungskennzeichen und AES-CTR-Initialisierungsvektor verwendet.

AES-GCM-SIV ist eine Verbesserung gegenüber dem sehr ähnlich benannten Algorithmus GCM-SIV, mit ein paar sehr kleinen Änderungen (z.B. wie AES-CTR initialisiert wird), die aber praktische Vorteile für seine Sicherheit mit sich bringt: „Dieser Zusatz ermöglicht es, bis zu 250 Nachrichten mit demselben Schlüssel zu verschlüsseln, verglichen mit der bedeutenden Einschränkung von nur 232 Nachrichten, die mit GCM-SIV erlaubt waren.“

Confidentiality only modesEdit

Viele Betriebsmodi wurden definiert. Einige von ihnen werden im Folgenden beschrieben. Der Zweck der Chiffriermodi besteht darin, Muster zu maskieren, die in verschlüsselten Daten vorhanden sind, wie in der Beschreibung der Schwäche von ECB dargestellt.

Die verschiedenen Chiffriermodi maskieren Muster, indem sie die Ausgaben des Chiffrierblocks oder anderer global deterministischer Variablen in den nachfolgenden Chiffrierblock kaskadieren. Die Eingänge der aufgeführten Modi sind in der folgenden Tabelle zusammengefasst:

Zusammenfassung der Modi

Modus		Formeln	Ciphertext
Elektronisches Codebuch	(ECB)	Yi = F(PlainTexti, Schlüssel)	Yi
Cipher block chaining	(CBC)	Yi = PlainTexti XOR Ciphertexti-1	F(Y, Schlüssel); Ciphertext0 = IV
Propagating CBC	(PCBC)	Yi = PlainTexti XOR (Ciphertexti-1 XOR PlainTexti-1)	F(Y, Key); Ciphertext0 = IV
Cipher feedback	(CFB)	Yi = Ciphertexti-1	Plaintext XOR F(Y, Key); Ciphertext0 = IV
Ausgangsrückmeldung	(OFB)	Yi = F(Yi-1, Schlüssel); Y0 = F(IV, Key)	Plaintext XOR Yi
Zähler	(CTR)	Yi = F(IV + g(i), Key); IV = token()	Plaintext XOR Yi

Anmerkung: g(i) ist eine beliebige deterministische Funktion, oft die Identitätsfunktion.

Elektronisches Codebuch (ECB)Bearbeiten

ECB

Elektronisches Codebuch

Verschlüsselung parallelisierbar

Ja

Entschlüsselung parallelisierbar

Ja

Zufälliger Lesezugriff

Ja

Der einfachste der Verschlüsselungsmodi ist der Modus des elektronischen Codebuchs (ECB) (benannt nach den herkömmlichen physischen Codebüchern). Die Nachricht wird in Blöcke unterteilt, und jeder Block wird separat verschlüsselt.

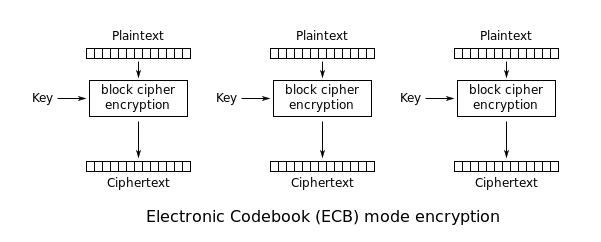
Der Nachteil dieser Methode ist die mangelnde Verbreitung. Da ECB identische Klartextblöcke in identische Chiffretextblöcke verschlüsselt, lassen sich Datenmuster nicht gut verbergen. ECB wird für die Verwendung in kryptografischen Protokollen nicht empfohlen.

Ein anschauliches Beispiel für das Ausmaß, in dem ECB Klartextdatenmuster im Chiffretext zurücklassen kann, ist zu sehen, wenn der ECB-Modus zur Verschlüsselung eines Bitmap-Bildes verwendet wird, das große Bereiche mit einheitlicher Farbe verwendet. Während die Farbe jedes einzelnen Pixels verschlüsselt wird, kann das Gesamtbild immer noch erkannt werden, da das Muster der identisch gefärbten Pixel im Original in der verschlüsselten Version erhalten bleibt.

Der EZB-Modus kann auch Protokolle ohne Integritätsschutz noch anfälliger für Wiederholungsangriffe machen, da jeder Block auf genau dieselbe Weise entschlüsselt wird.

Cipher block chaining (CBC)Bearbeiten

CBC

Cipher block chaining

Verschlüsselung parallelisierbar

Nein

Entschlüsselung parallelisierbar

Ja

Zufälliger Lesezugriff

Ja

Ehrsam, Meyer, Smith und Tuchman erfanden 1976 die Cipher Block Chaining (CBC) Betriebsart. Im CBC-Modus wird jeder Klartextblock vor der Verschlüsselung mit dem vorherigen Chiffretextblock XOR-verknüpft. Auf diese Weise hängt jeder Chiffriertextblock von allen bis dahin verarbeiteten Klartextblöcken ab. Um jede Nachricht eindeutig zu machen, muss im ersten Block ein Initialisierungsvektor verwendet werden.

Wenn der erste Block den Index 1 hat, lautet die mathematische Formel für die CBC-Verschlüsselung

C i = E K ( P i ⊕ C i – 1 ) , {\displaystyle C_{i}=E_{K}(P_{i}\oplus C_{i-1}),}

C 0 = I V , {\displaystyle C_{0}=IV,}

während die mathematische Formel für CBC-Entschlüsselung lautet

P i = D K ( C i ) ⊕ C i – 1 , {\displaystyle P_{i}=D_{K}(C_{i})\oplus C_{i-1},}

C 0 = I V . {C_{0}=IV.}

BeispielBearbeiten

CBC ist die am häufigsten verwendete Betriebsart. Seine Hauptnachteile sind, dass die Verschlüsselung sequentiell ist (d.h. sie kann nicht parallelisiert werden) und dass die Nachricht auf ein Vielfaches der Chiffrierblockgröße aufgefüllt werden muss. Eine Möglichkeit, das letzte Problem zu lösen, ist das so genannte Ciphertext Stealing. Beachten Sie, dass eine Ein-Bit-Änderung in einem Klartext- oder Initialisierungsvektor (IV) alle nachfolgenden Chiffretextblöcke beeinflusst.

Die Entschlüsselung mit dem falschen IV führt dazu, dass der erste Klartextblock beschädigt wird, die nachfolgenden Klartextblöcke jedoch korrekt sind. Das liegt daran, dass jeder Block mit dem Chiffriertext des vorherigen Blocks XOR-verknüpft wird, nicht mit dem Klartext, so dass man den vorherigen Block nicht entschlüsseln muss, bevor man ihn als IV für die Entschlüsselung des aktuellen Blocks verwendet. Dies bedeutet, dass ein Klartextblock aus zwei benachbarten Blöcken des Geheimtextes wiederhergestellt werden kann. Infolgedessen kann die Entschlüsselung parallelisiert werden. Es ist zu beachten, dass eine Änderung des Chiffriertextes um ein Bit zu einer vollständigen Verfälschung des entsprechenden Klartextblocks führt und das entsprechende Bit im folgenden Klartextblock invertiert, während die übrigen Blöcke intakt bleiben. Diese Besonderheit wird bei verschiedenen Padding-Orakel-Angriffen wie POODLE ausgenutzt.

Explizite Initialisierungsvektoren machen sich diese Eigenschaft zunutze, indem sie dem Klartext einen einzelnen Zufallsblock voranstellen. Die Verschlüsselung erfolgt wie üblich, mit der Ausnahme, dass die IV der Entschlüsselungsroutine nicht mitgeteilt werden muss. Unabhängig davon, welcher IV bei der Entschlüsselung verwendet wird, ist nur der Zufallsblock „beschädigt“. Er kann sicher verworfen werden, und der Rest der Entschlüsselung ist der ursprüngliche Klartext.

Propagating cipher block chaining (PCBC)Bearbeiten

PCBC

Propagating cipher block chaining

Verschlüsselung parallelisierbar

Nein

Entschlüsselung parallelisierbar

Nein

Zufälliger Lesezugriff

Nein

Der Modus Propagating Cipher Block Chaining oder Klartext Chipher-Blockverkettungsmodus wurde entwickelt, um kleine Änderungen im Chiffretext bei der Entschlüsselung unbegrenzt weiterzugeben, als auch beim Verschlüsseln. Im PCBC-Modus wird jeder Klartextblock vor der Verschlüsselung sowohl mit dem vorherigen Klartextblock als auch mit dem vorherigen Chiffretextblock XOR-verknüpft. Wie beim CBC-Modus wird im ersten Block ein Initialisierungsvektor verwendet.

Die Verschlüsselungs- und Entschlüsselungsalgorithmen sind wie folgt:

C i = E K ( P i ⊕ P i – 1 ⊕ C i – 1 ) , P 0 ⊕ C 0 = I V , {\displaystyle C_{i}=E_{K}(P_{i}\oplus P_{i-1}\oplus C_{i-1}),P_{0}\oplus C_{0}=IV,}

P i = D K ( C i ) ⊕ P i – 1 ⊕ C i – 1 , P 0 ⊕ C 0 = I V . {\displaystyle P_{i}=D_{K}(C_{i})\oplus P_{i-1}\oplus C_{i-1},P_{0}\oplus C_{0}=IV.}

PCBC wird vor allem in Kerberos v4 und WASTE verwendet, ist aber ansonsten nicht üblich. Wenn bei einer im PCBC-Modus verschlüsselten Nachricht zwei benachbarte Chiffretextblöcke ausgetauscht werden, hat dies keinen Einfluss auf die Entschlüsselung der nachfolgenden Blöcke. Aus diesem Grund wird PCBC in Kerberos v5 nicht verwendet.

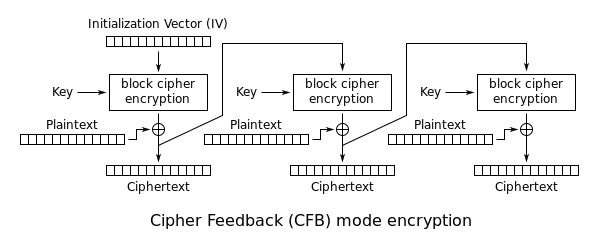
Chiffrierrückmeldung (CFB)Bearbeiten

Voll-block CFBEdit

CFB

Cipher feedback

Verschlüsselung parallelisierbar

Nein

Entschlüsselung parallelisierbar

Ja

Zufälliger Lesezugriff

Ja

Der Cipher Feedback (CFB) Modus, In seiner einfachsten Form wird die gesamte Ausgabe der Blockchiffre verwendet. In dieser Variante, die der CBC sehr ähnlich ist, wird aus einer Blockchiffre eine selbstsynchronisierende Stromchiffre. Die CFB-Entschlüsselung in dieser Variante ist fast identisch mit der CBC-Verschlüsselung in umgekehrter Form:

C i = { IV , i = 0 E K ( C i – 1 ) ⊕ P i , sonst P i = E K ( C i – 1 ) ⊕ C i , {\displaystyle {\begin{aligned}C_{i}&={\begin{cases}{\text{IV}},&i=0\\E_{K}(C_{i-1})\oplus P_{i},&{\text{otherwise}}\end{cases}}\\P_{i}&=E_{K}(C_{i-1})\oplus C_{i},\end{aligned}}}

CFB-1, CFB-8, CFB-64, CFB-128, usw.Bearbeiten

NIST SP800-38A definiert CFB mit einer Bitbreite. Der CFB-Modus erfordert auch einen ganzzahligen Parameter, bezeichnet mit s, so dass 1 ≤ s ≤ b. In der nachstehenden Spezifikation des CFB-Modus besteht jedes Klartextsegment (Pj) und jedes Chiffretextsegment (Cj) aus s Bits. Der Wert von s wird manchmal in den Namen des Modus aufgenommen, z. B. der 1-Bit-CFB-Modus, der 8-Bit-CFB-Modus, der 64-Bit-CFB-Modus oder der 128-Bit-CFB-Modus.

Diese Modi kürzen die Ausgabe der zugrunde liegenden Blockchiffre ab.

I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}

I i = ( ( I i – 1 ≪ s ) + C i ) mod 2 b , {\displaystyle I_{i}={\big (}(I_{i-1}\ll s)+C_{i}{\big )}{\bmod {2}}^{b},}

C i = MSB s ( E K ( I i – 1 ) ) ⊕ P i , {\displaystyle C_{i}=\operatorname {MSB} _{s}{\big (}E_{K}(I_{i-1}){\big )}\oplus P_{i},}

P i = MSB s ( E K ( I i – 1 ) ) ⊕ C i , {\displaystyle P_{i}=\operatorname {MSB} (}E_{K}(I_{i-1}){\big )}\oplus C_{i},}

CFB-1 gilt als selbstsynchronisierend und widerstandsfähig gegen den Verlust von Chiffretext; „Wenn der 1-Bit-CFB-Modus verwendet wird, dann wird die Synchronisation automatisch b+1 Positionen nach dem eingefügten oder gelöschten Bit wiederhergestellt. Für andere Werte von s im CFB-Modus und für die anderen Vertraulichkeitsmodi in dieser Empfehlung muss die Synchronisation extern wiederhergestellt werden.“ (NIST SP800-38A). D.h. ein 1-Bit-Verlust in einer 128-Bit-breiten Blockchiffre wie AES macht 129 Bits ungültig, bevor gültige Bits ausgegeben werden.

CFB kann sich auch in einigen anderen als den angegebenen Sonderfällen selbst synchronisieren. Zum Beispiel wird eine Ein-Bit-Änderung in CFB-128 mit einer zugrundeliegenden 128-Bit-Blockchiffre nach zwei Blöcken neu synchronisiert. (CFB-128 usw. kann jedoch nicht mit Bitverlusten umgehen; ein Ein-Bit-Verlust führt dazu, dass der Entschlüsseler die Ausrichtung mit dem Verschlüsseler verliert)

CFB im Vergleich zu anderen ModiBearbeiten

Wie im CBC-Modus werden Änderungen im Klartext für immer in den Geheimtext übertragen, und die Verschlüsselung kann nicht parallelisiert werden. Wie bei CBC kann auch die Entschlüsselung parallelisiert werden.

CFB, OFB und CTR haben zwei Vorteile gegenüber dem CBC-Modus: Die Blockchiffre wird immer nur in der Verschlüsselungsrichtung verwendet, und die Nachricht muss nicht auf ein Vielfaches der Chiffrierblockgröße aufgefüllt werden (obwohl Ciphertext-Stealing auch für den CBC-Modus verwendet werden kann, um das Auffüllen unnötig zu machen).

Output-Feedback (OFB)Bearbeiten

OFB

Output-Feedback

Verschlüsselung parallelisierbar

Nein

Entschlüsselung Parallelisierbar

Nein

Zufälliger Lesezugriff

Nein

Der Modus „Output Feedback“ (OFB) macht aus einer Blockchiffre eine synchrone Stromchiffre. Sie erzeugt Schlüsselstromblöcke, die dann mit den Klartextblöcken XOR-verknüpft werden, um den Chiffretext zu erhalten. Genau wie bei anderen Stromchiffren führt das Umdrehen eines Bits im Chiffretext zu einem umgedrehten Bit im Klartext an derselben Stelle. Dank dieser Eigenschaft können viele Fehlerkorrekturcodes auch dann normal funktionieren, wenn sie vor der Verschlüsselung angewendet werden.

Aufgrund der Symmetrie der XOR-Operation sind Verschlüsselung und Entschlüsselung genau gleich:

C j = P j ⊕ O j , {\displaystyle C_{j}=P_{j}\oplus O_{j},}

P j = C j ⊕ O j , {\displaystyle P_{j}=C_{j}\oplus O_{j},}

O j = E K ( I j ) , {\displaystyle O_{j}=E_{K}(I_{j}),}

I j = O j – 1 , {\displaystyle I_{j}=O_{j-1},}

I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}

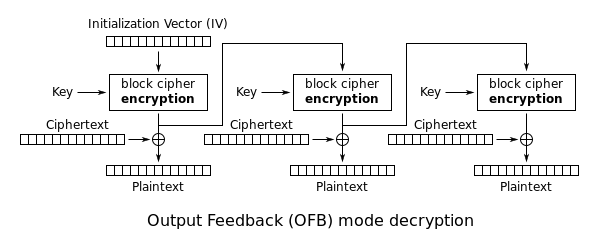
Jede Output-Feedback-Blockchiffrieroperation hängt von allen vorhergehenden ab und kann daher nicht parallel durchgeführt werden. Da der Klartext oder Chiffretext jedoch nur für die abschließende XOR-Operation verwendet wird, können die Blockchiffrieroperationen im Voraus durchgeführt werden, so dass der abschließende Schritt parallel durchgeführt werden kann, sobald der Klartext oder Chiffretext verfügbar ist.

Es ist möglich, einen OFB-Schlüsselstrom zu erhalten, indem der CBC-Modus mit einer konstanten Folge von Nullen als Eingabe verwendet wird. Dies kann nützlich sein, weil es die Verwendung von schnellen Hardware-Implementierungen des CBC-Modus für die OFB-Modus-Verschlüsselung ermöglicht.

Die Verwendung des OFB-Modus mit einem Teilblock als Rückmeldung wie beim CFB-Modus reduziert die durchschnittliche Zykluslänge um einen Faktor von 232 oder mehr. Ein von Davies und Parkin vorgeschlagenes und durch experimentelle Ergebnisse untermauertes mathematisches Modell hat gezeigt, dass nur bei vollständiger Rückkopplung eine durchschnittliche Zykluslänge nahe dem erreichbaren Maximum erzielt werden kann. Aus diesem Grund wurde die Unterstützung für eine verkürzte Rückkopplung aus der Spezifikation von OFB entfernt.

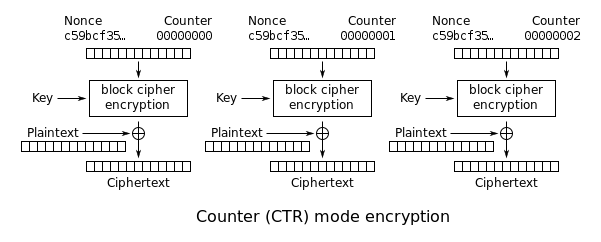
Zähler (CTR)Bearbeiten

CTR

Zähler

Verschlüsselung parallelisierbar

Ja

Entschlüsselung parallelisierbar

Ja

Zufälliger Lesezugriff

Ja

Anmerkung: Der CTR-Modus (CM) wird auch als Integer-Zähler-Modus (ICM) und segmentierter Integer-Zähler-Modus (SIC) bezeichnet.

Wie OFB verwandelt der Zählermodus eine Blockchiffre in eine Stromchiffre. Er erzeugt den nächsten Schlüsselstromblock durch Verschlüsselung aufeinander folgender Werte eines „Zählers“. Bei dem Zähler kann es sich um eine beliebige Funktion handeln, die eine Sequenz erzeugt, die sich garantiert über einen langen Zeitraum nicht wiederholt, wobei ein Zähler, der um eins erhöht wird, am einfachsten und beliebtesten ist. Die Verwendung einer einfachen deterministischen Eingabefunktion war früher umstritten; Kritiker argumentierten, dass „ein Kryptosystem absichtlich einer bekannten systematischen Eingabe ausgesetzt wird, was ein unnötiges Risiko darstellt“. Heutzutage ist der CTR-Modus jedoch weithin akzeptiert, und jegliche Probleme werden als Schwäche der zugrunde liegenden Blockchiffre betrachtet, von der man erwartet, dass sie unabhängig von systematischen Verzerrungen in ihrer Eingabe sicher ist. Der CTR-Modus ist neben dem CBC-Modus einer der beiden von Niels Ferguson und Bruce Schneier empfohlenen Blockchiffriermodi.

Der CTR-Modus wurde 1979 von Whitfield Diffie und Martin Hellman eingeführt.

Der CTR-Modus hat ähnliche Eigenschaften wie OFB, ermöglicht aber zusätzlich einen zufälligen Zugriff während der Entschlüsselung. Der CTR-Modus eignet sich gut für den Betrieb auf einer Multiprozessormaschine, auf der Blöcke parallel verschlüsselt werden können. Wenn die IV/Nonce zufällig ist, können sie zusammen mit dem Zähler durch eine beliebige invertierbare Operation (Verkettung, Addition oder XOR) kombiniert werden, um den eigentlichen eindeutigen Zählerblock für die Verschlüsselung zu erzeugen. Im Falle einer nicht zufälligen Nonce (z. B. eines Paketzählers) sollten Nonce und Zähler verkettet werden (z. B. Speicherung der Nonce in den oberen 64 Bit und des Zählers in den unteren 64 Bit eines 128-Bit-Zählerblocks). Eine einfache Addition oder XOR-Verknüpfung von Nonce und Zähler zu einem einzigen Wert würde in vielen Fällen die Sicherheit bei einem „chosen-plaintext“-Angriff aufheben, da der Angreifer in der Lage sein könnte, das gesamte IV-Zähler-Paar zu manipulieren, um eine Kollision zu verursachen. Sobald ein Angreifer das IV-Zähler-Paar und den Klartext kontrolliert, würde die XOR-Verknüpfung des Chiffriertextes mit dem bekannten Klartext einen Wert ergeben, der bei XOR-Verknüpfung mit dem Chiffriertext des anderen Blocks, der sich das gleiche IV-Zähler-Paar teilt, diesen Block entschlüsseln würde.

Beachten Sie, dass die Nonce in diesem Diagramm dem Initialisierungsvektor (IV) in den anderen Diagrammen entspricht. Wenn jedoch die Offset-/Standortinformationen beschädigt sind, ist es aufgrund der Abhängigkeit vom Byte-Offset unmöglich, diese Daten teilweise wiederherzustellen.