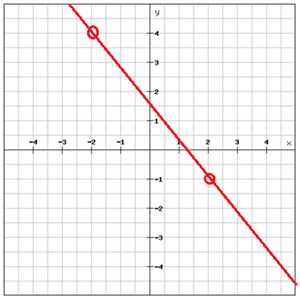
En ligning i hældningsintervalformen skrives som
$$$y=mx+b$$
Hvor m er linjens hældning og b er y-intervallet. Du kan bruge denne ligning til at skrive en ligning, hvis du kender hældningen og y-interceptet.
Eksempel
Find ligningen for linjen
Vælg to punkter, der ligger på linjen
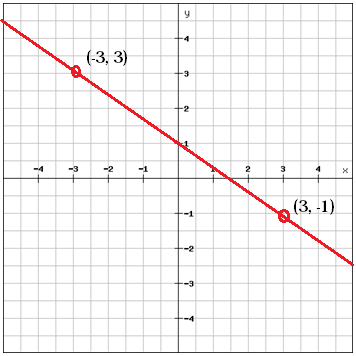
Beregn hældningen mellem de to punkter
$$$m=\frac{y_{2}\, -y_{1}}{x_{2}\, -x_{1}}}=\frac{\left (-1 \right )-3}{3-\left ( -3 \right )}=\frac{-4}{6}=\frac{-2}{3}$$$
Vi kan finde b-værdien, y-interceptet, ved at se på grafen
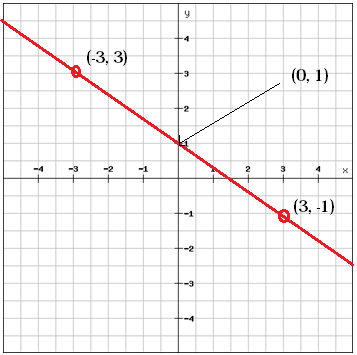
b = 1
Vi har fået en værdi for m og en værdi for b. Dette giver os den lineære funktion
$$$y=-\frac{2}{3}x+1$$$
I mange tilfælde er værdien af b ikke så let at aflæse. I disse tilfælde, eller hvis du er usikker på, om linjen rent faktisk krydser y-aksen i netop dette punkt, kan du beregne b ved at løse ligningen for b og derefter erstatte x og y med et af dine to punkter.
Vi kan bruge eksemplet ovenfor til at illustrere dette. Vi har de to punkter (-3, 3) og (3, -1). Ud fra disse to punkter har vi beregnet hældningen
$$$m=-\frac{2}{3}$$$
Dette giver os ligningen
$$y=-\frac{2}{3}x+b$$$
Derfra kan vi løse ligningen for b
$$b=y+\frac{2}{3}x$$$
Og hvis vi sætter værdierne fra vores første punkt ind (-3, 3) får vi
$$$b=3+\frac{2}{3}\cdot \left ( -3 \right )=3+\left ( -2 \right )=1$$$
Hvis vi indsætter denne værdi for b i ligningen, får vi
$$y=-\frac{2}{3}x+1$$$
hvilket er den samme ligning, som vi fik, da vi aflæste y-interceptet fra grafen.
For at opsummere, hvordan man skriver en lineær ligning ved hjælp af hældningsinterceptionsformen skal man
- Identificere hældningen, m. Dette kan gøres ved at beregne hældningen mellem to kendte punkter på linjen ved hjælp af hældningsformlen.
- Find y-interceptet. Dette kan gøres ved at indsætte hældningen og koordinaterne for et punkt (x, y) på linjen i hældningsinterceptformlen og derefter løse for b.
Når du har fået både m og b, kan du bare sætte dem ind i ligningen på deres respektive position.
Videolektion
Find ligningen til grafen