Selection Sort – Algoritme, kildekode, tidskompleksitet

Denne artikel er en del af serien “Sorteringsalgoritmer”: Ultimate Guide” og …

• beskriver, hvordan Selection Sort fungerer,
• indbefatter Java-kildekoden til Selection Sort,
• viser, hvordan man udleder dens tidskompleksitet (uden kompliceret matematik)
• og kontrollerer, om Java-implementeringens ydeevne passer til den forventede køretidsadfærd.

Du kan finde kildekoden til hele artikelserien i mit GitHub-repository.

Eksempel: Sortering af spillekort

Sortering af spillekort på hånden er det klassiske eksempel på Insertion Sort.

Selection Sort kan også illustreres med spillekort. Jeg kender ikke nogen, der samler deres kort op på denne måde, men som eksempel fungerer det ganske godt 😉

Først lægger du alle dine kort med billedsiden opad på bordet foran dig. Du leder efter det mindste kort og tager det til venstre for din hånd. Derefter leder du efter det næste større kort og lægger det til højre for det mindste kort og så videre, indtil du til sidst tager det største kort yderst til højre.

forskel til Indsætningssortering

Med Indsætningssortering tog vi det næste usorterede kort og satte det ind på den rigtige plads i de sorterede kort.

Selektionssortering fungerer lidt omvendt: Vi vælger det mindste kort blandt de usorterede kort og føjer det så – den ene efter den anden – til de allerede sorterede kort.

Selektionssorteringsalgoritme

Algoritmen kan forklares mest enkelt med et eksempel. I de følgende trin viser jeg, hvordan man sorterer arrayet med Selection Sort:

Stræk 1

Vi opdeler arrayet i en venstre, sorteret del og en højre, usorteret del. Den sorterede del er tom i begyndelsen:

Strin 2

Vi søger efter det mindste element i den højre, usorterede del. For at gøre dette husker vi først det første element, som er 6. Vi går til det næste felt, hvor vi finder et endnu mindre element i 2. Vi går over resten af arrayet, hvor vi leder efter et endnu mindre element. Da vi ikke kan finde et, holder vi os til 2. Vi sætter det på den rigtige plads ved at bytte det med elementet på første plads. Derefter flytter vi grænsen mellem arrayafsnittene et felt til højre:

Stræk 3

Vi søger igen i den højre, usorterede del efter det mindste element. Denne gang er det 3’eren; vi bytter den med elementet i anden position:

Stræk 4

Vi søger igen efter det mindste element i den højre del. Det er 4, som allerede befinder sig i den rigtige position. Så der er ikke behov for en bytteoperation i dette trin, og vi flytter blot sektionsgrænsen:

Strg 5

Som det mindste element finder vi 6’eren. Vi bytter det med elementet i begyndelsen af den højre del, 9:

Stræk 6

Af de resterende to elementer er 7 det mindste. Vi bytter det med 9’eren:

Algoritme afsluttet

Det sidste element er automatisk det største og derfor i den rigtige position. Algoritmen er færdig, og elementerne er sorteret:

Selection Sort Java Source Code

I dette afsnit finder du en simpel Java-implementering af Selection Sort.

Den ydre løkke itererererer over de elementer, der skal sorteres, og den slutter efter det næstsidste element. Når dette element er sorteret, bliver det sidste element også automatisk sorteret. Sløjfevariablen i peger altid på det første element i den højre, usorterede del.

I hver sløjfecyklus antages det første element i den højre del indledningsvis at være det mindste element min; dets position gemmes i minPos.

Den indre løkke itererer derefter fra det andet element i den højre del til dens ende og omfordeler min og minPos, hver gang der findes et endnu mindre element.

Når den indre løkke er afsluttet, byttes elementerne på positionerne i (begyndelsen af den højre del) og minPos om (medmindre de er det samme element).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

Den viste kode adskiller sig fra SelectionSort-klassen i GitHub-repositoriet, idet den implementerer grænsefladen SortAlgorithm for let at kunne udskiftes inden for testrammen.

Selection Sort Time Complexity

Vi betegner med n antallet af elementer, i vores eksempel n = 6.

De to indlejrede sløjfer er en indikation af, at vi har at gøre med en tidskompleksitet* på O(n²). Dette vil være tilfældet, hvis begge sløjfer itererer til en værdi, der stiger lineært med n.

Det er naturligvis tilfældet med den yderste sløjfe: den tæller op til n-1.

Hvad med den indre sløjfe?

Se på følgende illustration:

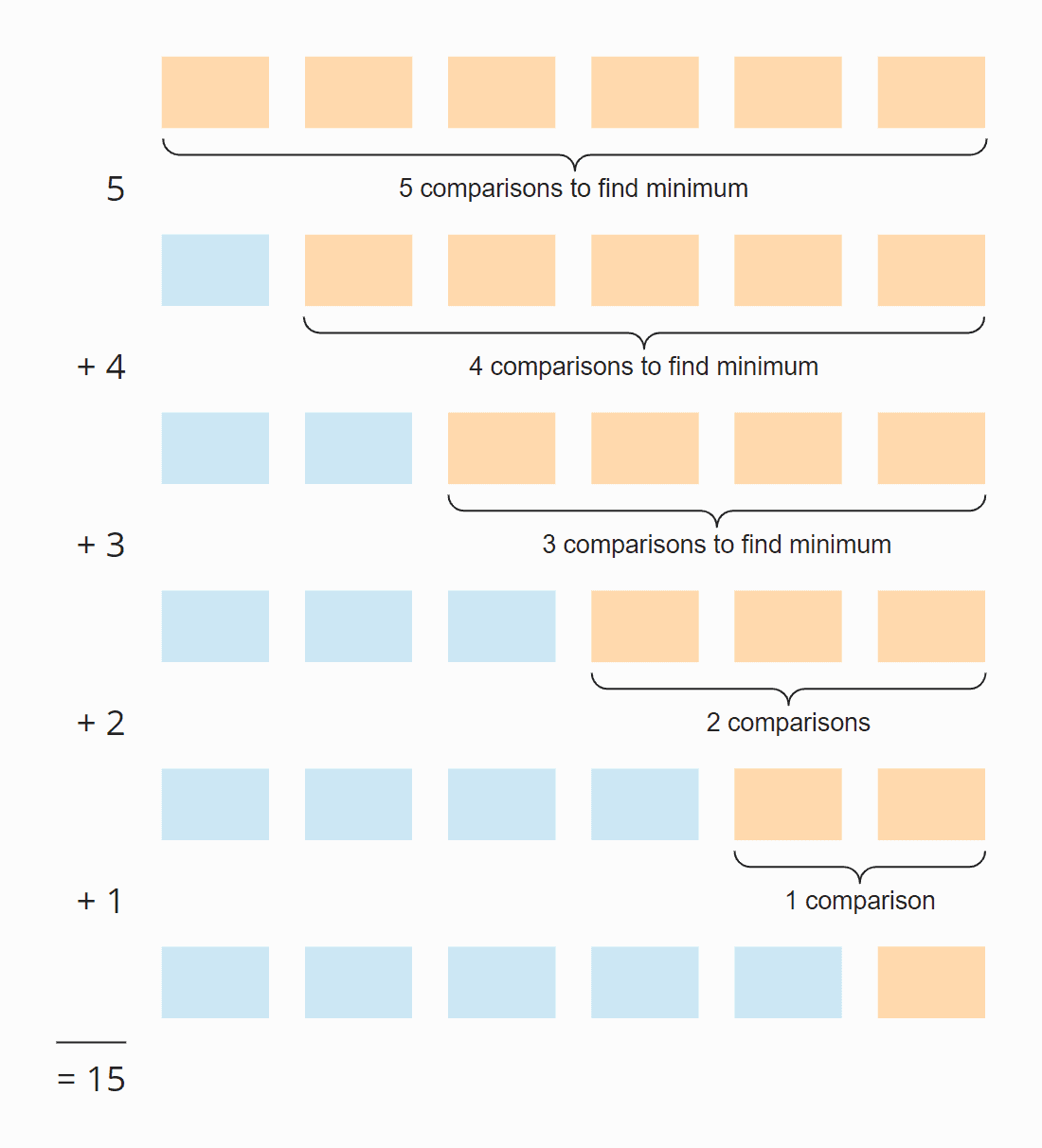
I hvert trin er antallet af sammenligninger én mindre end antallet af usorterede elementer. I alt er der 15 sammenligninger – uanset om arrayet oprindeligt er sorteret eller ej.

Dette kan også beregnes på følgende måde:

Seks elementer gange fem trin; divideret med to, da halvdelen af elementerne i gennemsnit over alle trin stadig er usorterede:

6 × 5 × 5 × ½ = 30 × ½ = 15

Hvis vi erstatter 6 med n, får vi

n × (n – 1) × ½

Ved multiplikation er det:

½ n² – ½ n

Den højeste potens af n i dette udtryk er n². Tidskompleksiteten for at søge efter det mindste element er derfor O(n²) – også kaldet “kvadratisk tid”.

Lad os nu se på ombytningen af elementerne. I hvert trin (undtagen det sidste) byttes enten et element eller intet element, alt efter om det mindste element allerede befinder sig på den korrekte position eller ej. Vi har således i alt maksimalt n-1 swapping-operationer, dvs. en tidskompleksitet på O(n) – også kaldet “lineær tid”.

For den samlede kompleksitet betyder kun den højeste kompleksitetsklasse noget, derfor:

Den gennemsnitlige, best-case og worst-case tidskompleksitet for Selection Sort er:

Den gennemsnitlige, best-case og worst-case tidskompleksitet for Selection Sort er: O(n²)

* Begreberne “tidskompleksitet” og “O-notation” forklares i denne artikel ved hjælp af eksempler og diagrammer.

Løbetid for Java Selection Sort Eksempel

Godt nok teori! Jeg har skrevet et testprogram, der måler løbetiden for Selection Sort (og alle andre sorteringsalgoritmer, der er behandlet i denne serie) på følgende måde:

• Antallet af elementer, der skal sorteres, fordobles efter hver iteration fra oprindeligt 1.024 elementer op til 536.870.912 (= 229) elementer. Et array af dobbelt så stor størrelse kan ikke oprettes i Java.
• Hvis en test tager mere end 20 sekunder, udvides arrayet ikke yderligere.
• Alle tests køres med usorterede samt op- og nedstigende forsorterede elementer.
• Vi lader HotSpot-compileren optimere koden med to opvarmningsrunder. Herefter gentages testene, indtil processen afbrydes.

Efter hver iteration udskriver programmet medianen af alle tidligere måleresultater.

Her er resultatet for Selection Sort efter 50 iterationer (for overskuelighedens skyld er dette kun et uddrag; det fuldstændige resultat kan findes her):

n	sorteret	opstigende	nedstigende	nedstigende
…	…	…	…
16,384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Her er målingerne endnu en gang som et diagram (hvor jeg har vist “usorteret” og “stigende” som én kurve på grund af de næsten identiske værdier):

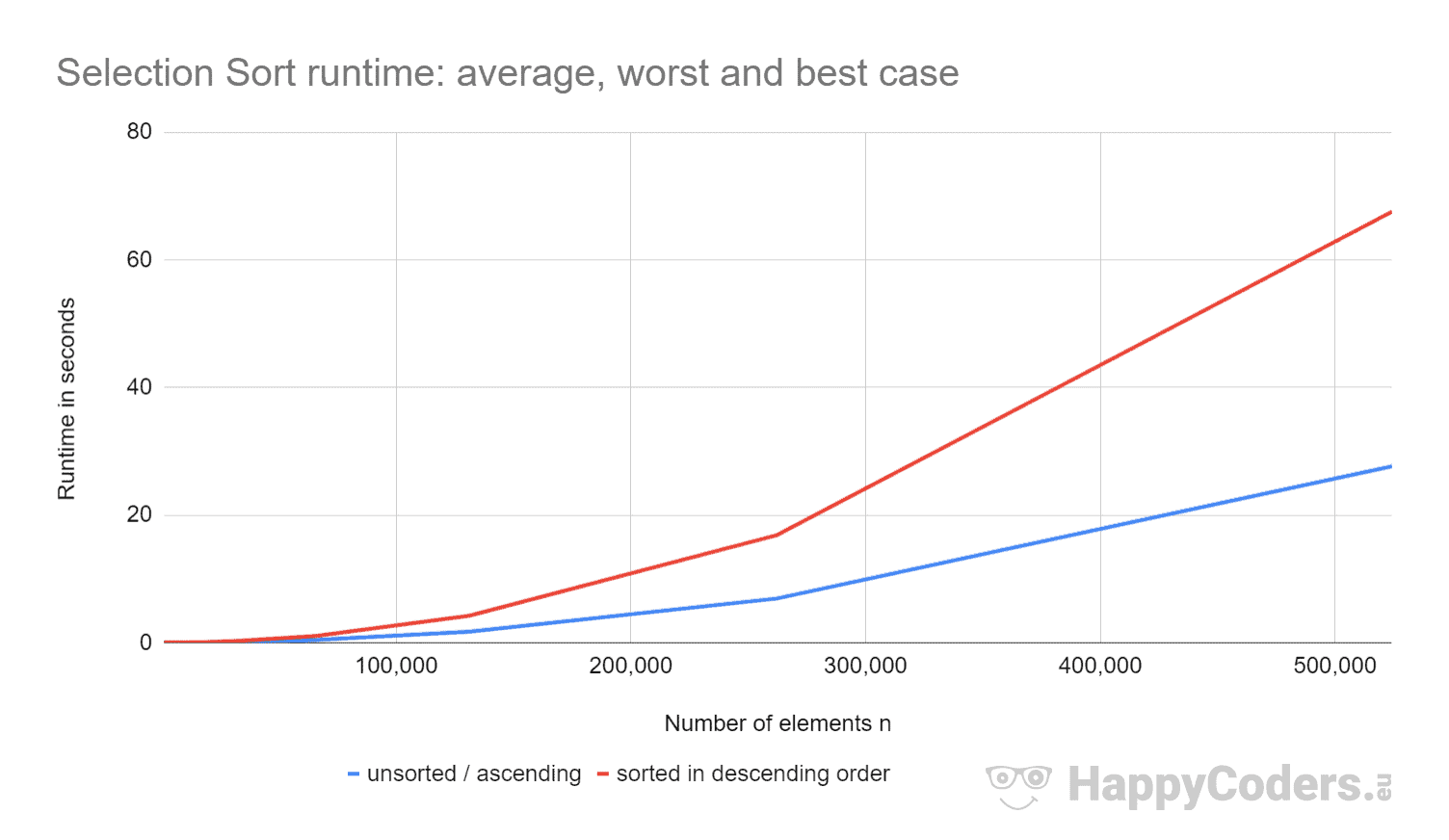
Det er godt at se, at

• hvis antallet af elementer fordobles, bliver løbetiden ca. firedoblet – uanset om elementerne i forvejen er sorteret eller ej. Dette svarer til den forventede tidskompleksitet O(n²).
• at køretiden for opstigende sorterede elementer er en smule bedre end for usorterede elementer. Dette skyldes, at swapping-operationerne, der – som analyseret ovenfor – er af ringe betydning, ikke er nødvendige her.
• at løbetiden for nedadgående sorterede elementer er betydeligt dårligere end for usorterede elementer.

Hvorfor det?

Analyse af den værst tænkelige løbetid

Theoretisk set burde søgningen efter det mindste element altid tage lige lang tid, uanset udgangssituationen. Og bytteoperationerne burde kun være lidt mere for elementer sorteret i faldende rækkefølge (for elementer sorteret i faldende rækkefølge skal hvert element byttes; for usorterede elementer skal næsten hvert element byttes).

Ved hjælp af programmet CountOperations fra mit GitHub-repository kan vi se antallet af forskellige operationer. Her er resultaterne for usorterede elementer og elementer sorteret i faldende rækkefølge, opsummeret i én tabel:

n	Sammenligninger	Swaps usorteret	Swaps nedadgående	minPos/min usorteret	minPos/min nedadgående
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

Fra de målte værdier kan ses:

• Med elementer sorteret i faldende rækkefølge har vi – som forventet – lige så mange sammenligningsoperationer som med usorterede elementer – dvs. n × (n-1)/2.
• Med usorterede elementer har vi – som antaget – næsten lige så mange bytteoperationer som elementer: f.eks. er der med 4.096 usorterede elementer 4.084 bytteoperationer. Disse tal ændrer sig tilfældigt fra test til test.
• Men med elementer sorteret i faldende rækkefølge har vi kun halvt så mange swap-operationer som elementer! Det skyldes, at vi, når vi bytter, ikke kun placerer det mindste element på den rigtige plads, men også den respektive byttepartner.

Med otte elementer har vi f.eks. fire bytteoperationer. I de første fire iterationer har vi én hver, og i iterationerne fem til otte ingen (ikke desto mindre kører algoritmen videre til slutningen):

Vi kan desuden aflæse af målingerne:

• Grunden til, at Selection Sort er så meget langsommere med elementer sorteret i faldende rækkefølge, kan findes i antallet af lokale variabeltildelinger (minPos og min), når vi søger efter det mindste element. Mens vi med 8 192 usorterede elementer har 69 378 af disse tildelinger, er der med elementer sorteret i aftagende rækkefølge 16 785 407 sådanne tildelinger – det er 242 gange så mange!

Hvorfor denne enorme forskel?

Analyse af løbetiden for søgning efter det mindste element

For elementer sorteret i aftagende rækkefølge kan størrelsesordenen udledes af illustrationen lige ovenfor. Søgningen efter det mindste element er begrænset til trekanten af de orange og orange-blå kasser. I den øverste orange del bliver tallene i hver kasse mindre; i den højre orange-blå del stiger tallene igen.

Tildelingsoperationer finder sted i hver orange boks og i den første af de orange-blå bokse. Antallet af tildelingsoperationer for minPos og min er således billedligt talt ca. “en fjerdedel af kvadratet” – matematisk og præcist er det ¼ n² + n – 1.

For usorterede elementer skulle vi trænge meget dybere ind i sagen. Det ville ikke blot gå ud over rammerne for denne artikel, men for hele bloggen.

Derfor begrænser jeg min analyse til et lille demoprogram, der måler, hvor mange minPos/min-tildelinger der er, når man søger efter det mindste element i et usorteret array. Her er gennemsnitsværdierne efter 100 iterationer (et lille uddrag; de komplette resultater kan findes her):

n	gennemsnitligt antal minPos/min-opgaver
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Her som et diagram med logaritmisk x-akse:

Diagrammet viser meget fint, at vi har logaritmisk vækst, dvs, med hver fordobling af antallet af elementer stiger antallet af opgaver kun med en konstant værdi. Som sagt vil jeg ikke gå dybere ind i matematiske baggrunde.

Det er grunden til, at disse minPos/min-tildelinger er af ringe betydning i usorterede arrays.

Andre karakteristika ved Selection Sort

I de følgende afsnit vil jeg diskutere rumkompleksiteten, stabiliteten og paralleliserbarheden ved Selection Sort.

Rumkompleksitet af Selection Sort

Selection Sorts rumkompleksitet er konstant, da vi ikke har brug for yderligere hukommelsesplads ud over løkkevariablerne i og j og hjælpevariablerne length, minPos og min.

Det vil sige, at uanset hvor mange elementer vi sorterer – ti eller ti millioner – har vi altid kun brug for disse fem ekstra variabler. Vi noterer konstant tid som O(1).

Stabilitet af selektionssortering

Selektionssortering synes ved første øjekast stabil: Hvis den usorterede del indeholder flere elementer med samme nøgle, skal det første element først føjes til den sorterede del.

Men udseendet er bedragerisk. For ved at bytte om på to elementer i algoritmens andet undertrin kan det ske, at visse elementer i den usorterede del ikke længere har den oprindelige rækkefølge. Dette fører igen til, at de ikke længere optræder i den oprindelige rækkefølge i den sorterede del.

Et eksempel kan konstrueres meget enkelt. Lad os antage, at vi har to forskellige elementer med nøgle 2 og et med nøgle 1, der er arrangeret som følger, og derefter sorterer dem med Selection Sort:

I det første trin byttes det første og det sidste element om. Således ender elementet “TWO” bag elementet “two” – rækkefølgen af begge elementer er byttet om.

I det andet trin sammenligner algoritmen de to bageste elementer. Begge har den samme nøgle, 2. Der byttes altså ikke noget element.

I det tredje trin er der kun ét element tilbage; dette betragtes automatisk som sorteret.

De to elementer med nøglen 2 er således blevet byttet til deres oprindelige rækkefølge – algoritmen er ustabil.

Stabil variant af Selection Sort

Selection Sort kan gøres stabil ved ikke at bytte det mindste element med det første i trin to, men ved at flytte alle elementer mellem det første og det mindste element en position til højre og indsætte det mindste element i begyndelsen.

Selv om tidskompleksiteten forbliver den samme som følge af denne ændring, vil de ekstra forskydninger føre til en betydelig ydelsesforringelse, i det mindste når vi sorterer et array.

Med en linket liste vil klipning og indsættelse af det element, der skal sorteres, kunne ske uden væsentlige ydelsestab.

Paralleliserbarhed af selektionssortering

Vi kan ikke parallelisere den ydre løkke, fordi den ændrer indholdet af arrayet i hver iteration.

Den indre sløjfe (søgning efter det mindste element) kan paralleliseres ved at opdele arrayet, søge efter det mindste element i hvert delarray parallelt og sammenlægge de mellemliggende resultater.

Selection Sort vs. Insertion Sort

Hvilken algoritme er hurtigere, Selection Sort eller Insertion Sort?

Lad os sammenligne målingerne fra mine Java-implementeringer.

Jeg udelader det bedste tilfælde. Med Insertion Sort er tidskompleksiteten i bedste tilfælde O(n) og tog mindre end et millisekund for op til 524.288 elementer. Så i det bedste tilfælde er Insertion Sort for et hvilket som helst antal elementer en størrelsesorden hurtigere end Selection Sort.

n	Selektionssortering sorteret	Insættelsessortering sorteret	Selektionssortering nedadgående	Insættelsessortering nedadgående
…	…	…	…	…
16.384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65.536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

Og endnu en gang som diagram:

Insertion Sort er derfor ikke kun hurtigere end Selection Sort i det bedste tilfælde, men også i det gennemsnitlige og værste tilfælde.

Grunden hertil er, at Insertion Sort i gennemsnit kræver halvt så mange sammenligninger. Til minde om, at vi med Insertion Sort har sammenligninger og forskydninger, der i gennemsnit udgør op til halvdelen af de sorterede elementer; med Selection Sort skal vi søge efter det mindste element i alle usorterede elementer i hvert trin.

Selection Sort har betydeligt færre skriveoperationer, så Selection Sort kan være hurtigere, når skriveoperationer er dyre. Dette er ikke tilfældet med sekventielle skrivninger til arrays, da disse oftest foregår i CPU’ens cache.

I praksis anvendes Selection Sort derfor næsten aldrig.

Summary

Selection Sort er en let implementerbar og i den typiske implementering ustabil sorteringsalgoritme med en gennemsnitlig, best-case og worst-case tidskompleksitet på O(n²).

Selection Sort er langsommere end Insertion Sort, hvorfor den sjældent anvendes i praksis.

Du finder flere sorteringsalgoritmer i denne oversigt over alle sorteringsalgoritmer og deres egenskaber i den første del af artikelserien.

Hvis du kunne lide artiklen, er du velkommen til at dele den ved hjælp af en af deleknapperne til sidst. Ønsker du at blive informeret via e-mail, når jeg udgiver en ny artikel? Så brug nedenstående formular til at tilmelde dig mit nyhedsbrev.