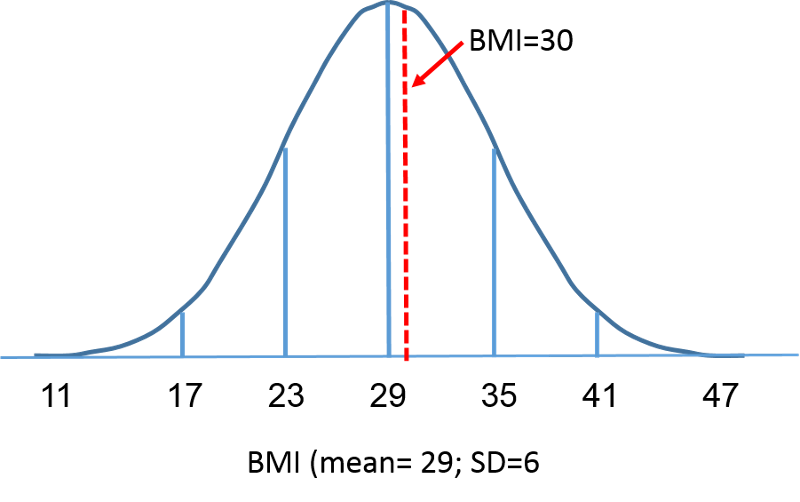
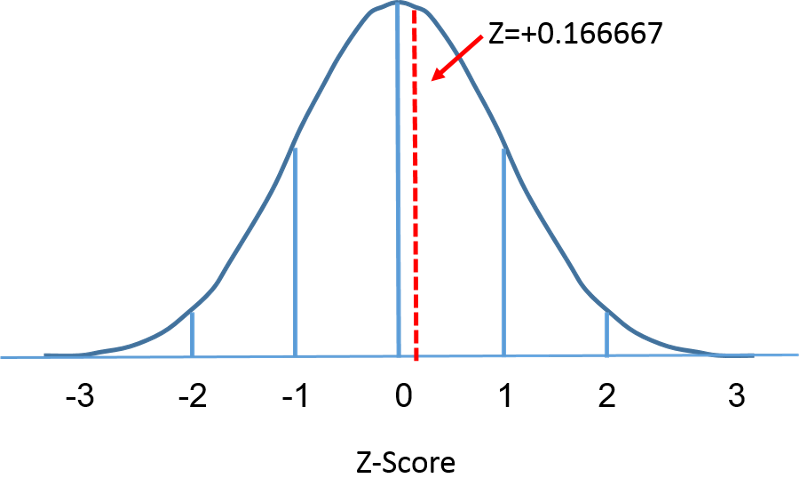
Standardnormalfordelingen er en normalfordeling med en middelværdi på nul og en standardafvigelse på 1. Standardnormalfordelingen er centreret på nul, og den grad, hvormed en given måling afviger fra middelværdien, er givet ved standardafvigelsen. For standardnormalfordelingen ligger 68 % af observationerne inden for 1 standardafvigelse fra middelværdien; 95 % ligger inden for 2 standardafvigelser fra middelværdien; og 99,9 % ligger inden for 3 standardafvigelser fra middelværdien. Indtil nu har vi brugt “X” til at betegne den pågældende variabel (f.eks. X=BMI, X=højde, X=vægt). Når vi anvender en standardnormalfordeling, vil vi imidlertid bruge “Z” til at betegne en variabel i forbindelse med en standardnormalfordeling. Efter standardisering er BMI=30, som blev diskuteret på den foregående side, vist nedenfor liggende 0,16667 enheder over middelværdien 0 på standardnormalfordelingen til højre.
 ====
====
Da arealet under standardkurven = 1, kan vi begynde at definere sandsynlighederne for en specifik observation mere præcist. For enhver given Z-score kan vi beregne arealet under kurven til venstre for denne Z-score. Tabellen i rammen nedenfor viser sandsynlighederne for standardnormalfordelingen. Undersøg tabellen og bemærk, at en “Z”-score på 0,0 angiver en sandsynlighed på 0,50 eller 50 %, og en “Z”-score på 1, dvs. en standardafvigelse over middelværdien, angiver en sandsynlighed på 0,8413 eller 84 %. Det skyldes, at en standardafvigelse over og under gennemsnittet omfatter ca. 68 % af arealet, så en standardafvigelse over gennemsnittet repræsenterer halvdelen af dette område, dvs. 34 %. Så de 50% under gennemsnittet plus de 34% over gennemsnittet giver os 84%.
Sandsynligheder for standardnormalfordelingen Z
![]()
Denne tabel er organiseret således, at den angiver arealet under kurven til venstre for eller mindre end en bestemt værdi eller “Z-værdi”. I dette tilfælde, fordi middelværdien er nul og standardafvigelsen er 1, er Z-værdien antallet af standardafvigelsesenheder væk fra middelværdien, og arealet er sandsynligheden for at observere en værdi mindre end den pågældende Z-værdi. Bemærk også, at tabellen viser sandsynligheder med to decimaler af Z. Enhedernes sted og det første decimaltal er vist i venstre kolonne, og det andet decimaltal er vist på tværs af den øverste række.
Men lad os vende tilbage til spørgsmålet om sandsynligheden for, at BMI er mindre end 30, dvs. P(X<30). Vi kan besvare dette spørgsmål ved hjælp af standardnormalfordelingen. Figurerne nedenfor viser fordelingerne af BMI for mænd på 60 år og standardnormalfordelingen side om side.
Fordeling af BMI og standardnormalfordeling
 ====
====
Overfladen under hver kurve er én, men skalaen på X-aksen er forskellig. Bemærk dog, at arealerne til venstre for den stiplede linje er de samme. BMI-fordelingen spænder fra 11 til 47, mens den standardiserede normalfordeling, Z, spænder fra -3 til 3. Vi ønsker at beregne P(X < 30). For at gøre dette kan vi bestemme den Z-værdi, der svarer til X = 30, og derefter bruge tabellen for den standardiserede normalfordeling ovenfor til at finde sandsynligheden eller arealet under kurven. Følgende formel omdanner en X-værdi til en Z-score, også kaldet en standardiseret score:

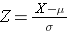
hvor μ er middelværdien og σ er standardafvigelsen for variablen X.
For at beregne P(X < 30) omregner vi X=30 til den tilsvarende Z-score (dette kaldes standardisering):

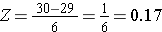
Det vil sige, P(X < 30) = P(Z < 0,17). Vi kan derefter slå den tilsvarende sandsynlighed for denne Z-score op i standardnormalfordelingstabellen, som viser, at P(X < 30) = P(Z < 0,17) = 0,5675. Sandsynligheden for, at en mand på 60 år har et BMI på under 30, er således 56,75 %.
Et andet eksempel
Hvad er sandsynligheden for, at en mand på 60 år har et BMI på over 35, hvis man bruger den samme fordeling for BMI? Med andre ord, hvad er P(X > 35)? Igen standardiserer vi:

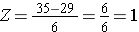
Vi går nu til standardnormalfordelingstabellen for at slå P(Z>1) op, og for Z=1,00 finder vi, at P(Z<1,00) = 0,8413. Bemærk dog, at tabellen altid angiver sandsynligheden for, at Z er mindre end den angivne værdi, dvs. at den giver os P(Z<1)=0,8413.
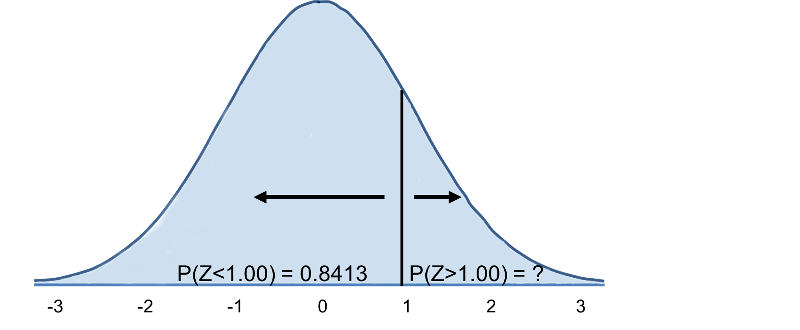
Dermed er P(Z>1)=1-0,8413=0,1587. Fortolkning: Næsten 16% af mænd på 60 år har et BMI over 35.
Normalsandsynlighedsberegner
![]()
![]()
Z-scorer med R
Som et alternativ til at slå normale sandsynligheder op i tabellen eller bruge Excel, kan vi bruge R til at beregne sandsynligheder. F.eks.
> pnorm(0)
En Z-score på 0 (middelværdien af en hvilken som helst fordeling) har 50 % af arealet til venstre. Hvad er sandsynligheden for, at en 60-årig mand i ovenstående population har et BMI på under 29 (middelværdien)? Z-score vil være 0, og pnorm(0)=0,5 eller 50 %.
Hvor stor er sandsynligheden for, at en 60-årig mand har et BMI på under 30? Z-score var 0,16667.
> pnorm(0,16667)
Så sandsynligheden er 56,6 %.
Hvad er sandsynligheden for, at en 60-årig mand vil have et BMI på over 35?
35-29=6, hvilket er en standardafvigelse over gennemsnittet. Så vi kan beregne arealet til venstre
> pnorm(1)
og derefter trække resultatet fra 1,0.
1-0,8413447= 0,1586553
Så sandsynligheden for, at en 60-årig mand har et BMI på over 35, er 15,8 %.
Og vi kan bruge R til at beregne det hele i et enkelt trin på følgende måde:
> 1-pnorm(1)
Sandsynlighed for et interval af værdier

Hvad er sandsynligheden for, at en mand på 60 år har et BMI mellem 30 og 35? Bemærk, at dette er det samme som at spørge, hvor stor en andel af mænd på 60 år der har et BMI mellem 30 og 35. Mere specifikt ønsker vi P(30 < X < 35)? Vi har tidligere beregnet P(30<X) og P(X<35); hvordan kan disse to resultater bruges til at beregne sandsynligheden for, at BMI vil ligge mellem 30 og 35? Prøv at formulere og svare på egen hånd, inden du ser på forklaringen nedenfor.
Svar