
Planter kan dyrke nye celler i spiraler, som f.eks. mønsteret af frø i denne smukke solsikke.
Spiralen sker naturligt, fordi hver ny celle dannes efter en drejning.
“Ny celle, så drejning,
så endnu en celle, så drejning, …”
Hvor langt skal man dreje?
Så, hvis du var en plante, hvor langt skulle du så dreje mellem nye celler?
Hvis du slet ikke drejer dig, får du en lige linje.
![]()
![]()
Men det er et meget dårligt design…. du vil have noget rundt, der holder sammen uden huller.
Hvorfor ikke prøve at finde den bedste værdi for dig selv?
Prøv forskellige værdier, som f.eks. 0,75, 0,9, 3,1416, 0,62 osv.
Husk, du forsøger at lave et mønster uden huller fra start til slut:
(I øvrigt er det ligegyldigt med den hele taldel, som 1. eller 5., for det er hele omdrejninger, der peger os tilbage i samme retning.)
Hvad fik du?
Hvis du fik noget, der ender som 0,618 (eller 0,382, som er 1 – 0,618), så “Tillykke, du er et vellykket medlem af planteriget!”
 |
Det er fordi det gyldne snit (1.61803…) er den bedste løsning, og det har solsikkeblomsten fundet ud af på sin egen naturlige måde. Forsøg det … det skulle se sådan ud. |
Hvorfor?
Alle tal, der er en simpel brøk (eksempel: 0.75 er 3/4, og 0,95 er 19/20 osv.) vil efter et stykke tid give et mønster af linjer, der stabler sig op, hvilket giver huller.
Men det gyldne snit (dets symbol er det græske bogstav Phi, vist til venstre) er en ekspert i ikke at være en brøk.
Det er et irrationelt tal (hvilket betyder, at vi ikke kan skrive det som en simpel brøk), men mere end det … det er så langt fra at være i nærheden af en brøk, som vi kan komme.
| Det er ikke nok at være irrationelt | ||
|---|---|---|
 |
Pi (3,141592654…), som også er irrationelt. Det har desværre en decimal meget tæt på 1/7 (= 0,142857…), så det ender med 7 arme. |
|
 |
e (2,71828…), som også er irrationel, virker heller ikke, fordi dens decimal er tæt på 5/7 (0,714285…), så den ender også med 7 arme. | |
Så, hvordan virker det gyldne snit?
| En af de særlige egenskaber ved det gyldne snit er, at det kan defineres i forhold til sig selv, som her: | ||
| (I tal: 1,61803… = 1 + 1/1,61803…) | ||
| Det kan udvides til denne brøk, der fortsætter i al evighed (kaldet en “fortsat brøk”): | ||
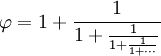 |
||
Sådan glider den pænt ind mellem simple brøker.
Fibonacci-tallene
Der er et særligt forhold mellem det gyldne snit og Fibonacci-tallene (0, 1, 1, 1, 2, 3, 3, 5, 8, 13, 21, … osv., hvert tal er summen af de to tal før det).
Når vi tager to på hinanden følgende (den ene efter den anden) Fibonacci-taller, er deres forhold meget tæt på det gyldne snit:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Så ligesom vi naturligt får syv arme, når vi bruger 0.142857 (1/7), har vi en tendens til at få Fibonacci-tal, når vi bruger det gyldne snit.
Forsøg at tælle spiralarmene – de “venstresvingende” spiraler og derefter de “højresvingende” spiraler … hvilke tal fik du?
Spiralformet bladvækst

Denne interessante adfærd findes ikke kun i solsikkefrø.
Lave, grene og kronblade kan også vokse i spiraler.
Hvorfor? For at nye blade ikke skal blokere for solen fra ældre blade, eller for at den maksimale mængde regn eller dug bliver ledt ned til rødderne.
Faktisk set, når en plante har spiraler, har rotationen en tendens til at være en brøk lavet med to på hinanden følgende (efter hinanden) Fibonacci-tal, for eksempel:
- En halv rotation er 1/2 (1 og 2 er Fibonacci-tal)
- 3/5 er også almindeligt (begge Fibonacci-tal), og
- 5/8 også (du gættede det!)
og alle kommer tættere og tættere på det gyldne snit.
|
Og derfor er Fibonacci-tallene meget almindelige i planter. Her er en marguerit med 21 kronblade |
 |
Men vi ser ikke dette hos alle planter, da naturen har mange forskellige metoder til at overleve.
Guldvinkel
Så vidt vi hidtil har talt om “omdrejninger” (fulde rotationer).
Det, der svarer til 0,61803… rotationer, er 222,4922… grader, eller ca. 222,5°.
I den anden retning er det ca. 137,5°, kaldet “den gyldne vinkel”.
Så næste gang du går i haven, så kig efter den gyldne vinkel,
og tæl kronblade og blade for at finde Fibonacci-tallene,
og opdag hvor kloge planterne er … !
Øvelse
Hvorfor går du ikke ud i haven eller parken lige nu, og begynder at tælle blade og kronblade og måle rotationer for at se, hvad du finder.
Du kan skrive dine resultater på denne formular:
| Plantens navn eller beskrivelse: | |||||
| Vokser bladene i spiraler? J / N | |||||
| Tæl en gruppe blade: | |||||
| Hvor mange blade (a) ? | |||||
| Hvor mange fulde omdrejninger (b) ? | |||||
| Rotation pr. blad (b/a) : | |||||
| Rotationsvinkel (360 × b/a) : | |||||
| Er der blomster? J / N | |||||
| Hvor mange kronblade på blomst 1: | |||||
| Blomst 3: | |||||
(Men husk, naturen har sine egne regler, og den behøver ikke at følge matematiske mønstre,
men når den gør det, er det fantastisk at se.)
* Noter om animationen
Solsikkefrø vokser fra midten og udad, men på animationen fandt jeg det nemmere at tegne de yngre frø først og tilføje de ældre.
Animationen skal fortsætte længere, så den er den samme som solsikkerheden – det ville resultere i 55 spiraler med uret og 34 spiraler mod uret (på hinanden følgende Fibonacci-tal). Jeg ville bare ikke have, at det skulle tage for lang tid.
Spiralerne er ikke programmeret ind i den – de opstår naturligt som følge af, at man forsøger at placere frøene så tæt på hinanden som muligt og samtidig holde dem i den korrekte rotation.

