Biografi
Johannes Kepler er nu hovedsageligt kendt for at have opdaget de tre love for planetarisk bevægelse, der bærer hans navn og blev offentliggjort i 1609 og 1619). Han udførte også vigtigt arbejde inden for optik (1604, 1611), opdagede to nye regelmæssige polyedre (1619), gav den første matematiske behandling af tæt pakning af lige store kugler (hvilket førte til en forklaring på formen af cellerne i en honeycomb, 1611), gav det første bevis for, hvordan logaritmer fungerer (1624), og udtænkte en metode til at finde rumfanget af omdrejningslegemer, som (set i bakspejlet!) kan ses som et bidrag til udviklingen af regnearket (1615, 1616). Desuden beregnede han de hidtil mest nøjagtige astronomiske tabeller, hvis fortsatte nøjagtighed i høj grad bidrog til at fastslå sandheden i den heliocentriske astronomi (Rudolphine Tables, Ulm, 1627).
En stor mængde af Keplers korrespondance er bevaret. Mange af hans breve svarer næsten til en videnskabelig artikel (der fandtes endnu ikke videnskabelige tidsskrifter), og korrespondenterne synes at have gemt dem, fordi de var interessante. Derfor ved vi en hel del om Keplers liv og om hans karakter. Det er til dels på grund af dette, at Kepler har haft noget af en karriere som en mere eller mindre fiktiv person (se historiografisk note nedenfor).
Kepler blev født i den lille by Weil der Stadt i Schwaben og flyttede med sine forældre til det nærliggende Leonberg i 1576. Hans far var lejesoldat og hans mor datter af en kroværtinde. Johannes var deres første barn. Hans far forlod hjemmet for sidste gang, da Johannes var fem år, og det menes, at han døde i krigen i Nederlandene. Som barn boede Kepler sammen med sin mor i sin bedstefars kro. Han fortæller, at han plejede at hjælpe til ved at tjene i kroen. Man kan forestille sig, at kunderne nogle gange var forvirrede over barnets usædvanlige kompetence i aritmetik.
Keplers tidlige uddannelse foregik i en lokal skole og derefter på et nærliggende seminarium, hvorfra han med henblik på at blive ordineret indskrev sig på universitetet i Tübingen, der dengang (som nu) var en bastion for luthersk ortodoksi.
Keplers holdninger
Kepler var hele sit liv en dybt religiøs mand. Alle hans skrifter indeholder talrige henvisninger til Gud, og han så sit arbejde som en opfyldelse af sin kristne pligt til at forstå Guds gerninger. Da mennesket, som Kepler mente, var skabt i Guds billede, var det klart, at det var i stand til at forstå det univers, som han havde skabt. Desuden var Kepler overbevist om, at Gud havde skabt universet efter en matematisk plan (en tro, der findes i Platons værker og forbindes med Pythagoras). Da det dengang var almindeligt accepteret, at matematikken var en sikker metode til at finde frem til sandheder om verden (Euklids almindelige begreber og postulater blev anset for at være reelt sande), har vi her en strategi til at forstå universet. Da nogle forfattere har givet Kepler et navn for irrationalitet, er det værd at bemærke, at denne ret håbefulde epistemologi faktisk ligger meget langt fra mystikerens overbevisning om, at tingene kun kan forstås på en upræcis måde, der er afhængig af indsigter, der ikke er underlagt fornuften. Kepler takker ganske vist gentagne gange Gud for at have givet ham indsigt, men indsigten præsenteres som rationel.
Universitetsuddannelse
På denne tid var det almindeligt, at alle studerende på et universitet skulle følge kurser i “matematik”. I princippet omfattede dette de fire matematiske videnskaber: aritmetik, geometri, astronomi og musik. Det ser dog ud til, at det afhang af det enkelte universitet, hvad der blev undervist i. I Tübingen blev Kepler undervist i astronomi af en af datidens førende astronomer, Michael Mästlin (1550 – 1631). Undervisningens astronomi var naturligvis geocentrisk astronomi, dvs. den aktuelle version af det ptolemæiske system, hvor alle syv planeter – Månen, Merkur, Venus, Solen, Mars, Jupiter og Saturn – bevægede sig rundt om Jorden, og hvor deres positioner i forhold til de faste stjerner blev beregnet ved at kombinere deres cirkelbevægelser. Dette system var mere eller mindre i overensstemmelse med de gældende (aristoteliske) opfattelser af fysik, selv om der var visse vanskeligheder, såsom hvorvidt man kunne betragte en cirkelbevægelse, der ikke var ensartet omkring sit eget centrum, men omkring et andet punkt (kaldet en “ækvant”), som “ensartet” (og derfor acceptabel som åbenbart evig). Det ser dog ud til, at astronomerne (som så sig selv som “matematikere”) i det store og hele var tilfredse med at fortsætte med at beregne planeternes positioner og overlade det til naturfilosofferne at bekymre sig om, hvorvidt de matematiske modeller svarede til de fysiske mekanismer. Kepler indtog ikke denne holdning. Hans tidligste offentliggjorte værk (1596) foreslår at overveje planeternes faktiske baner, ikke de cirkler, der blev brugt til at konstruere dem.
I Tübingen studerede Kepler ikke kun matematik, men også græsk og hebraisk (begge nødvendige for at kunne læse skrifterne på deres originalsprog). Undervisningen foregik på latin. Ved afslutningen af sit første år fik Kepler 10-taller for alt undtagen matematik. Sandsynligvis forsøgte Mästlin at fortælle ham, at han kunne gøre det bedre, for Kepler var faktisk en af de udvalgte elever, som han valgte at undervise i mere avanceret astronomi ved at introducere dem til Copernicus’ nye, heliocentriske kosmologiske system. Det var fra Mästlin, at Kepler fik at vide, at forordet til Om revolutionerne, hvori han forklarede, at der var tale om “kun matematik”, ikke var skrevet af Kopernikus. Kepler synes næsten øjeblikkeligt at have accepteret, at det kopernikanske system var fysisk sandt; hans grunde til at acceptere det vil blive diskuteret i forbindelse med hans første kosmologiske model (se nedenfor).
Det ser ud til, at der allerede i Keplers studietid var tegn på, at hans religiøse overbevisning ikke var helt i overensstemmelse med den ortodokse lutheranisme, der var fremherskende i Tübingen og formuleret i Confessio Augustana Ⓣ. Keplers problemer med denne protestantiske ortodoksi vedrørte det formodede forhold mellem materie og “ånd” (en ikke-materiel enhed) i doktrinen om eukaristien. Dette hænger sammen med Keplers astronomi i det omfang, at han tilsyneladende havde lidt lignende intellektuelle vanskeligheder med at forklare, hvordan “kraft” fra solen kunne påvirke planeterne. I sine skrifter er Kepler tilbøjelig til at sætte sine holdninger på spidsen – hvilket er meget bekvemt for historikere. I det virkelige liv er det sandsynligt, at en lignende tendens til åbenhed fik myndighederne i Tübingen til at nære begrundet tvivl om hans religiøse ortodoksi. Dette kan forklare, hvorfor Mästlin overtalte Kepler til at opgive sine planer om at blive ordineret og i stedet tage en stilling som matematiklærer i Graz. Den religiøse intolerance blev skærpet i de følgende år. Kepler blev ekskommunikeret i 1612. Det gjorde ham meget ondt, men på trods af hans (på det tidspunkt) relativt høje sociale status som kejserlig matematiker lykkedes det ham aldrig at få forbuddet ophævet.
Keplers første kosmologiske model (1596)
I stedet for de syv planeter i den almindelige geocentriske astronomi havde det kopernikanske system kun seks, idet månen var blevet et legeme af en art, som astronomien hidtil ikke havde kendt, og som Kepler senere skulle kalde en “satellit” (et navn, som han opfandt i 1610 for at beskrive de måner, som Galilei havde opdaget kredsede om Jupiter, og som bogstaveligt talt betyder “ledsager”). Hvorfor seks planeter?
I den geocentriske astronomi var der desuden ingen mulighed for at bruge observationer til at finde de relative størrelser af de planetariske kugler; man antog simpelthen, at de var i kontakt med hinanden. Dette syntes ikke at kræve nogen forklaring, da det passede fint med naturfilosoffernes tro på, at hele systemet blev drejet ud fra bevægelsen af den yderste kugle, en (eller måske to) ud over de “faste” stjerners kugle (dem, hvis mønster dannede stjernebillederne), ud over Saturns kugle. I det kopernikanske system gjorde det faktum, at den årlige komponent af hver planeters bevægelse var en afspejling af Jordens årlige bevægelse, det muligt at bruge observationer til at beregne størrelsen af hver planets bane, og det viste sig, at der var enorme rum mellem planeterne. Hvorfor netop disse mellemrum?
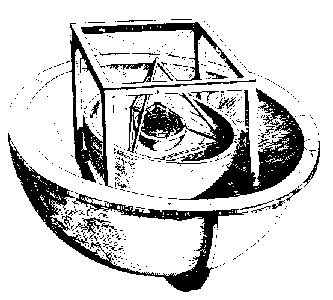
Keplers svar på disse spørgsmål, der er beskrevet i hans Mysterium cosmographicum Ⓣ, Tübingen, 1596, ser bizart ud for læsere i det tyvende århundrede (se figuren til højre). Han foreslog, at hvis en kugle blev tegnet så den rørte Saturns bane indvendigt, og en terning blev indskrevet i kuglen, så ville den kugle, der var indskrevet i denne terning, være den kugle, der omskrev Jupiters bane. Hvis der så blev tegnet et regulært tetraeder i den kugle, der indskriver Jupiters bane, ville tetraederets indersfære være den kugle, der omskriver Mars’ bane, og så videre indad, så der kom det regulære dodekaeder mellem Mars og Jorden, det regulære isosaeder mellem Jorden og Venus og det regulære oktaeder mellem Venus og Merkur. Dette forklarer antallet af planeter perfekt: der findes kun fem konvekse regulære faste legemer (som det er bevist i Euklids Elementer , bog 13). Det giver også en overbevisende overensstemmelse med størrelsen af banerne som udledt af Kopernikus, idet den største fejl er mindre end 10 % (hvilket selv i dag er spektakulært godt for en kosmologisk model). Kepler udtrykte sig ikke i procentvise fejl, og hans er faktisk den første matematiske kosmologiske model, men det er let at se, hvorfor han mente, at observationerne støttede hans teori.
Kepler så sin kosmologiske teori som et bevis for den kopernikanske teori. Inden han præsenterede sin egen teori, gav han argumenter for at fastslå plausibiliteten af selve den kopernikanske teori. Kepler hævder, at dens fordele i forhold til den geocentriske teori ligger i dens større forklaringskraft. F.eks. kan den kopernikanske teori forklare, hvorfor Venus og Merkur aldrig ses meget langt fra Solen (de ligger mellem Jorden og Solen), mens der i den geocentriske teori ikke er nogen forklaring på dette forhold. Kepler opregner ni sådanne spørgsmål i det første kapitel af Mysterium cosmographicum Ⓣ.
Kepler udførte dette arbejde, mens han underviste i Graz, men bogen blev set gennem trykken i Tübingen af Mästlin. Overensstemmelsen med de værdier, der blev udledt af observationer, var ikke nøjagtig, og Kepler håbede, at bedre observationer ville forbedre overensstemmelsen, så han sendte et eksemplar af Mysterium cosmographicum til en af tidens førende observationsastronomer, Tycho Brahe (1546 – 1601). Tycho, der dengang arbejdede i Prag (på det tidspunkt hovedstaden i det Hellige Romerske Rige), havde faktisk allerede skrevet til Mästlin for at få en matematisk assistent. Kepler fik jobbet.
“Krigen mod Mars”
Naturligvis var Tychos prioriteringer ikke de samme som Keplers, og Kepler kom snart til at arbejde med det uløselige problem med Mars’ bane. Han fortsatte med at arbejde på dette efter Tychos død (i 1601), og Kepler efterfulgte ham som kejserlig matematiker. Konventionelt set var baner sammensat af cirkler, og der var ret få observationsværdier nødvendige for at fastsætte cirklernes relative radier og positioner. Tycho havde foretaget et enormt antal observationer, og Kepler var fast besluttet på at gøre bedst mulig brug af dem. I det væsentlige havde han så mange observationer til rådighed, at når han først havde konstrueret en mulig bane, var han i stand til at kontrollere den mod yderligere observationer, indtil der blev opnået en tilfredsstillende enighed. Kepler konkluderede, at Mars’ bane var en ellipse med Solen i et af brændpunkterne (et resultat, der, når det udvides til alle planeterne, nu kaldes “Keplers første lov”), og at en linje, der forbinder planeten med Solen, udviskede lige store områder på lige lange tidspunkter, mens planeten beskrev sin bane (“Keplers anden lov”), dvs. at arealet bruges som et mål for tiden. Efter at dette arbejde blev offentliggjort i Astronomia nova, … Ⓣ, Heidelberg, 1609, fandt Kepler baner for de andre planeter og fastslog dermed, at de to love også gjaldt for dem. Begge love relaterer planetens bevægelse til Solen; Keplers kopernikanisme var afgørende for hans ræsonnement og for hans udledninger.
Den egentlige beregningsproces for Mars var enormt besværlig – der er næsten tusind overlevende folioark med regnestykker – og Kepler selv omtaler dette arbejde som “min krig med Mars”, men resultatet var en bane, der stemmer så nøjagtigt overens med moderne resultater, at man ved sammenligningen må tage højde for sekulære ændringer i banen siden Keplers tid.
Observationsfejl
Det var afgørende for Keplers metode til at kontrollere mulige baner i forhold til observationer, at han havde en idé om, hvad der skulle accepteres som tilstrækkelig overensstemmelse. Heraf udspringer den første eksplicitte brug af begrebet observationsfejl. Kepler kan have skyldt dette begreb i det mindste delvist til Tycho, som foretog detaljerede kontroller af sine instrumenters ydeevne (se biografien om Brahe).
Optik og den nye stjerne i 1604
Arbejdet om Mars var i det væsentlige afsluttet i 1605, men der var forsinkelser med at få bogen udgivet. I mellemtiden, som svar på bekymringer om månens forskellige tilsyneladende diameter, når den observeres direkte og når den observeres ved hjælp af en camera obscura, arbejdede Kepler en del med optik og kom med den første korrekte matematiske teori om camera obscura og den første korrekte forklaring på det menneskelige øjes funktion, med et omvendt billede dannet på nethinden. Disse resultater blev offentliggjort i Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Frankfurt, 1604. Han skrev også om den nye stjerne fra 1604, som nu normalt kaldes “Keplers supernova”, idet han afviste adskillige forklaringer og på et tidspunkt bemærkede, at denne stjerne selvfølgelig bare kunne være en særlig skabelse “men før vi kommer til det, tror jeg, at vi bør prøve alt andet” De stella nova Ⓣ, Prag, 1606, kapitel 22, KGW 1, s. 257, linje 23.
I forlængelse af Galileis brug af teleskopet til at opdage Jupiters måner, offentliggjort i hans Sidereal Messenger (Venedig, 1610), som Kepler havde skrevet et entusiastisk svar på (1610), skrev Kepler en undersøgelse af linsernes egenskaber (det første arbejde af denne art om optik), hvori han præsenterede en ny konstruktion af teleskopet, hvor han brugte to konvekse linser (Dioptrice, Prag, 1611). Dette design, hvor det endelige billede er omvendt, var så vellykket, at det nu normalt ikke er kendt som et kepleriansk teleskop, men blot som det astronomiske teleskop.
Afgang fra Prag til Linz
Keplers år i Prag var relativt fredelige og videnskabeligt set yderst produktive. Faktisk synes han aldrig at have ladet ydre omstændigheder forhindre ham i at komme videre med sit arbejde, selv når tingene gik dårligt. Det begyndte at gå meget dårligt i slutningen af 1611. Først døde hans syvårige søn. Kepler skrev til en ven, at dette dødsfald var særlig svært at bære, fordi barnet mindede ham så meget om ham selv i den alder. Så døde Keplers kone. Derefter blev kejser Rudolf, hvis helbred var svækket, tvunget til at abdicere til fordel for sin bror Matthias, der ligesom Rudolf var katolik, men som (i modsætning til Rudolf) ikke troede på tolerance over for protestanter. Kepler var nødt til at forlade Prag. Inden han rejste, fik han flyttet sin hustrus lig over i sønnens grav og skrev et latinsk gravskrift til dem. Han og hans resterende børn flyttede til Linz (nu i Østrig).
Egteskab og vinfade
Kepler synes at have giftet sig med sin første kone, Barbara, af kærlighed (selvom ægteskabet var arrangeret gennem en mægler). Det andet ægteskab, i 1613, var et spørgsmål om praktisk nødvendighed; han havde brug for nogen til at passe børnene. Keplers nye hustru, Susanna, fik et lynkursus i Keplers karakter: i dedikationsbrevet til den efterfølgende bog forklares det, at han under bryllupsfesten bemærkede, at vinfadernes volumen blev anslået ved hjælp af en stang, der blev skråt indført gennem spunshullet, og at han begyndte at undre sig over, hvordan det kunne fungere. Resultatet blev en undersøgelse af rumfanget af omdrejningslegemer Nova stereometria doliorum … Ⓣ, Linz, 1615, hvor Kepler med udgangspunkt i Archimedes’ arbejde anvendte en opløsning i “indivisibles”. Denne metode blev senere udviklet af Bonaventura Cavalieri (ca. 1598 – 1647) og er en del af forfædrene til infinitesimalregningen.
The Harmony of the World
Keplers hovedopgave som kejserlig matematiker var at skrive astronomiske tabeller, baseret på Tychos observationer, men det han egentlig ønskede at gøre var at skrive The Harmony of the World, planlagt siden 1599 som en udvikling af hans Mystery of the Cosmos. Dette andet værk om kosmologi (Harmonices mundi libri V Ⓣ, Linz, 1619) præsenterer en mere udførlig matematisk model end den tidligere, selv om polyederne stadig er der. Matematikken i dette værk omfatter den første systematiske behandling af tessellationer, et bevis for, at der kun findes tretten konvekse ensartede polyedre (de arkimediske faste legemer), og den første redegørelse for to ikke-konvekse regelmæssige polyedre (alle i bog 2). The Harmony of the World indeholder også det, der nu er kendt som “Keplers tredje lov”, nemlig at for to planeter vil forholdet mellem kvadraterne af deres perioder være det samme som forholdet mellem terningerne af de gennemsnitlige radier af deres baner. Fra den første havde Kepler søgt efter en regel, der relaterer banernes størrelse til perioderne, men der var ingen langsom række af skridt hen imod denne lov, som der havde været hen imod de to andre. Faktisk, selv om den tredje lov spiller en vigtig rolle i nogle af de sidste afsnit i den trykte udgave af Harmony of the World, blev den faktisk ikke opdaget, før værket var under tryk. Kepler foretog revisioner i sidste øjeblik. Han fortæller selv historien om den endelige succes:
…og hvis du vil have det nøjagtige tidspunkt, så blev den mentalt udtænkt den 8. marts i dette år et tusind seks hundrede og atten, men underkastet beregningen på en uheldig måde, og derfor afvist som falsk, og endelig vendte den tilbage den 15. maj og vedtog en ny angrebslinje, stormede mørket i mit sind. Så stærk var støtten fra kombinationen af mit syttenårige arbejde med Brahes observationer og den foreliggende undersøgelse, som konspirerede sammen, at jeg først troede, at jeg drømte og antog min konklusion blandt mine grundlæggende forudsætninger. Men det er helt sikkert og nøjagtigt, at “forholdet mellem de periodiske tider for to planeter er netop det sesquialterate forhold mellem deres gennemsnitlige afstande …”
(Harmonice mundi Book 5, Chapter 3, trans. Aiton, Duncan and Field, p. 411).
Retssag om hekseri
Mens Kepler arbejdede på sin Harmony of the World, blev hans mor anklaget for hekseri. Han tilkaldte hjælp fra det juridiske fakultet i Tübingen. Katharina Kepler blev til sidst løsladt, i det mindste delvis som følge af tekniske indvendinger, der skyldtes myndighedernes manglende overholdelse af de korrekte juridiske procedurer i forbindelse med anvendelsen af tortur. De overlevende dokumenter er skræmmende. Kepler fortsatte imidlertid med at arbejde. I kusken læste han på sin rejse til Württemberg for at forsvare sin mor et værk om musikteori af Vincenzo Galilei (ca. 1520 – 1591, Galileos far), som der er talrige henvisninger til i The Harmony of the World.
Astronomiske tabeller
Beregning af tabeller, den normale beskæftigelse for en astronom, involverede altid tung aritmetik. Kepler var derfor meget glad, da han i 1616 stødte på Napiers arbejde om logaritmer (udgivet i 1614). Mästlin fortalte ham imidlertid straks, at det for det første var upassende for en seriøs matematiker at glæde sig over et simpelt hjælpemiddel til beregning, og for det andet at det var uklogt at stole på logaritmer, fordi ingen forstod, hvordan de virkede. (Lignende bemærkninger blev fremsat om computere i begyndelsen af 1960’erne.) Keplers svar på den anden indvending var at offentliggøre et bevis for, hvordan logaritmer virkede, baseret på en upåklageligt respektabel kilde: Euklids Elementer bog 5. Kepler beregnede tabeller med ottecifrede logaritmer, som blev offentliggjort med Rudolphine-tabellerne (Ulm, 1628). De astronomiske tabeller anvendte ikke kun Tychos observationer, men også Keplers to første love. Alle astronomiske tabeller, der gjorde brug af nye observationer, var nøjagtige i de første par år efter offentliggørelsen. Det bemærkelsesværdige ved Rudolphine-tabellerne var, at de viste sig at være nøjagtige over årtier. Og efterhånden som årene blev ophobet, blev tabellernes fortsatte nøjagtighed naturligvis set som et argument for korrektheden af Keplers love og dermed for korrektheden af den heliocentriske astronomi. Keplers opfyldelse af sin kedelige officielle opgave som kejserlig matematiker førte til opfyldelsen af hans inderste ønske, nemlig at hjælpe med at etablere kopernikanismen.
Wallenstein
Men da de rudolphinske tabeller blev offentliggjort, arbejdede Kepler faktisk ikke længere for kejseren (han havde forladt Linz i 1626), men for Albrecht von Wallenstein (1583 – 1632), en af de få succesfulde militære ledere i Trediveårskrigen (1618 – 1648).
Wallenstein forventede, ligesom kejser Rudolf, at Kepler ville give ham råd baseret på astrologi. Kepler måtte naturligvis adlyde, men påpeger gentagne gange, at han ikke tror på, at man kan lave præcise forudsigelser. Som de fleste mennesker på den tid accepterede Kepler astrologiens princip om, at himmellegemerne kunne påvirke det, der skete på Jorden (de tydeligste eksempler er solen, der forårsager årstiderne, og månen, der forårsager tidevandet), men som kopernikaner troede han ikke på stjernebilledernes fysiske virkelighed. Hans astrologi var kun baseret på vinklerne mellem himmellegemernes positioner (“astrologiske aspekter”). Han udtrykker dyb foragt for de komplicerede systemer i den konventionelle astrologi.
Død
Kepler døde i Regensburg efter en kortvarig sygdom. Han opholdt sig i byen på vej til at indkassere nogle penge, som han skyldte ham i forbindelse med Rudolphine-tabellerne. Han blev begravet i den lokale kirke, men denne blev ødelagt i løbet af Trediveårskrigen, og der er intet tilbage af graven.
Historiografisk note
Der er undertiden blevet gjort meget ud af angiveligt ikke-rationelle elementer i Keplers videnskabelige aktivitet. Troende astrologer hævder ofte, at hans arbejde udgør en videnskabeligt respektabel forløber for deres eget arbejde. I sin indflydelsesrige Sleepwalkers gjorde den afdøde Arthur Koestler Keplers kamp med Mars til et argument for den moderne videnskabs iboende irrationalitet. Der har været mange stiltiende tilhængere af disse to overbevisninger. Begge er imidlertid baseret på en meget partiel læsning af Keplers værk. Især synes Koestler ikke at have haft den matematiske ekspertise til at forstå Keplers fremgangsmåder. Nærmere studier viser, at Koestler simpelthen tog fejl i sin vurdering.
Det virkelig vigtige ikke-rationelle element i Keplers arbejde er hans kristendom. Keplers omfattende og vellykkede brug af matematik får hans arbejde til at se “moderne” ud, men vi har i virkeligheden at gøre med en kristen naturfilosof, for hvem forståelsen af universets natur også omfattede forståelsen af dets skabers natur.