I tabellen over frekvenser nedenfor kan du finde A = 440 Hz, og derefter
A# = 466,16 Hz,
B = 493,88 Hz,
C = 523,25 Hz osv.
Der kan også findes C i midten: 261.63 Hz.
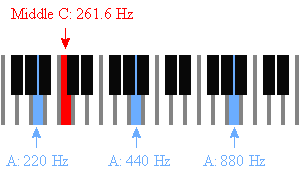
Tabel over musikalske frekvenser
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
130.82
138.59
146.83
155.56
164.81
174.61
185
196
207.65
220
233.08
246.94
Note
C
C#
D
D#
D#
E
F
F#
G
G#
G#
A
A#
A#
B
Frekvens
261.63
277.18
293.66
311.13
329.63
349.23
369.99
392
415.3
440
466.16
493.88
Note
C
C#
D
D#
D#
E
F
F#
G
G#
A
A#
A#
B
Frekvens
523.25
554.37
587.33
622.25
659.26
698.46
739.99
783.99
830.61
880
932.33
987.77
Note
C
C#
D
D#
D#
E
F
F#
G
G#
A
A
A#
B
C
Frekvens
1046.5
1108.73
1174.66
1244.51
1318.51
1396.91
1479.98
1567.98
1661.22
1760
1864.66
1975.53
2093.00
Disse er fundet ved hjælp af
frekvens `= 440×2^(n”/”12)`
for `n = -21, -19, …, 27`
Hvor kommer denne formel fra?
Denne opgave mindede mig om den sammensatte rente, som vi mødte tidligere i pengematematik. Frekvensen skal fordobles hver `12` tone (fordi der er `7` hvide toner og `5` sorte toner i hver oktav.)
Her er en graf over dette forhold:
frekvens `= 440×2^(n”/”12)`
Dette er en eksponentiel kurve, som vi tidligere har mødt i Grafer over eksponentielle funktioner.
Lige tempereret tuning
Et interessant problem har musikinstrumentmagere stået over for i hundredvis af år. For at få en “perfekt femtedel” (f.eks. intervallet mellem A og E ovenfor) skal vi spille en tone, der har `1,5` gange frekvensen af A.
På en violin (eller bratsch eller et hvilket som helst båndløst strengeinstrument) er dette muligt, og vi kan spille et smukt, perfekt E på `440 × 1,5 = 660\ “Hz”`. Men bemærk (ud fra ovenstående frekvenstabel), at et klaver, der spiller den samme tone, vil spille E `= 659,26\ “Hz”` .
For omkring 400 år siden blev klaviaturer (normalt cembalo og orgel) stemt til en bestemt gruppe af tangenter, så alle instrumenter, især strygere, lød “rigtigt” i disse tangenter. Cembaloet lød godt i disse tonearter, men ret forfærdeligt i andre tonearter uden relation til hinanden (f.eks. B-dur).
Der var faktisk flere forskellige stemmesystemer i brug på Bachs tid, bl.a. meantone (som havde til formål at få 3-dur 3rd. til at lyde godt, men som ikke var lige så bekymret for kvaliteten af store 5-dur 5d., med den virkning, at nogle tangenter ikke kunne bruges) og Werckmeisters 1691-stemning, som gjorde det muligt for komponisterne at skabe musik i alle tangenter (med den virkning, at de forskellige tangenter havde en forskellig klanglig kvalitet).
I begyndelsen af det 20. århundrede blev det besluttet at stemme tastaturer, så tonerne var jævnt fordelt (som de frekvenser, der er angivet i ovenstående tabel). Dette kaldes lige tempereret stemning. En sådan stemning var kendt på Bachs tid, men blev forkastet, fordi den blev anset for at være for “intetsigende” (alle tangenter har samme tonekvalitet), og fordi der ikke fandtes frekvensmålingsværktøjer, der ville have gjort det muligt at foretage nøjagtige stemninger.
Uheldigvis betyder lige tempereret stemning, at alle strengeinstrumenter skal tage højde for de små forskelle i stemninger mellem instrumenter, når der også er tale om keyboards. Strenge er normalt mest lykkelige, når de kun spiller med andre strenge af denne grund.
top
Søg IntMath
Online Trigonometry Solver
Denne trigonometri-løser kan løse en bred vifte af matematiske problemer.
Gå til: Online trigonometri-løser