Block cipher-tilstand

Autentificeret kryptering med yderligere data (AEAD) tilstandeRediger

En række funktionsmåder er blevet designet til at kombinere hemmeligholdelse og autentificering i en enkelt kryptografisk primitiv. Eksempler på sådanne tilstande er extended cipher block chaining (XCBC), integrity-aware cipher block chaining (IACBC), integrity-aware parallelizable mode (IAPM), OCB, EAX, CWC, CCM og GCM. Autentificerede krypteringstilstande klassificeres som single-pass-tilstande eller double-pass-tilstande. Nogle autentificerede krypteringsalgoritmer med en enkelt passage, som f.eks. OCB-tilstand, er behæftet med patenter, mens andre er specielt designet og frigivet på en måde, der gør det muligt at undgå en sådan behæftelse.

Dertil kommer, at nogle tilstande også giver mulighed for autentificering af ukrypterede tilknyttede data, og disse kaldes AEAD-ordninger (autentificeret kryptering med tilknyttede data). EAX-tilstand er f.eks. en AEAD-ordning med dobbelt passage, mens OCB-tilstand er en enkelt passage.

Galois/counter (GCM)Rediger

GCM

Galois/counter

Kryptering kan paralleliseres

Ja

Dekryptering paralleliserbar

Ja

Random læseadgang

Ja

Galois/counter-tilstand (GCM) kombinerer de velkendte counter-tilstand for kryptering med den nye Galois-tilstand for autentificering. Den vigtigste egenskab er, at det er let at parallelberegne den Galois-feltmultiplikation, der anvendes til autentificering. Denne egenskab giver mulighed for højere gennemløb end krypteringsalgoritmer.

GCM er defineret for blokchifre med en blokstørrelse på 128 bit. Galois message authentication code (GMAC) er en variant af GCM, der kun er beregnet til autentifikation, og som kan danne en inkrementel kode til autentifikation af meddelelser. Både GCM og GMAC kan acceptere initialiseringsvektorer af vilkårlig længde. GCM kan drage fuld fordel af parallel behandling, og ved at implementere GCM kan der gøres effektiv brug af en instruktionspipeline eller en hardwarepipeline. CBC-operationsmåden medfører pipeline-stallinger, der hæmmer dens effektivitet og ydeevne.

Som i CTR nummereres blokkene fortløbende, hvorefter dette bloknummer kombineres med en IV og krypteres med en blokchiffer E, normalt AES. Resultatet af denne kryptering XOR-opereres derefter med klarteksten for at fremstille krypteringsteksten. Som alle counter modes er dette i det væsentlige en stream cipher, og det er derfor vigtigt, at der anvendes en anden IV for hver stream, der krypteres.

Den krypterede tekstblokke betragtes som koefficienter af et polynomium, som derefter evalueres i et nøgleafhængigt punkt H ved hjælp af finite field aritmetik. Resultatet krypteres derefter og giver et autentifikationsmærke, der kan bruges til at verificere dataenes integritet. Den krypterede tekst indeholder derefter IV, ciffertekst og autentifikationsmærke.

Counter with cipher block chaining message authentication code (CCM)Edit

Counter with cipher block chaining message authentication code (counter with CBC-MAC; CCM) er en autentificeret krypteringsalgoritme, der er designet til at give både autentificering og fortrolighed. CCM-tilstand er kun defineret for blokchifre med en bloklængde på 128 bit.

Syntetisk initialiseringsvektor (SIV)Rediger

Syntetisk initialiseringsvektor (SIV) er en blokchifretilstand, der er modstandsdygtig over for misbrug af nonce.

SIV syntetiserer en intern IV ved hjælp af en pseudorandomfunktion S2V. S2V er en nøglebaseret hash er baseret på CMAC, og input til funktionen er:

• Supplerende autentificerede data (nul, et eller mange AAD-felter understøttes)
• Plaintext
• Autentifikationsnøgle (K1).

SIV krypterer S2V-udgangen og klarteksten ved hjælp af AES-CTR med krypteringsnøglen (K2).

SIV kan understøtte ekstern nonce-baseret autentiseret kryptering, i hvilket tilfælde et af de autentiserede datafelter udnyttes til dette formål. RFC5297 specificerer, at af hensyn til interoperabilitet bør det sidste autentificerede datafelt anvendes som ekstern nonce.

På grund af brugen af to nøgler, autentifikationsnøglen K1 og krypteringsnøglen K2, kan navneskemaer for SIV AEAD-varianter føre til en vis forvirring; f.eks. henviser AEAD_AES_AES_SIV_CMAC_256 til AES-SIV med to AES-128-nøgler og ikke AES-256.

AES-GCM-SIVEdit

AES-GCM-SIV er en driftsform for Advanced Encryption Standard, som giver samme ydeevne som Galois/counter-tilstand samt modstandsdygtighed over for misbrug i tilfælde af genbrug af en kryptografisk nonce. Konstruktionen er defineret i RFC 8452.

AES-GCM-SIV syntetiserer den interne IV. Den udleder en hash af de yderligere autentificerede data og klartekst ved hjælp af POLYVAL Galois-hashfunktionen. Hash-koden krypteres derefter en AES-nøgle og bruges som autentifikationsmærke og AES-CTR-initialiseringsvektor.

AES-GCM-SIV er en forbedring af den meget enslydende algoritme GCM-SIV med nogle få meget små ændringer (f.eks. hvordan AES-CTR initialiseres), men som giver praktiske fordele for dens sikkerhed “Denne tilføjelse gør det muligt at kryptere op til 250 meddelelser med den samme nøgle, sammenlignet med den betydelige begrænsning på kun 232 meddelelser, som var tilladt med GCM-SIV.”

Kun tilstande for fortrolighedRediger

Der er defineret mange driftstilstande. Nogle af disse er beskrevet nedenfor. Formålet med krypteringstilstande er at maskere mønstre, der findes i krypterede data, som illustreret i beskrivelsen af ECB’s svaghed.

Differente krypteringstilstande maskerer mønstre ved at kaskadere output fra krypteringsblokken eller andre globalt deterministiske variabler ind i den efterfølgende krypteringsblok. Indgangene for de anførte tilstande er opsummeret i følgende tabel:

Summary of modes

Mode		Formler	Ciphertext
Elektronisk kodebog	(ECB)	Yi = F(PlainTexti, Key)	Yi
Cipher block chaining	(CBC)	Yi = PlainTexti XOR Ciphertexti-1	F(Y, Key); Ciphertext0 = IV
Propagating CBC	(PCBC)	Yi = PlainTexti XOR (Ciphertexti-1 XOR PlainTexti-1)	F(Y, Key); Ciphertext0 = IV
Cipher feedback	(CFB)	Yi = Ciphertexti-1	Plaintext XOR F(Y, Key); Ciphertext0 = IV
Output feedback	(OFB)	Yi = F(Yi-1, Key); Y0 = F(IV, Key)	Plaintext XOR Yi
Counter	(CTR)	Yi = F(IV + g(i), Key); IV = token()	Plaintext XOR Yi

Note: g(i) er en vilkårlig deterministisk funktion, ofte identitetsfunktionen.

Elektronisk kodebog (ECB)Rediger

ECB

Elektronisk kodebog

Kryptering kan paralleliseres

Ja

Dekryptering kan paralleliseres

Ja

Random read access

Ja

Den enkleste af krypteringsformerne er den elektroniske kodebog (ECB) (opkaldt efter konventionelle fysiske kodebøger). Meddelelsen opdeles i blokke, og hver blok krypteres separat.

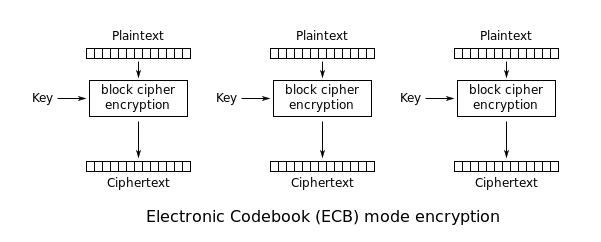
Ulempen ved denne metode er en manglende udbredelse. Fordi ECB krypterer identiske klartekstblokke til identiske ciphertekstblokke, skjuler den ikke datamønstre godt. ECB anbefales ikke til brug i kryptografiske protokoller.

Et slående eksempel på, i hvor høj grad ECB kan efterlade klartekstdatamønstre i cipherteksten, kan ses, når ECB-tilstanden bruges til at kryptere et bitmap-billede, der bruger store områder med ensartede farver. Selv om farven på hver enkelt pixel er krypteret, kan det samlede billede stadig skelnes, da mønsteret af identisk farvede pixels i originalen forbliver i den krypterede version.

ECB-tilstand kan også gøre protokoller uden integritetsbeskyttelse endnu mere modtagelige for replay-angreb, da hver blok bliver dekrypteret på nøjagtig samme måde.

Cipher block chaining (CBC)Rediger

CBC

Cipher block chaining

Kryptering kan paralleliseres

Nej

Dekryptering kan paralleliseres

Ja

Random læseadgang

Ja

Ehrsam, Meyer, Smith og Tuchman opfandt CBC-driftsformen (cipher block chaining) i 1976. I CBC-tilstand XOR’er hver blok af klartekst med den foregående ciphertextblok, inden den krypteres. På denne måde afhænger hver enkelt krypteringstekstblok af alle de klartekstblokke, der er behandlet indtil da. For at gøre hver meddelelse unik skal der anvendes en initialiseringsvektor i den første blok.

Hvis den første blok har indeks 1, er den matematiske formel for CBC-kryptering

C i = E K ( P i ⊕ C i – 1 ) , {{\displaystyle C_{i}=E_{K}(P_{i}\oplus C_{i-1}),}

C 0 = I V , {\displaystyle C_{0}=IV,}

men den matematiske formel for CBC-dekryptering er

P i = D K ( C i ) ⊕ C i – 1 , {\displaystyle P_{i}=D_{K}(C_{i})\oplus C_{i-1},}

C 0 = I V . {\displaystyle C_{0}=IV.}

EksempelRediger

CBC har været den mest almindeligt anvendte funktionsmåde. Dens største ulemper er, at krypteringen er sekventiel (dvs. den kan ikke paralleliseres), og at meddelelsen skal fyldes op til et multiplum af krypteringsblokkens størrelse. En måde at håndtere dette sidste problem på er ved hjælp af en metode, der er kendt som ciphertext stealing. Bemærk, at en ændring på én bit i en klartekst eller initialiseringsvektor (IV) påvirker alle følgende ciffertekstblokke.

Dekryptering med den forkerte IV medfører, at den første blok af klartekst er korrupt, men at efterfølgende klartekstblokke vil være korrekte. Dette skyldes, at hver blok er XORed med cipherteksten for den foregående blok, ikke klarteksten, så man behøver ikke at dekryptere den foregående blok, før man bruger den som IV for dekrypteringen af den aktuelle blok. Det betyder, at en klartekstblok kan genfindes fra to tilstødende blokke af ciffertekst. Som følge heraf kan dekrypteringen paralleliseres. Det skal bemærkes, at en ændring på én bit i cifferteksten medfører fuldstændig ødelæggelse af den tilsvarende blok af klartekst og inverterer den tilsvarende bit i den efterfølgende blok af klartekst, men resten af blokkene forbliver intakte. Denne ejendommelighed udnyttes i forskellige padding oracle-angreb, som f.eks. POODLE.

Explicit initialization vectors udnytter denne egenskab ved at tilføje en enkelt tilfældig blok til klarteksten. Krypteringen foregår som normalt, bortset fra at IV’en ikke behøver at blive kommunikeret til dekrypteringsrutinen. Uanset hvilken IV dekrypteringen anvender, er det kun den tilfældige blok, der “ødelægges”. Den kan trygt kasseres, og resten af dekrypteringen er den oprindelige klartekst.

Propagating cipher block chaining (PCBC)Rediger

PCBC

Propagating cipher block chaining

Kryptering paralleliserbar

Nej

Dekryptering paralleliserbar

Nej

Random read access

Nej

Den propagating cipher block chaining eller plaintext cipher-block chaining-tilstand blev designet til at få små ændringer i cipherteksten til at forplante sig i det uendelige ved dekryptering, såvel som ved kryptering. I PCBC-tilstand XOR-ordnes hver blok af klartekst med både den foregående blok af klartekst og den foregående blok af ciffertekst, inden den krypteres. Ligesom ved CBC-tilstand anvendes en initialiseringsvektor i den første blok.

Krypterings- og dekrypteringsalgoritmerne er som følger:

C i = E K ( P i ⊕ P i ⊕ P i – 1 ⊕ C i – 1 ) , P 0 ⊕ C 0 = I V , {\displaystyle C_{i}=E_{K}(P_{i}\oplus P_{i-1}\oplus C_{i-1}),P_{0}\oplus C_{0}=IV,}

P i = D K ( C i ) ⊕ P i – 1 ⊕ C i – 1 , P 0 ⊕ C 0 = I V . {\displaystyle P_{i}=D_{K}(C_{i})\oplus P_{i-1}\oplus C_{i-1},P_{0}\oplus C_{0}=IV.}

PCBC anvendes især i Kerberos v4 og WASTE, men er ellers ikke almindelig. På en meddelelse, der er krypteret i PCBC-tilstand, påvirker det ikke dekrypteringen af efterfølgende blokke, hvis to tilstødende ciphertext-blokke udveksles, hvis dette ikke påvirker dekrypteringen af efterfølgende blokke. Af denne grund anvendes PCBC ikke i Kerberos v5.

Cipher feedback (CFB)Rediger

Fuld-blok CFBEdit

CFB

Cipher feedback

Kryptering kan paralleliseres

Nej

Dekryptering paralleliserbar

Ja

Random read access

Ja

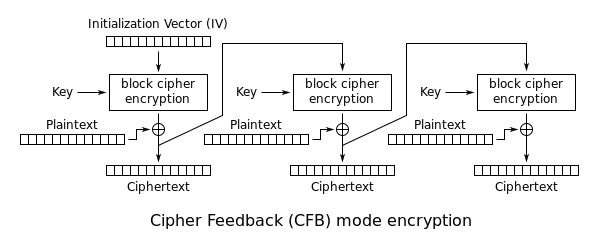
Cipher feedback (CFB)-tilstand (cipher feedback), bruger i sin enkleste form hele blokchifferens output. I denne variant, der minder meget om CBC, gør den en blokchiffer til en selvsynkroniserende stream cipher. CFB-dekryptering i denne variant er næsten identisk med CBC-kryptering udført i omvendt rækkefølge:

C i = { IV , i = 0 E K ( C i – 1 ) ⊕ P i , ellers P i = E K ( C i – 1 ) ⊕ C i , {\displaystyle {\begin{aligned}C_{i}&={\begin{cases}{\text{IV}},&i=0\\E_{K}(C_{i-1})\oplus P_{i},&{\text{otherwise}}\end{cases}}\\P_{i}&=E_{K}(C_{i-1})\oplus C_{i},\end{aligned}}}

CFB-1, CFB-8, CFB-64, CFB-128 osv.Rediger

NIST SP800-38A definerer CFB med en bit-bredde. CFB-tilstanden kræver også en heltalsparameter, betegnet s, således at 1 ≤ s ≤ b. I specifikationen af CFB-tilstanden nedenfor består hvert klartekstsegment (Pj) og ciffertekstsegment (Cj) af s bits. Værdien af s indgår undertiden i navnet på tilstanden, f.eks. 1-bit CFB-tilstand, 8-bit CFB-tilstand, 64-bit CFB-tilstand, 64-bit CFB-tilstand eller 128-bit CFB-tilstand.

Disse tilstande afkorter output af den underliggende blokchiffer.

I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}

I i = ( ( ( I i – 1 ≪ s ) + C i ) mod 2 b , {{\displaystyle I_{i}={\big (}(I_{i-1}\ll s)+C_{i}{\big )}{\bmod {2}}}^{b},}

C i = MSB s ( E K ( I i – 1 ) ) ) ⊕ P i , {\displaystyle C_{i}=\operatornavn {MSB} _{s}{\big (}E_{K}(I_{i-1}){\big )}\oplus P_{i},}

P i = MSB s ( E K ( I i – 1 ) ) ⊕ C i , {\displaystyle P_{i}=\operatornavn {MSB} _{s}{\big (}E_{K}(I_{i-1}){\big )}\oplus C_{i},}

CFB-1 anses for at være selvsynkroniserende og modstandsdygtig over for tab af ciffertekst; “Når 1-bit CFB-tilstanden anvendes, genoprettes synkroniseringen automatisk b+1 positioner efter den indsatte eller slettede bit. For andre værdier af s i CFB-tilstand og for de andre fortrolighedstilstande i denne anbefaling skal synkroniseringen genoprettes eksternt.” (NIST SP800-38A). Dvs. 1-bit tab i en 128-bit bred blokchiffer som AES vil gøre 129 ugyldige bits før der udsendes gyldige bits.

CFB kan også selvsynkronisere i nogle andre specielle tilfælde end dem, der er angivet. F.eks. vil en ændring på én bit i CFB-128 med en underliggende 128-bits blokchiffer blive re-synkroniseret efter to blokke. (CFB-128 osv. vil dog ikke håndtere bittab elegant; et tab på én bit vil medføre, at dekrypteringsenheden mister alignment med krypteringsenheden)

CFB sammenlignet med andre tilstandeRediger

Lige CBC-tilstand forplanter ændringer i klarteksten sig for evigt i krypteringsteksten, og kryptering kan ikke paralleliseres. Ligesom CBC kan dekryptering også paralleliseres.

CFB, OFB og CTR har to fælles fordele i forhold til CBC-tilstand: blokcifringen anvendes altid kun i krypteringsretningen, og meddelelsen behøver ikke at blive polstret til et multiplum af cipherblokstørrelsen (selv om ciphertext stealing også kan anvendes til CBC-tilstand for at gøre polstring unødvendig).

Output feedback (OFB)Rediger

OFB

Output feedback

Kryptering kan paralleliseres

Nej

Dekryptering parallelizable

No

Random read access

No

Den output feedback (OFB)-tilstand gør en block cipher til en synkron stream cipher. Den genererer keystream-blokke, som derefter XOR-opereres med klartekstblokkene for at få den krypterede tekst. Ligesom med andre stream ciphers giver vending af en bit i cipherteksten en vending af en bit i klarteksten på samme sted. Denne egenskab gør det muligt for mange fejlkorrigerende koder at fungere normalt, selv når de anvendes før kryptering.

På grund af symmetrien i XOR-operationen er kryptering og dekryptering nøjagtig ens:

C j = P j ⊕ O j , {\displaystyle C_{j}=P_{j}\oplus O_{j},}

P j = C j ⊕ O j , {\displaystyle P_{j}=C_{j}\oplus O_{j},}

O j = E K ( I j ) , {\displaystyle O_{j}=E_{K}(I_{j}),}

I j = O j – 1 , {\displaystyle I_{j}=O_{j-1},}

I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}

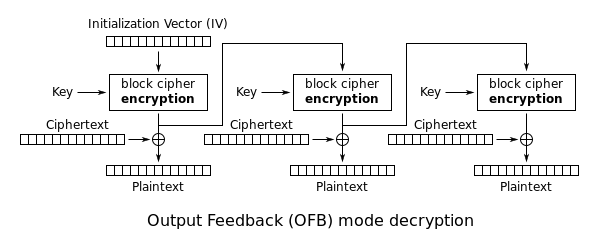
Hver output feedback block cipher operation afhænger af alle de foregående, og kan derfor ikke udføres parallelt. Men da klarteksten eller cipherteksten kun bruges til den endelige XOR, kan blokchifferoperationerne udføres på forhånd, så det sidste trin kan udføres parallelt, når klarteksten eller cipherteksten er tilgængelig.

Det er muligt at opnå en OFB-mode nøglestrøm ved at bruge CBC-mode med en konstant streng af nuller som input. Dette kan være nyttigt, fordi det giver mulighed for at anvende hurtige hardwareimplementeringer af CBC-tilstand til OFB-tilstandskryptering.

Ved anvendelse af OFB-tilstand med en delvis blok som feedback ligesom CFB-tilstand reduceres den gennemsnitlige cykluslængde med en faktor 232 eller mere. En matematisk model foreslået af Davies og Parkin og underbygget af eksperimentelle resultater viste, at kun med fuld feedback kan der opnås en gennemsnitlig cykluslængde tæt på det opnåelige maksimum. Af denne grund blev støtte til afkortet feedback fjernet fra OFB-specifikationen.

Counter (CTR)Edit

CTR

Counter

Kryptering paralleliserbar

Ja

Dekryptering paralleliserbar

Ja

Random læseadgang

Ja

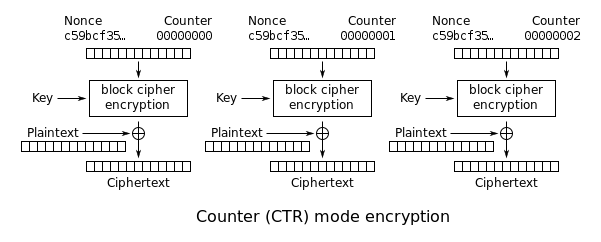
Note: CTR-tilstand (CM) er også kendt som ICM-tilstand (integer counter mode) og SIC-tilstand (segmented integer counter).

Lige OFB forvandler counter mode en block cipher til en stream cipher. Den genererer den næste nøglestrømblok ved at kryptere på hinanden følgende værdier af en “tæller”. Tælleren kan være en hvilken som helst funktion, der producerer en sekvens, som garanteres ikke at gentage sig i lang tid, selv om en egentlig inkrement-for-en-tæller er den enkleste og mest populære. Brugen af en simpel deterministisk inputfunktion var tidligere kontroversiel; kritikere hævdede, at “bevidst udsættelse af et kryptosystem for et kendt systematisk input udgør en unødvendig risiko”. I dag er CTR-tilstand imidlertid bredt accepteret, og eventuelle problemer betragtes som en svaghed ved den underliggende blokchiffer, som forventes at være sikker uanset systematisk skævhed i dens input. Sammen med CBC er CTR-tilstand en af de to blokchiffertilstande, der anbefales af Niels Ferguson og Bruce Schneier.

CTR-tilstand blev introduceret af Whitfield Diffie og Martin Hellman i 1979.

CTR-tilstand har lignende egenskaber som OFB, men tillader også en egenskab med tilfældig adgang under dekryptering. CTR-tilstand er velegnet til at fungere på en maskine med flere processorer, hvor blokke kan krypteres parallelt. Desuden lider den ikke af det kortcyklusproblem, der kan påvirke OFB.

Hvis IV/nonce er tilfældig, kan de kombineres sammen med tælleren ved hjælp af en hvilken som helst inverterbar operation (sammenkædning, addition eller XOR) for at fremstille den egentlige unikke tællerblok til kryptering. Hvis der er tale om en ikke-tilfældig nonce (f.eks. en pakketæller), skal nonce og tæller sammenkædes (f.eks. ved at lagre nonce i de øverste 64 bit og tælleren i de nederste 64 bit i en 128-bit tællerblok). Hvis nonce og tæller blot adderes eller XOR-eserveres til en enkelt værdi, vil det i mange tilfælde bryde sikkerheden i forbindelse med et angreb med valgt tekst i mange tilfælde, da angriberen kan være i stand til at manipulere hele IV-tællerparret for at forårsage en kollision. Når en angriber først kontrollerer IV-tællerparret og klarteksten, vil XOR af cifferteksten med den kendte klartekst give en værdi, der, når den XOR’er med cifferteksten i den anden blok, der deler det samme IV-tællerpar, vil dekryptere den pågældende blok.

Bemærk, at nonce i dette diagram svarer til initialiseringsvektoren (IV) i de andre diagrammer. Hvis offset/lokaliseringsoplysningerne er korrupte, vil det imidlertid være umuligt at genoprette sådanne data delvist på grund af afhængigheden af byteoffset.