Tri de sélection – Algorithme, code source, complexité temporelle

Cet article fait partie de la série « Algorithmes de tri : Ultimate Guide » et…

• décrit le fonctionnement du Tri de sélection,
• inclut le code source Java du Tri de sélection,
• montre comment dériver sa complexité temporelle (sans mathématiques compliquées)
• et vérifie si les performances de l’implémentation Java correspondent au comportement d’exécution attendu.

Vous pouvez trouver le code source de toute la série d’articles dans mon dépôt GitHub.

Exemple : Trier des cartes à jouer

Trier des cartes à jouer dans la main est l’exemple classique du tri par insertion.

Le tri par sélection peut également être illustré avec des cartes à jouer. Je ne connais personne qui ramasse ses cartes de cette façon, mais à titre d’exemple, cela fonctionne plutôt bien 😉

D’abord, vous posez toutes vos cartes face visible sur la table devant vous. Vous cherchez la carte la plus petite et vous la prenez à gauche de votre main. Ensuite, vous cherchez la carte suivante plus grande et vous la placez à droite de la plus petite carte, et ainsi de suite jusqu’à ce que vous preniez finalement la plus grande carte à l’extrême droite.

Différence avec le tri par insertion

Avec le tri par insertion, nous prenons la carte suivante non triée et nous l’insérons à la bonne position dans les cartes triées.

Le tri par sélection fonctionne en quelque sorte à l’inverse : Nous sélectionnons la plus petite carte parmi les cartes non triées et ensuite – l’une après l’autre – nous l’ajoutons aux cartes déjà triées.

Algorithme de tri par sélection

L’algorithme peut être expliqué le plus simplement par un exemple. Dans les étapes suivantes, je montre comment trier le tableau avec le tri par sélection :

Etape 1

Nous divisons le tableau en une partie gauche, triée, et une partie droite, non triée. La partie triée est vide au départ:

Étape 2

Nous recherchons le plus petit élément dans la partie droite, non triée. Pour ce faire, nous nous souvenons d’abord du premier élément, qui est le 6. Nous passons à la zone suivante, où nous trouvons un élément encore plus petit dans le 2. Nous parcourons le reste du tableau, à la recherche d’un élément encore plus petit. Comme nous n’en trouvons pas, nous nous en tenons au 2. Nous le plaçons à la bonne place en l’échangeant avec l’élément qui se trouve à la première place. Puis nous déplaçons la frontière entre les sections du tableau d’un champ vers la droite:

Étape 3

Nous cherchons à nouveau dans la partie droite, non triée, le plus petit élément. Cette fois, c’est le 3 ; nous le permutons avec l’élément en deuxième position :

Étape 4

Nous cherchons à nouveau le plus petit élément dans la partie droite. C’est le 4, qui est déjà dans la bonne position. Il n’y a donc pas besoin d’opération de permutation dans cette étape, et nous déplaçons simplement la bordure de la section :

Étape 5

Comme plus petit élément, nous trouvons le 6. Nous le permutons avec l’élément au début de la partie droite, le 9:

Étape 6

Des deux éléments restants, le 7 est le plus petit. Nous l’échangeons avec le 9:

Algorithme terminé

Le dernier élément est automatiquement le plus grand et, par conséquent, dans la bonne position. L’algorithme est terminé, et les éléments sont triés :

Code source Java du tri par sélection

Dans cette section, vous trouverez une implémentation Java simple du tri par sélection.

La boucle externe itère sur les éléments à trier, et elle se termine après l’avant-dernier élément. Lorsque cet élément est trié, le dernier élément est automatiquement trié lui aussi. La variable de boucle i pointe toujours vers le premier élément de la partie droite, non triée.

Dans chaque cycle de boucle, le premier élément de la partie droite est initialement supposé être le plus petit élément min ; sa position est stockée dans minPos.

La boucle interne itère ensuite du deuxième élément de la partie droite à sa fin et réaffecte min et minPos chaque fois qu’un élément encore plus petit est trouvé.

Une fois la boucle interne terminée, les éléments des positions i (début de la partie droite) et minPos sont permutés (sauf s’il s’agit du même élément).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

Le code présenté diffère de la classe SelectionSort dans le dépôt GitHub en ce qu’il implémente l’interface SortAlgorithm pour être facilement interchangeable dans le cadre de test.

Complexité temporelle du tri de sélection

Nous désignons par n le nombre d’éléments, dans notre exemple n = 6.

Les deux boucles imbriquées sont une indication que nous avons affaire à une complexité temporelle* de O(n²). Ce sera le cas si les deux boucles itèrent vers une valeur qui augmente linéairement avec n.

C’est évidemment le cas de la boucle extérieure : elle compte jusqu’à n-1.

Qu’en est-il de la boucle interne ?

Regardez l’illustration suivante :

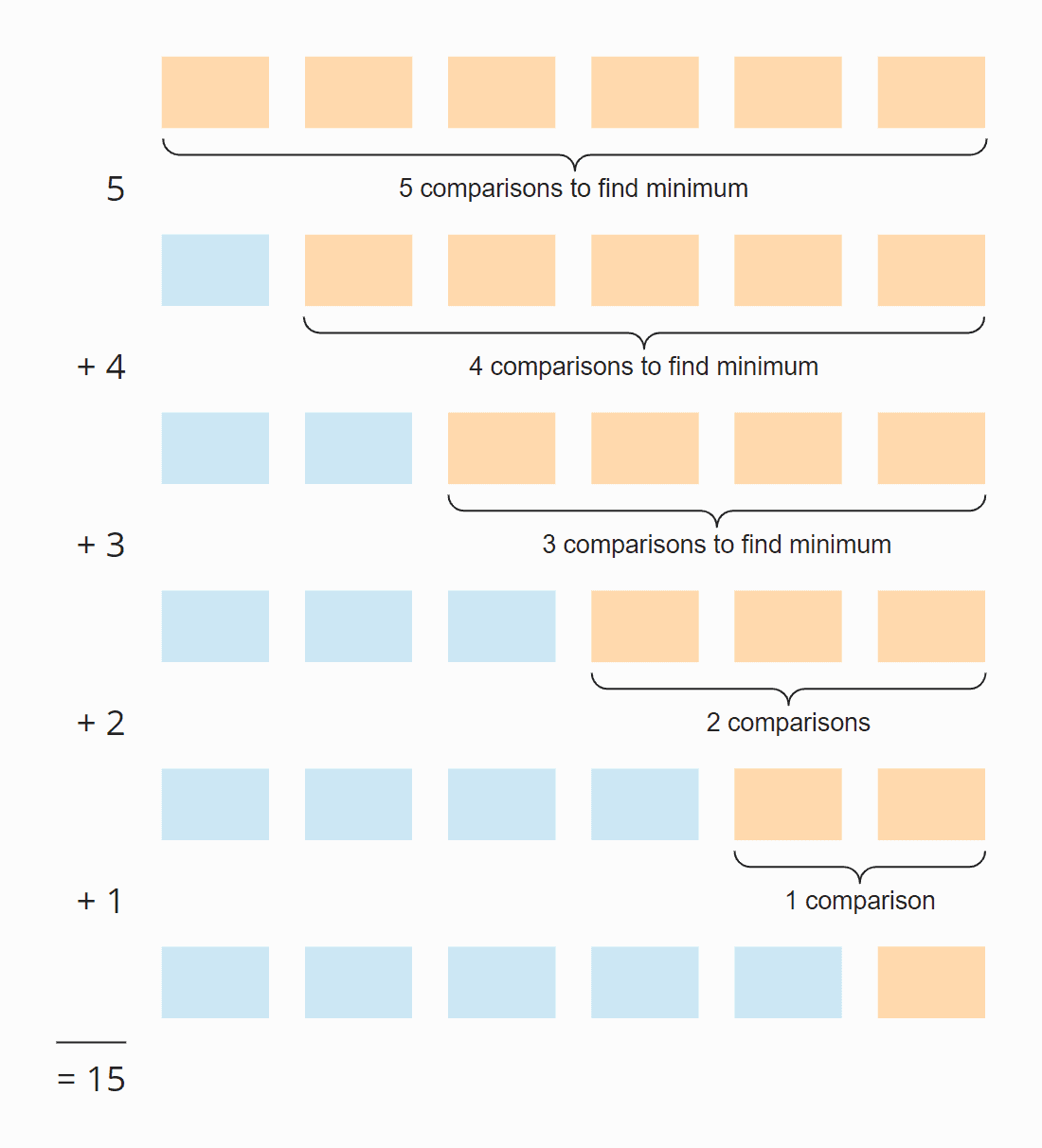
À chaque étape, le nombre de comparaisons est inférieur d’une unité au nombre d’éléments non triés. Au total, il y a 15 comparaisons – que le tableau soit initialement trié ou non.

Ce chiffre peut aussi être calculé comme suit :

Six éléments fois cinq étapes ; divisé par deux, puisqu’en moyenne sur toutes les étapes, la moitié des éléments sont encore non triés :

6 × 5 × ½ = 30 × ½ = 15

Si on remplace 6 par n, on obtient

n × (n – 1) × ½

En multipliant, cela donne :

½ n² – ½ n

La plus grande puissance de n dans ce terme est n². La complexité temporelle pour la recherche du plus petit élément est, par conséquent, O(n²) – également appelée « temps quadratique ».

Regardons maintenant la permutation des éléments. A chaque étape (sauf la dernière), un élément est permuté ou aucun, selon que le plus petit élément est déjà à la bonne position ou non. On a donc, en somme, un maximum de n-1 opérations de permutation, soit une complexité temporelle de O(n) – aussi appelée « temps linéaire ».

Pour la complexité totale, seule la classe de complexité la plus élevée compte, donc :

La complexité temporelle moyenne, dans le meilleur des cas et dans le pire des cas du Tri par sélection est de : O(n²)

* Les termes « complexité temporelle » et « O-notation » sont expliqués dans cet article à l’aide d’exemples et de diagrammes.

Runtime de l’exemple Java Selection Sort

Assez de théorie ! J’ai écrit un programme de test qui mesure le temps d’exécution de Selection Sort (et de tous les autres algorithmes de tri traités dans cette série) comme suit :

• Le nombre d’éléments à trier double après chaque itération, depuis initialement 1 024 éléments jusqu’à 536 870 912 (= 229) éléments. Un tableau deux fois plus grand ne peut être créé en Java.
• Si un test prend plus de 20 secondes, le tableau n’est pas étendu davantage.
• Tous les tests sont exécutés avec des éléments non triés ainsi que des éléments pré-triés ascendants et descendants.
• Nous permettons au compilateur HotSpot d’optimiser le code avec deux tours de chauffe. Après cela, les tests sont répétés jusqu’à ce que le processus soit interrompu.

Après chaque itération, le programme imprime la médiane de tous les résultats de mesure précédents.

Voici le résultat pour le tri par sélection après 50 itérations (par souci de clarté, ce n’est qu’un extrait ; le résultat complet peut être trouvé ici) :

n	non trié	ascendant	descendant
…	…	…	…
16,384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Voici les mesures une fois de plus sous forme de diagramme (où j’ai affiché « non trié » et « ascendant » comme une seule courbe en raison des valeurs presque identiques) :

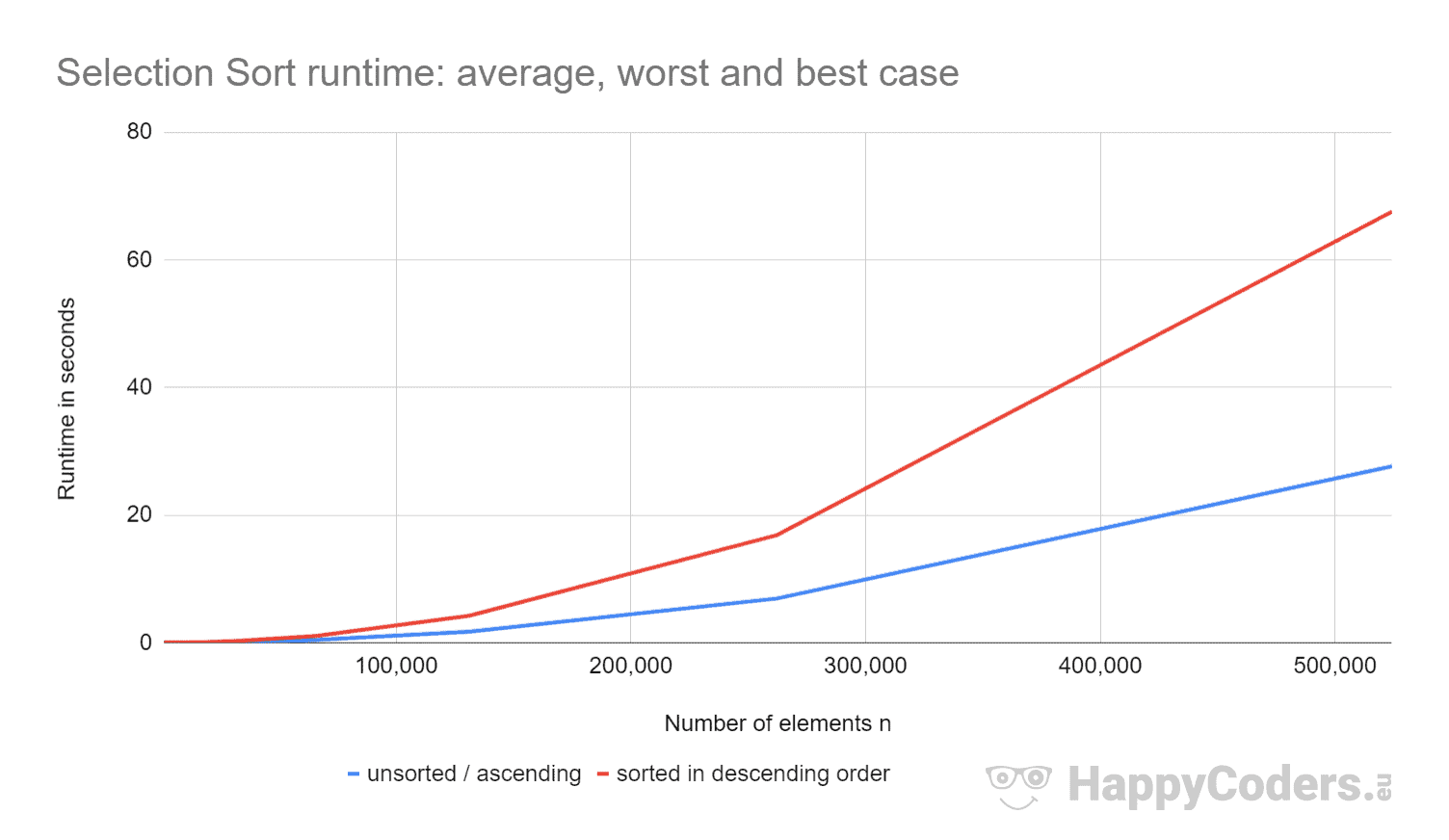
Il est bon de voir que

• si le nombre d’éléments est doublé, le temps d’exécution est approximativement quadruplé – indépendamment du fait que les éléments soient préalablement triés ou non. Cela correspond à la complexité temporelle attendue de O(n²).
• que le temps d’exécution pour les éléments triés ascendants est légèrement meilleur que pour les éléments non triés. Cela est dû au fait que les opérations de permutation, qui – comme analysé ci-dessus – sont de peu d’importance, ne sont pas nécessaires ici.
• que le temps d’exécution pour les éléments triés descendants est significativement pire que pour les éléments non triés.

Pourquoi cela ?

Analyse du temps d’exécution dans le pire des cas

Théoriquement, la recherche du plus petit élément devrait toujours prendre le même temps, quelle que soit la situation initiale. Et les opérations de permutation ne devraient être que légèrement supérieures pour les éléments triés par ordre décroissant (pour les éléments triés par ordre décroissant, chaque élément devrait être permuté ; pour les éléments non triés, presque chaque élément devrait être permuté).

En utilisant le programme CountOperations de mon dépôt GitHub, nous pouvons voir le nombre de diverses opérations. Voici les résultats pour les éléments non triés et les éléments triés par ordre décroissant, résumés dans un seul tableau :

.

n	Comparaisons	Échanges non triés	Échanges décroissants	minPos/min non triés	minPos/min décroissants
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

D’après les valeurs mesurées, on peut constater :

• Avec des éléments triés par ordre décroissant, on a – comme prévu – autant d’opérations de comparaison qu’avec des éléments non triés – soit n × (n-1) / 2.
• Avec des éléments non triés, nous avons – comme supposé – presque autant d’opérations de permutation que d’éléments : par exemple, avec 4 096 éléments non triés, il y a 4 084 opérations de permutation. Ces chiffres changent aléatoirement d’un test à l’autre.
• Toutefois, avec des éléments triés par ordre décroissant, nous avons seulement la moitié d’opérations de swap que d’éléments ! C’est parce que, lors de la permutation, nous ne mettons pas seulement le plus petit élément au bon endroit, mais aussi le partenaire de permutation respectif.

Avec huit éléments, par exemple, nous avons quatre opérations de permutation. Dans les quatre premières itérations, nous en avons une chacune et dans les itérations cinq à huit, aucune (néanmoins l’algorithme continue à fonctionner jusqu’à la fin) :

De plus, nous pouvons lire dans les mesures :

• La raison pour laquelle le tri par sélection est tellement plus lent avec des éléments triés par ordre décroissant peut être trouvée dans le nombre d’affectations de variables locales (minPos et min) lors de la recherche du plus petit élément. Alors qu’avec 8 192 éléments non triés, nous avons 69 378 de ces affectations, avec des éléments triés par ordre décroissant, il y a 16 785 407 de ces affectations – c’est 242 fois plus !

Pourquoi cette énorme différence ?

Analyse du temps d’exécution de la recherche du plus petit élément

Pour les éléments triés par ordre décroissant, l’ordre de grandeur peut être dérivé de l’illustration juste au-dessus. La recherche du plus petit élément se limite au triangle des cases orange et orange-bleu. Dans la partie supérieure orange, les chiffres de chaque case deviennent plus petits ; dans la partie droite orange-bleu, les chiffres augmentent à nouveau.

Des opérations d’affectation ont lieu dans chaque case orange et dans la première des cases orange-bleu. Le nombre d’opérations d’affectation pour minPos et min est donc, au sens figuré, d’environ « un quart de carré » – mathématiquement et précisément, c’est ¼ n² + n – 1.

Pour les éléments non triés, il faudrait pénétrer beaucoup plus profondément dans la matière. Cela dépasserait non seulement le cadre de cet article, mais de tout le blog.

C’est pourquoi je limite mon analyse à un petit programme de démonstration qui mesure le nombre d’affectations minPos/min lors de la recherche du plus petit élément dans un tableau non trié. Voici les valeurs moyennes après 100 itérations (un petit extrait ; les résultats complets peuvent être trouvés ici):

n	nombre moyen d’affectations minPos/min
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Voici un diagramme avec axe des x logarithmique:

Le diagramme montre très bien que nous avons une croissance logarithmique, c’est-à-dire, à chaque fois que l’on double le nombre d’éléments, le nombre d’affectations n’augmente que d’une valeur constante. Comme je l’ai dit, je n’irai pas plus loin dans les antécédents mathématiques.

C’est la raison pour laquelle ces minPos/min assignations ont peu d’importance dans les tableaux non triés.

Autres caractéristiques du tri sélectif

Dans les sections suivantes, j’aborderai la complexité spatiale, la stabilité et la parallélisabilité du tri sélectif.

Complexité spatiale du tri sélectif

La complexité spatiale du tri sélectif est constante puisque nous n’avons pas besoin d’espace mémoire supplémentaire en dehors des variables de boucle i et j et des variables auxiliaires length, minPos et min.

C’est-à-dire que quel que soit le nombre d’éléments que nous trions – dix ou dix millions – nous n’avons jamais besoin que de ces cinq variables supplémentaires. On note le temps constant comme O(1).

Stabilité du tri sélectif

Le tri sélectif semble stable à première vue : Si la partie non triée contient plusieurs éléments avec la même clé, les premiers doivent être annexés à la partie triée en premier.

Mais les apparences sont trompeuses. Car en permutant deux éléments dans la deuxième sous-étape de l’algorithme, il peut arriver que certains éléments de la partie non triée n’aient plus l’ordre initial. Ce qui, à son tour, conduit au fait qu’ils n’apparaissent plus dans l’ordre original dans la partie triée.

Un exemple peut être construit très simplement. Supposons que nous ayons deux éléments différents avec la clé 2 et un avec la clé 1, disposés comme suit, et que nous les triions ensuite avec Selection Sort:

Dans la première étape, le premier et le dernier élément sont permutés. Ainsi, l’élément « TWO » se retrouve derrière l’élément « two » – l’ordre des deux éléments est permuté.

Dans la deuxième étape, l’algorithme compare les deux éléments arrière. Tous deux ont la même clé, 2. Aucun élément n’est donc permuté.

A la troisième étape, il ne reste qu’un seul élément ; celui-ci est automatiquement considéré comme trié.

Les deux éléments avec la clé 2 ont donc été permutés dans leur ordre initial – l’algorithme est instable.

Variante stable du tri par sélection

Le tri par sélection peut être rendu stable en ne permutant pas le plus petit élément avec le premier à l’étape deux, mais en décalant tous les éléments entre le premier et le plus petit élément d’une position vers la droite et en insérant le plus petit élément au début.

Même si la complexité temporelle restera la même en raison de ce changement, les décalages supplémentaires entraîneront une dégradation significative des performances, au moins lorsque nous trions un tableau.

Avec une liste chaînée, couper et coller l’élément à trier pourrait être fait sans perte de performance significative.

Parallélisabilité du tri par sélection

Nous ne pouvons pas paralléliser la boucle externe car elle change le contenu du tableau à chaque itération.

La boucle interne (recherche du plus petit élément) peut être parallélisée en divisant le tableau, en recherchant le plus petit élément dans chaque sous-réseau en parallèle, et en fusionnant les résultats intermédiaires.

Tri par sélection vs Tri par insertion

Quel algorithme est le plus rapide, le Tri par sélection ou le Tri par insertion ?

Comparons les mesures de mes implémentations Java.

Je laisse de côté le meilleur cas. Avec Insertion Sort, la complexité temporelle dans le meilleur des cas est O(n) et a pris moins d’une milliseconde pour un maximum de 524 288 éléments. Donc, dans le meilleur des cas, Insertion Sort est, pour n’importe quel nombre d’éléments, des ordres de grandeur plus rapide que Selection Sort.

n	Tri de sélection non trié	Tri d’insertion non trié	Tri de sélection descendant	Tri d’insertion descendant
…	…	…	…	…
16,384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65,536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46,309,3 ms

Et encore une fois sous forme de diagramme:

Le tri par insertion est, par conséquent, non seulement plus rapide que le tri par sélection dans le meilleur des cas, mais aussi dans le cas moyen et le pire des cas.

La raison en est que le tri par insertion nécessite, en moyenne, deux fois moins de comparaisons. Pour rappel, avec le Tri par insertion, nous avons des comparaisons et des décalages moyennant jusqu’à la moitié des éléments triés ; avec le Tri par sélection, nous devons rechercher le plus petit élément dans tous les éléments non triés à chaque étape.

Le Tri par sélection a nettement moins d’opérations d’écriture, donc le Tri par sélection peut être plus rapide lorsque les opérations d’écriture sont coûteuses. Ce n’est pas le cas avec les écritures séquentielles dans les tableaux, car celles-ci sont principalement effectuées dans le cache du CPU.

En pratique, le Tri de sélection n’est, par conséquent, presque jamais utilisé.

Résumé

Le Tri de sélection est un algorithme de tri facile à mettre en œuvre, et dans son implémentation typique instable, avec une complexité temporelle moyenne, dans le meilleur des cas et dans le pire des cas de O(n²).

Le tri par sélection est plus lent que le tri par insertion, c’est pourquoi il est rarement utilisé en pratique.

Vous trouverez d’autres algorithmes de tri dans cet aperçu de tous les algorithmes de tri et de leurs caractéristiques dans la première partie de la série d’articles.

Si vous avez aimé cet article, n’hésitez pas à le partager en utilisant l’un des boutons de partage à la fin. Vous souhaitez être informé par email lorsque je publie un nouvel article ? Alors utilisez le formulaire suivant pour vous inscrire à ma newsletter.

.