Quelles sont les fréquences des notes de musique ?

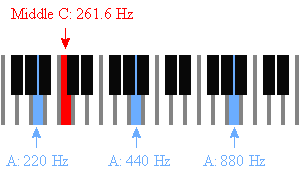
Tableau des fréquences musicales

On les trouve en utilisant

la fréquence `= 440×2^(n »/ »12)`

pour `n = -21, -19, …., 27`

D’où vient cette formule ?

Ce problème m’a rappelé l’intérêt composé que nous avons rencontré plus tôt dans les mathématiques monétaires. La fréquence doit doubler toutes les `12` notes (parce qu’il y a `7` notes blanches et `5` notes noires dans chaque octave.)

Voici un graphique de cette relation :

fréquence `= 440×2^(n »/ »12)`

C’est une courbe exponentielle, que nous avons rencontrée plus tôt dans Graphes des fonctions exponentielles.

Accord tempéré égal

Un problème intéressant se pose aux fabricants d’instruments de musique depuis des centaines d’années. Pour obtenir une « quinte parfaite » (l’intervalle entre le la et le mi ci-dessus, disons), nous devons jouer une note qui a `1,5` fois la fréquence du la.

Sur un violon (ou un alto ou tout instrument à cordes sans frettes), c’est possible, et nous pouvons jouer un beau mi parfait à `440 × 1,5 = 660 `Hz`. Mais remarquez (d’après le tableau de fréquences ci-dessus) qu’un piano jouant la même note jouera un mi `= 659,26\ »Hz »` .

Il y a environ 400 ans, les claviers (généralement les clavecins et les orgues) étaient accordés pour un groupe particulier de touches, afin que tous les instruments, en particulier les cordes, sonnent « juste » dans ces touches. Le clavecin sonnait très bien dans ces tonalités, mais assez terriblement dans d’autres tonalités sans rapport (disons le si bémol).

Il y avait en fait plusieurs systèmes d’accordage différents en usage à l’époque de Bach, dont le meantone (qui visait à faire bien sonner les tierces majeures, mais ne se préoccupait pas autant de la qualité des quintes majeures, avec pour effet que certaines tonalités n’étaient pas utilisables), et l’accordage de 1691 de Werckmeister qui permettait aux compositeurs de créer de la musique dans n’importe quelle tonalité (avec pour effet que les différentes tonalités avaient une qualité tonale différente).

Au début du 20ème siècle, il a été décidé d’accorder les claviers de façon à ce que les notes soient régulièrement espacées (comme les fréquences données dans le tableau présenté ci-dessus). C’est ce qu’on appelle l’accordage à tempérament égal. Un tel accordage était connu à l’époque de Bach, mais rejeté parce qu’il était considéré comme trop « fade » (toutes les touches ont la même qualité de son) et qu’il n’existait pas d’outils de mesure des fréquences qui auraient permis des accords exacts.

Malheureusement, l’accordage tempéré égal signifie que tous les instruments à cordes doivent tenir compte des légères différences d’accordage entre les instruments lorsque les claviers sont également concernés. Les cordes sont généralement plus heureuses lorsqu’elles jouent uniquement avec d’autres cordes, pour cette raison.