
Rośliny mogą rosnąć nowe komórki w spiralach, takich jak wzór nasion w tym pięknym słoneczniku.
Spirala dzieje się naturalnie, ponieważ każda nowa komórka powstaje po obrocie.
„Nowa komórka, potem obrót,
tam kolejna komórka, potem obrót, …”
Jak daleko obrócić?
Więc, gdybyś był rośliną, ile skrętu miałbyś pomiędzy nowymi komórkami?
Jeśli nie skręcisz w ogóle, otrzymasz linię prostą.
![]()
Ale to jest bardzo kiepski projekt …. chcesz coś okrągłego, co będzie trzymać się razem bez szczelin.
Dlaczego nie spróbować znaleźć najlepszą wartość dla siebie?
Spróbuj różnych wartości, takich jak 0,75, 0,9, 3,1416, 0,62, itp.
Pamiętaj, próbujesz zrobić wzór bez przerw od początku do końca:
(Przy okazji, to nie ma znaczenia o całej części liczby, jak 1. lub 5. ponieważ są to pełne obroty, które wskazują nam z powrotem w tym samym kierunku.)
What Did You Get?
Jeśli masz coś, co kończy się jak 0.618 (lub 0.382, co jest 1 – 0.618) wtedy „Gratulacje, jesteś udanym członkiem królestwa roślin!”
 |
To dlatego, że Złoty Stosunek (1.61803…) jest najlepszym rozwiązaniem, a Słonecznik odkrył to na swój własny, naturalny sposób. Spróbuj… powinno to wyglądać tak. |
Dlaczego?
Każda liczba, która jest ułamkiem zwykłym (przykład: 0.75 to 3/4, a 0,95 to 19/20, itd.) po pewnym czasie tworzy wzór linii układających się w stos, co powoduje powstanie luk.
Ale Złota Proporcja (jej symbolem jest grecka litera Phi, pokazana po lewej) jest ekspertem w niebyciu żadnym ułamkiem.
Jest to liczba irracjonalna (co oznacza, że nie możemy jej zapisać jako ułamek zwykły), ale co więcej… jest tak daleka od bycia jakimkolwiek ułamkiem, jak to tylko możliwe.
| Samo bycie irracjonalną nie wystarczy | |
|---|---|
 |
Pi (3.141592654…), która również jest irracjonalna. Niestety ma ona zapis dziesiętny bardzo bliski 1/7 (= 0,142857…), więc kończy się na 7 ramionach. |
 |
e (2,71828….) również irracjonalne, nie działa również, ponieważ jego ułamek dziesiętny jest bliski 5/7 (0.714285…), więc również kończy się na 7 ramionach. |
Więc, jak działa złoty stosunek?
| Jedną ze szczególnych właściwości złotego podziału jest to, że można go zdefiniować w odniesieniu do samego siebie, w ten sposób: | |
| (W liczbach: 1,61803… = 1 + 1/1,61803….) | |
| To można rozszerzyć do tego ułamka, który trwa wiecznie (zwanego „ułamkiem ciągłym”): | |
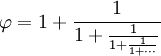 |
|
Tak więc zgrabnie wślizguje się między ułamki zwykłe.
Liczby Fibonacciego
Istnieje specjalny związek pomiędzy Złotym Ratio a Liczbami Fibonacciego (0, 1, 1, 2, 3, 5, 8, 13, 21, … itd, każda liczba jest sumą dwóch liczb przed nią).
Gdy weźmiemy jakiekolwiek dwie kolejne (jedna po drugiej) Liczby Fibonacciego, ich stosunek jest bardzo bliski Złotemu Współczynnikowi:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Więc, tak jak naturalnie otrzymujemy siedem ramion, gdy używamy 0.142857 (1/7), mamy tendencję do otrzymywania liczb Fibonacciego, gdy używamy Złotego Stosunku.
Spróbuj policzyć ramiona spirali – spirale „skręcające w lewo”, a następnie spirale „skręcające w prawo” … jakie liczby otrzymałeś?
Spiralny wzrost liści

To interesujące zachowanie występuje nie tylko w nasionach słonecznika.
Liście, gałęzie i płatki mogą również rosnąć spiralnie.
Dlaczego? Aby nowe liście nie blokowały słońca starszym liściom, lub aby maksymalna ilość deszczu lub rosy została skierowana w dół do korzeni.
W rzeczywistości, kiedy roślina ma spirale, obrót ma tendencję do bycia ułamkiem wykonanym z dwóch kolejnych (jedna po drugiej) liczb Fibonacciego, na przykład:
- Połowa obrotu to 1/2 (1 i 2 są liczbami Fibonacciego)
- 3/5 jest również powszechne (obie liczby Fibonacciego), a
- 5/8 również (zgadłeś!).)
wszystko coraz bliżej Złotej Proporcji.
|
I dlatego Liczby Fibonacciego są bardzo powszechne w roślinach. Tutaj jest stokrotka z 21 płatkami |
 |
Ale nie widzimy tego u wszystkich roślin, ponieważ natura ma wiele różnych metod przetrwania.
Kąt złoty
Do tej pory mówiliśmy o „obrotach” (pełnych rotacjach).
Równowartość 0,61803… obrotów to 222,4922… stopni, czyli około 222,5°.
W drugim kierunku jest to około 137,5°, zwany „Złotym Kątem”.
Więc, następnym razem, gdy będziesz spacerował po ogrodzie, poszukaj Złotego Kąta,
i policz płatki i liście, aby znaleźć Liczby Fibonacciego,
i odkryj jak mądre są rośliny … !
Ćwiczenie
Dlaczego nie pójdziesz teraz do ogrodu lub parku i nie zaczniesz liczyć liści i płatków oraz mierzyć obroty, aby zobaczyć, co znajdziesz.
Możesz zapisać swoje wyniki na tym formularzu:
| Nazwa rośliny lub opis: | ||
| Czy liście rosną spiralnie? T / N | ||
| Oblicz grupę liści: | ||
| Ile pełnych obrotów (b)? | ||
| Obrót na listek (b/a) : | ||
| Kąt obrotu (360 × b/a) : | ||
| Are There Flowers? | ||
(Ale pamiętaj, natura ma swoje własne zasady i nie musi podążać za matematycznymi wzorami,
ale kiedy to robi, jest to niesamowite do zobaczenia.)
* Uwagi o animacji
Ziarna słonecznika rosną od środka na zewnątrz, ale w animacji uznałem, że łatwiej będzie narysować najpierw młodsze ziarna, a potem dodać starsze.
Animacja powinna trwać dłużej, aby była taka sama jak słonecznik – dałoby to w rezultacie 55 spirali zgodnie z ruchem wskazówek zegara i 34 spirale przeciwnie do ruchu wskazówek zegara (kolejne Liczby Fibonacciego). Po prostu nie chciałem, żeby trwało to zbyt długo.
Spirale nie są w nią zaprogramowane – pojawiają się naturalnie w wyniku próby umieszczenia nasion jak najbliżej siebie przy jednoczesnym utrzymaniu ich w prawidłowym obrocie.
.

