
Planten kunnen nieuwe cellen laten groeien in spiralen, zoals het patroon van zaden in deze prachtige zonnebloem.
De spiraal ontstaat op natuurlijke wijze omdat elke nieuwe cel wordt gevormd na een draaiing.
“Nieuwe cel, dan draaien,
dan weer een cel, dan draaien, …”
Hoe ver te draaien?
Als je een plant was, hoe ver moet je dan draaien tussen de nieuwe cellen?
Als je helemaal niet draait, krijg je een rechte lijn.
![]()
Maar dat is een heel slecht ontwerp …. je wilt iets ronds dat zonder spleten in elkaar blijft zitten.
Waarom probeer je niet zelf de beste waarde te vinden?
Probeer verschillende waarden, zoals 0,75, 0,9, 3,1416, 0,62, enz.
Bedenk dat je een patroon probeert te maken zonder tussenruimtes van begin tot eind:
(Overigens maakt het hele getaldeel niet uit, zoals 1. of 5. omdat het volledige omwentelingen zijn die ons weer in dezelfde richting wijzen.)
Wat heb je gekregen?
Als je iets hebt gekregen dat eindigt als 0,618 (of 0,382, wat 1 – 0,618 is) dan “Gefeliciteerd, je bent een succesvol lid van het plantenrijk!”
 |
Dat komt omdat de Gulden Snede verhouding (1.61803…) de beste oplossing is, en de Zonnebloem is daar op zijn eigen natuurlijke manier achter gekomen. Probeer het maar eens… het zou er zo uit moeten zien. |
Waarom?
Elk getal dat een eenvoudige breuk is (voorbeeld: 0.75 is 3/4, en 0,95 is 19/20, enz.) zal na verloop van tijd een patroon maken van lijnen die zich opstapelen, waardoor hiaten ontstaan.
Maar de Gulden Snede (het symbool ervan is de Griekse letter Phi, links afgebeeld) is een expert in het niet zijn van een breuk.
Het is een irrationeel getal (wat betekent dat we het niet kunnen schrijven als een eenvoudige breuk), maar meer dan dat … het is zo ver als we kunnen komen van het zijn van een breuk.
| Alleen irrationeel zijn is niet genoeg | |
|---|---|
 |
Pi (3,141592654…), dat ook irrationeel is. Ongelukkigerwijs heeft het een decimaal die heel dicht bij 1/7 ligt (= 0,142857…), dus komt het uit op 7 armen. |
 |
e (2,71828…) ook irrationeel, werkt ook niet omdat zijn decimaal dicht bij 5/7 ligt (0,714285…), dus komt het ook uit op 7 armen. |
Dus, hoe werkt de Gulden Snede verhouding?
| Een van de bijzondere eigenschappen van de Gulden Snede is dat deze kan worden gedefinieerd in termen van zichzelf, zoals dit: | |
| (In getallen: 1,61803… = 1 + 1/1,61803….) | |
| Dat kan worden uitgebreid tot deze breuk die eeuwig doorgaat (een “doorlopende breuk” genoemd): | |
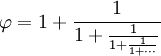 |
|
Dus, het glijdt netjes tussen eenvoudige breuken in.
Fibonacci Getallen
Er is een speciale relatie tussen de Gulden Snede en Fibonacci Getallen (0, 1, 1, 2, 3, 5, 8, 13, 21, … etc, elk getal is de som van de twee getallen ervoor).
Wanneer we twee opeenvolgende (de een na de ander) Fibonacci Getallen nemen, ligt hun verhouding heel dicht bij de Gulden Snede:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Zo, net zoals we natuurlijk zeven armen krijgen als we 0.142857 (1/7), krijgen we van nature Fibonacci-getallen als we de Gulden Snede gebruiken.
Probeer eens de spiraalarmen te tellen – de “linksdraaiende” spiralen, en dan de “rechtsdraaiende” spiralen … welke getallen heb je gekregen?
Spiraalvormige bladgroei

Dit interessante gedrag komt niet alleen voor in zonnebloempitten.
Bladeren, takken en bloemblaadjes kunnen ook spiraalvormig groeien.
Waarom? Zodat nieuwe bladeren de zon niet blokkeren voor oudere bladeren, of zodat de maximale hoeveelheid regen of dauw naar de wortels wordt geleid.
In feite, wanneer een plant spiralen heeft, heeft de draaiing de neiging een breuk te zijn gemaakt met twee opeenvolgende (de een na de ander) Fibonacci Getallen, bijvoorbeeld:
- Een halve draaiing is 1/2 (1 en 2 zijn Fibonacci Getallen)
- 3/5 komt ook vaak voor (beide Fibonacci Getallen), en
- 5/8 ook (u raadt het al!)
alles steeds dichter bij de Gulden Snede.
|
En daarom komen Fibonacci Getallen ook veel voor in planten. Hier is een madeliefje met 21 bloemblaadjes |
 |
Maar we zien dit niet bij alle planten, want de natuur heeft veel verschillende overlevingsmethoden.
Gouden hoek
Tot nu toe hebben we het gehad over “draaiingen” (volledige omwentelingen).
Het equivalent van 0,61803… omwentelingen is 222,4922… graden, oftewel ongeveer 222,5°.
In de andere richting is het ongeveer 137,5°, de zogenaamde “Gouden Hoek”.
Dus, de volgende keer als je in de tuin loopt, zoek dan naar de Gouden Hoek,
en tel bloemblaadjes en blaadjes om Fibonacci Getallen te vinden,
en ontdek hoe slim de planten zijn… !
Oefening
Waarom ga je nu niet de tuin of het park in, en begin blaadjes en bloemblaadjes te tellen, en rotaties te meten om te zien wat je vindt.
Je kunt je resultaten op dit formulier noteren:
| Plantennaam of beschrijving: | ||
| Groeien de bladeren in spiralen? J / N | ||
| Tel een groep Bladeren: | ||
| Hoeveel bladeren (a) ? | ||
| Hoeveel volledige omwentelingen (b) ? | ||
| Rotatiehoek (360 × b/a) : | ||
| Zijn er bloemen? J/N | ||
| Hoeveel bloemblaadjes op Bloem 1: | ||
| Bloem 2: | ||
| Bloem 3: | ||
| : | ||
(Maar vergeet niet, de natuur heeft zijn eigen regels, en het hoeft niet te volgen wiskundige patronen,
maar als het doet het is geweldig om te zien.)
* Opmerkingen over de animatie
Zonnebloempitten groeien vanuit het midden naar buiten, maar bij de animatie vond ik het makkelijker om eerst de jongere zaden te tekenen en dan de oudere toe te voegen.
De animatie zou langer door moeten gaan om hetzelfde te zijn als de zonnebloem – dit zou resulteren in 55 spiralen met de klok mee en 34 spiralen tegen de klok in (opeenvolgende Fibonacci getallen). Ik wilde alleen niet dat het te lang zou duren.
De spiralen zijn er niet in geprogrammeerd – ze ontstaan op natuurlijke wijze als gevolg van het proberen om de zaden zo dicht mogelijk bij elkaar te plaatsen en ze tegelijkertijd op de juiste rotatie te houden.

