
Les plantes peuvent faire pousser de nouvelles cellules en spirale, comme le motif des graines dans ce magnifique tournesol.
La spirale se produit naturellement parce que chaque nouvelle cellule est formée après un tour.
« Nouvelle cellule, puis tour,
puis une autre cellule, puis tour, … »
De combien tourner ?
Donc, si vous étiez une plante, de combien de tour disposeriez-vous entre les nouvelles cellules ?
Si vous ne tournez pas du tout, vous obtenez une ligne droite.
![]()
Mais c’est une très mauvaise conception……. vous voulez quelque chose de rond qui tienne ensemble sans espace.
Pourquoi ne pas essayer de trouver la meilleure valeur pour vous-même ?
Essayez différentes valeurs, comme 0,75, 0,9, 3,1416, 0,62, etc.
Souvenez-vous que vous essayez de faire un motif sans écart du début à la fin :
(Au fait, cela n’a pas d’importance pour la partie entière du nombre, comme 1. ou 5. parce que ce sont des révolutions complètes qui nous ramènent dans la même direction.)
Qu’avez-vous obtenu?
Si vous avez obtenu quelque chose qui se termine par 0,618 (ou 0,382, qui est 1 – 0,618) alors « Félicitations, vous êtes un membre réussi du royaume végétal ! »
 |
C’est parce que le nombre d’or (1.61803…) est la meilleure solution, et le Tournesol l’a découvert à sa manière naturelle. Essayez… ça devrait ressembler à ça. |
Pourquoi ?
Tout nombre qui est une fraction simple (exemple : 0.75 est 3/4, et 0,95 est 19/20, etc) fera, après un certain temps, un modèle de lignes qui s’empilent, ce qui fait des écarts.
Mais le nombre d’or (son symbole est la lettre grecque Phi, montrée à gauche) est un expert pour ne pas être une fraction.
C’est un nombre irrationnel (ce qui signifie qu’on ne peut pas l’écrire comme une simple fraction), mais plus encore… il est aussi loin qu’on puisse l’être d’être proche de toute fraction.
| Il ne suffit pas d’être irrationnel | |
|---|---|
 |
Pi (3,141592654…), qui est également irrationnel. Malheureusement il a une décimale très proche de 1/7 (= 0,142857…), donc il se retrouve avec 7 bras. |
 |
e (2,71828….) également irrationnel, ne fonctionne pas non plus car sa décimale est proche de 5/7 (0,714285…), donc il se retrouve aussi avec 7 bras. |
Alors, comment fonctionne le nombre d’or ?
| L’une des propriétés particulières du nombre d’or est qu’il peut être défini en fonction de lui-même, comme ceci : | |
| (En chiffres : 1,61803… = 1 + 1/1,61803…) | |
| On peut l’étendre en cette fraction qui se prolonge à l’infini (appelée « fraction continue »): | |
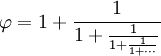 |
|
Elle se glisse donc proprement entre les fractions simples.
Nombres de Fibonacci
Il existe une relation particulière entre le nombre d’or et les nombres de Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21, … etc, chaque nombre est la somme des deux nombres qui le précèdent).
Lorsque nous prenons n’importe quels deux nombres de Fibonacci successifs (l’un après l’autre), leur rapport est très proche du nombre d’or :
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Donc, tout comme nous obtenons naturellement sept bras lorsque nous utilisons 0.142857 (1/7), nous avons tendance à obtenir des nombres de Fibonacci lorsque nous utilisons le nombre d’or.
Essayez de compter les bras de la spirale – les spirales « tournant à gauche », puis les spirales « tournant à droite »… quels nombres avez-vous obtenus ?
Croissance en spirale des feuilles

Ce comportement intéressant ne se trouve pas seulement dans les graines de tournesol.
Les feuilles, les branches et les pétales peuvent aussi pousser en spirale.
Pourquoi ? Pour que les nouvelles feuilles ne bloquent pas le soleil des feuilles plus anciennes, ou pour que le maximum de pluie ou de rosée soit dirigé vers les racines.
En fait, lorsqu’une plante a des spirales, la rotation tend à être une fraction faite avec deux Nombres de Fibonacci successifs (l’un après l’autre), par exemple :
- Une demi-rotation est 1/2 (1 et 2 sont des Nombres de Fibonacci)
- 3/5 est également commun (les deux Nombres de Fibonacci), et
- 5/8 également (vous avez deviné !)
tout cela se rapproche de plus en plus du nombre d’or.
|
Et c’est pourquoi les nombres de Fibonacci sont très courants dans les plantes. Voici une marguerite avec 21 pétales |
 |
Mais nous ne voyons pas cela dans toutes les plantes, car la nature a de nombreuses méthodes différentes de survie.
Angle d’or
Jusqu’ici nous avons parlé de « tours » (rotations complètes).
L’équivalent de 0,61803… rotations est de 222,4922… degrés, soit environ 222,5°.
Dans l’autre sens, il est d’environ 137,5°, appelé « Angle d’or ».
Donc, la prochaine fois que vous vous promenez dans le jardin, cherchez l’Angle d’or,
et comptez les pétales et les feuilles pour trouver les nombres de Fibonacci,
et découvrez à quel point les plantes sont intelligentes… !
Exercice
Pourquoi ne pas aller dans le jardin ou le parc dès maintenant, et commencer à compter les feuilles et les pétales, et mesurer les rotations pour voir ce que vous trouvez.
Vous pouvez écrire vos résultats sur ce formulaire:
| Nom ou description de la plante: | ||
| Les feuilles poussent-elles en spirale ? O / N | ||
| Compter un groupe de feuilles : | ||
| Combien de feuilles (a) ? | ||
| Combien de rotations complètes (b) ? | ||
| Rotation par feuille (b/a) : | ||
| Angle de rotation (360 × b/a) : | ||
| Y a-t-il des fleurs ? O / N | ||
| Combien de pétales sur la fleur 1: | ||
| Fleur 2: | ||
| Fleur 3 : | ||
(Mais rappelez-vous, la nature a ses propres règles, et elle n’a pas à suivre des modèles mathématiques,
mais quand elle le fait, c’est impressionnant à voir.)
* Notes sur l’animation
Les graines de tournesol poussent du centre vers l’extérieur, mais sur l’animation, j’ai trouvé plus facile de dessiner les graines les plus jeunes d’abord et d’ajouter les plus vieilles.
L’animation devrait continuer plus longtemps pour être la même que le tournesol – cela donnerait 55 spirales dans le sens des aiguilles d’une montre et 34 spirales dans le sens inverse (nombres de Fibonacci successifs). Je ne voulais simplement pas que cela prenne trop de temps.
Les spirales n’y sont pas programmées – elles se produisent naturellement en essayant de placer les graines aussi près les unes des autres que possible tout en les gardant à la rotation correcte.
.

