- Modes de chiffrement authentifié avec données supplémentaires (AEAD)Modification
- Compteur de Galois (GCM)Edit
- Compteur avec code d’authentification de message de chaînage de blocs de chiffrement (CCM)Edit
- Vecteur d’initialisation synthétique (SIV)Edit
- AES-GCM-SIVEdit
- Modes de confidentialité uniquementEdit
- Livre de code électronique (ECB)Edit
- Chaînage de blocs de chiffrement (CBC)Edit
- ExempleEdit
- Chaînage par blocs de chiffrement propageant (PCBC)Edit
- Retour de chiffrement (CFB)Edit
- Full-bloc CFBEdit
- CFB-1, CFB-8, CFB-64, CFB-128, etc.Edit
- CFB comparé à d’autres modesEdit
- Rétroaction de sortie (OFB)Edit
- Compteur (CTR)Edit
Modes de chiffrement authentifié avec données supplémentaires (AEAD)Modification
Un certain nombre de modes de fonctionnement ont été conçus pour combiner le secret et l’authentification dans une seule primitive cryptographique. Des exemples de tels modes sont le chaînage par blocs de chiffrement étendu (XCBC), le chaînage par blocs de chiffrement à intégrité reconnue (IACBC), le mode parallélisable à intégrité reconnue (IAPM), OCB, EAX, CWC, CCM et GCM. Les modes de chiffrement authentifié sont classés en modes à passage unique ou à double passage. Certains algorithmes de chiffrement authentifié à passage unique, tels que le mode OCB, sont encombrés de brevets, tandis que d’autres ont été spécifiquement conçus et publiés de manière à éviter un tel encombrement.
En outre, certains modes permettent également l’authentification de données associées non chiffrées, et ceux-ci sont appelés schémas AEAD (chiffrement authentifié avec données associées). Par exemple, le mode EAX est un schéma AEAD à double passage alors que le mode OCB est à passage unique.
Compteur de Galois (GCM)Edit
Compteur de Galois
Oui
.
Oui
Oui
Le mode Galois/compteur (GCM) combine le mode bienconnu du mode compteur de cryptage avec le nouveau mode Galois d’authentification. La principale caractéristique est la facilité de calcul parallèle de la multiplication du champ de Galois utilisée pour l’authentification. Cette caractéristique permet un débit plus élevé que les algorithmes de chiffrement.
Le GMM est défini pour les chiffrements par blocs avec une taille de bloc de 128 bits. Le code d’authentification de message de Galois (GMAC) est une variante d’authentification uniquement du GCM qui peut former un code d’authentification de message incrémental. Le GCM et le GMAC peuvent tous deux accepter des vecteurs d’initialisation de longueur arbitraire. Le GCM peut tirer pleinement parti du traitement parallèle et la mise en œuvre du GCM peut faire un usage efficace d’un pipeline d’instructions ou d’un pipeline matériel. Le mode de fonctionnement CBC subit des décrochages de pipeline qui nuisent à son efficacité et à ses performances.
Comme dans CTR, les blocs sont numérotés séquentiellement, puis ce numéro de bloc est combiné avec un IV et crypté avec un chiffrement par blocs E, généralement AES. Le résultat de ce chiffrement est ensuite soumis à un XOR avec le texte en clair pour produire le texte chiffré. Comme tous les modes de comptage, il s’agit essentiellement d’un chiffrement par flux, et il est donc essentiel qu’un IV différent soit utilisé pour chaque flux qui est chiffré.

Les blocs de texte chiffré sont considérés comme des coefficients d’un polynôme qui est ensuite évalué à un point H dépendant de la clé, en utilisant l’arithmétique des champs finis. Le résultat est ensuite chiffré, produisant une étiquette d’authentification qui peut être utilisée pour vérifier l’intégrité des données. Le texte chiffré contient alors le IV, le texte chiffré et l’étiquette d’authentification.
Compteur avec code d’authentification de message de chaînage de blocs de chiffrement (CCM)Edit
Compteur avec code d’authentification de message de chaînage de blocs de chiffrement (compteur avec CBC-MAC ; CCM) est un algorithme de chiffrement authentifié conçu pour fournir à la fois l’authentification et la confidentialité. Le mode CCM est uniquement défini pour les chiffrements par blocs avec une longueur de bloc de 128 bits.
Vecteur d’initialisation synthétique (SIV)Edit
Le vecteur d’initialisation synthétique (SIV) est un mode de chiffrement par blocs résistant aux nonce-misuse.
SIV synthétise un IV interne en utilisant la une fonction pseudo-aléatoire S2V. S2V est un hachage à clé est basé sur CMAC, et l’entrée de la fonction est:
- Données authentifiées supplémentaires (zéro, un ou plusieurs champs AAD sont supportés)
- Plaintexte
- Clé d’authentification (K1).
SIV chiffre la sortie S2V et le texte en clair en utilisant AES-CTR, avec la clé de chiffrement (K2).
SIV peut supporter un chiffrement authentifié externe basé sur un nonce, auquel cas l’un des champs de données authentifiées est utilisé à cette fin. La RFC5297 précise qu’à des fins d’interopérabilité, le dernier champ de données authentifiées doit être utilisé nonce externe.
En raison de l’utilisation de deux clés, la clé d’authentification K1 et la clé de chiffrement K2, les schémas de dénomination des variantes SIV AEAD peuvent entraîner une certaine confusion ; par exemple AEAD_AES_SIV_CMAC_256 fait référence à AES-SIV avec deux clés AES-128 et non AES-256.
AES-GCM-SIVEdit
AES-GCM-SIV est un mode de fonctionnement pour l’Advanced Encryption Standard qui fournit des performances similaires au mode Galois/compteur ainsi qu’une résistance aux abus en cas de réutilisation d’un nonce cryptographique. La construction est définie dans le RFC 8452.
AES-GCM-SIV synthétise l’IV interne. Il dérive un hachage des données authentifiées supplémentaires et du texte en clair en utilisant la fonction de hachage de Galois POLYVAL. Le hachage est ensuite crypté une clé AES, et utilisé comme balise d’authentification et vecteur d’initialisation AES-CTR.
AES-GCM-SIV est une amélioration de l’algorithme GCM-SIV au nom très similaire, avec quelques très petits changements (par ex. comment AES-CTR est initialisé), mais qui apporte des avantages pratiques à sa sécurité « Cet ajout permet de chiffrer jusqu’à 250 messages avec la même clé, par rapport à la limitation importante de seulement 232 messages qui étaient autorisés avec GCM-SIV. »
Modes de confidentialité uniquementEdit
De nombreux modes de fonctionnement ont été définis. Certains d’entre eux sont décrits ci-dessous. Le but des modes de chiffrement est de masquer les motifs qui existent dans les données chiffrées, comme illustré dans la description de la faiblesse de l’ECB.
Les différents modes de chiffrement masquent les motifs en cascadant les sorties du bloc de chiffrement ou d’autres variables globalement déterministes dans le bloc de chiffrement suivant. Les entrées des modes énumérés sont résumées dans le tableau suivant :
| Mode | Formules | Ciphertext | |
|---|---|---|---|
| Livre de code électronique | (ECB) | Yi = F(PlainTexti, Key) | Yi |
| Cipher block chaining | (CBC) | Yi = PlainTexti XOR Ciphertexti-1 | F(Y, Key) ; Ciphertext0 = IV |
| Propagation CBC | (PCBC) | Yi = PlainTexti XOR (Ciphertexti-1 XOR PlainTexti-1) | F(Y, Clé) ; Ciphertext0 = IV |
| Cipher feedback | (CFB) | Yi = Ciphertexti-1 | Plaintext XOR F(Y, Key) ; Ciphertext0 = IV |
| Rétroaction de sortie | (OFB) | Yi = F(Yi-1, Clé) ; Y0 = F(IV, Clé) | Plaintexte XOR Yi |
| Compteur | (CTR) | Yi = F(IV + g(i), Clé) ; IV = token() | Plaintexte XOR Yi |
Note : g(i) est une fonction déterministe quelconque, souvent la fonction identité.
Livre de code électronique (ECB)Edit
Livre de code électronique
Oui
.
Oui
Oui
Le plus simple des modes de chiffrement est le mode livre de code électronique (ECB) (nommé d’après les livres de code physiques conventionnels). Le message est divisé en blocs, et chaque bloc est chiffré séparément.
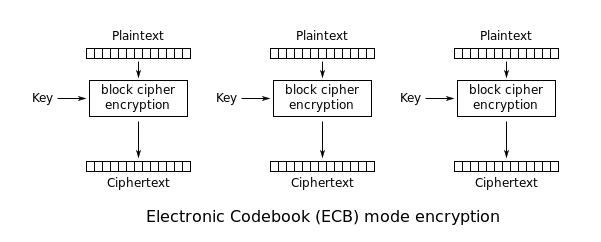

L’inconvénient de cette méthode est un manque de diffusion. Comme l’ECB chiffre des blocs de texte en clair identiques dans des blocs de texte chiffré identiques, il ne cache pas bien les motifs de données.L’ECB n’est pas recommandé pour une utilisation dans les protocoles cryptographiques.
Un exemple frappant du degré auquel l’ECB peut laisser des motifs de données en clair dans le texte chiffré peut être vu lorsque le mode ECB est utilisé pour chiffrer une image bitmap qui utilise de grandes zones de couleur uniforme. Bien que la couleur de chaque pixel individuel soit chiffrée, l’image globale peut encore être discernée, car le motif des pixels de couleur identique dans l’original reste dans la version chiffrée.
Le mode ECB peut également rendre les protocoles sans protection d’intégrité encore plus sensibles aux attaques par rejeu, puisque chaque bloc est décrypté exactement de la même manière.
Chaînage de blocs de chiffrement (CBC)Edit
Chaînage de blocs de chiffrement
.
Non
Oui
Oui
Ehrsam, Meyer, Smith et Tuchman ont inventé le mode de fonctionnement par enchaînement de blocs de chiffrement (CBC) en 1976. En mode CBC, chaque bloc de texte en clair est soumis à un XOR avec le bloc de texte chiffré précédent avant d’être chiffré. De cette façon, chaque bloc de texte chiffré dépend de tous les blocs de texte en clair traités jusqu’à ce point. Pour que chaque message soit unique, un vecteur d’initialisation doit être utilisé dans le premier bloc.
Si le premier bloc a l’indice 1, la formule mathématique du chiffrement CBC est
C i = E K ( P i ⊕ C i – 1 ) , {\displaystyle C_{i}=E_{K}(P_{i}\oplus C_{i-1}),}

C 0 = I V , {\displaystyle C_{0}=IV,}

alors que la formule mathématique du décryptage CBC est
P i = D K ( C i ) ⊕ C i – 1 , {\displaystyle P_{i}=D_{K}(C_{i})\oplus C_{i-1},}

C 0 = I V . {\displaystyle C_{0}=IV.}

ExempleEdit
CBC a été le mode de fonctionnement le plus utilisé. Ses principaux inconvénients sont que le chiffrement est séquentiel (c’est-à-dire qu’il ne peut pas être parallélisé), et que le message doit être paddé à un multiple de la taille du bloc de chiffrement. L’un des moyens de résoudre ce dernier problème consiste à utiliser la méthode connue sous le nom de vol de texte chiffré. Notez qu’un changement d’un bit dans un texte en clair ou un vecteur d’initialisation (IV) affecte tous les blocs de texte chiffré suivants.
Le déchiffrement avec l’IV incorrect entraîne la corruption du premier bloc de texte en clair, mais les blocs de texte en clair suivants seront corrects. Cela est dû au fait que chaque bloc est soumis à un XOR avec le texte chiffré du bloc précédent, et non le texte en clair, de sorte que l’on n’a pas besoin de déchiffrer le bloc précédent avant de l’utiliser comme IV pour le déchiffrement du bloc actuel. Cela signifie qu’un bloc de texte en clair peut être récupéré à partir de deux blocs adjacents de texte chiffré. Par conséquent, le décryptage peut être parallélisé. Notez qu’une modification d’un bit du texte chiffré entraîne la corruption complète du bloc de texte en clair correspondant, et inverse le bit correspondant dans le bloc de texte en clair suivant, mais le reste des blocs reste intact. Cette particularité est exploitée dans différentes attaques par oracle de remplissage, comme POODLE.
Les vecteurs d’initialisation explicites tirent parti de cette propriété en faisant précéder le texte en clair d’un seul bloc aléatoire. Le chiffrement se fait normalement, sauf que l’IV n’a pas besoin d’être communiqué à la routine de déchiffrement. Quel que soit le IV utilisé par le décryptage, seul le bloc aléatoire est « corrompu ». Il peut être jeté en toute sécurité et le reste du décryptage est le texte en clair original.
Chaînage par blocs de chiffrement propageant (PCBC)Edit
Chaînage par blocs de chiffrement propageant
.
Non
Non
Non
Le mode de chaînage de blocs de chiffrement à propagation ou de chiffrement en texte clair-Le mode de chaînage de blocs a été conçu pour que de petites modifications du texte chiffré se propagent indéfiniment lors du déchiffrement, ainsi que lors du cryptage. En mode PCBC, chaque bloc de texte en clair est soumis à une opération XOR avec le bloc de texte en clair précédent et le bloc de texte chiffré précédent avant d’être chiffré. Comme pour le mode CBC, un vecteur d’initialisation est utilisé dans le premier bloc.
Les algorithmes de chiffrement et de déchiffrement sont les suivants :
C i = E K ( P i ⊕ P i – 1 ⊕ C i – 1 ) , P 0 ⊕ C 0 = I V , {\displaystyle C_{i}=E_{K}(P_{i}\oplus P_{i-1}\oplus C_{i-1}),P_{0}\oplus C_{0}=IV,}

P i = D K ( C i ) ⊕ P i – 1 ⊕ C i – 1 , P 0 ⊕ C 0 = I V . {\displaystyle P_{i}=D_{K}(C_{i})}\oplus P_{i-1}\oplus C_{i-1},P_{0}\oplus C_{0}=IV.}

PCBC est utilisé dans Kerberos v4 et WASTE, notamment, mais n’est pas courant autrement. Sur un message chiffré en mode PCBC, si deux blocs de texte chiffré adjacents sont échangés, cela n’affecte pas le déchiffrement des blocs suivants. Pour cette raison, le mode PCBC n’est pas utilisé dans Kerberos v5.
Retour de chiffrement (CFB)Edit
Full-bloc CFBEdit
Cipher feedback
Non
.
Oui
Oui
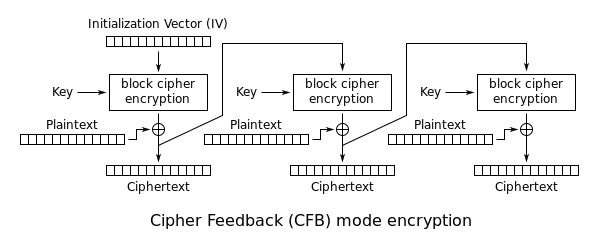
Le mode rétroaction de chiffrement (CFB), dans sa forme la plus simple, consiste à utiliser la totalité de la sortie du chiffrement par blocs. Dans cette variation, il est très similaire au CBC, fait d’un chiffrement par blocs un chiffrement par flux auto-synchronisant. Le décryptage CFB dans cette variation est presque identique au cryptage CBC effectué en sens inverse :
C i = {IV , i = 0 E K ( C i – 1 ) ⊕ P i , sinon P i = E K ( C i – 1 ) ⊕ C i , {\displaystyle {\begin{aligned}C_{i}&={\begin{cases}{\text{IV}},&i=0\\E_{K}(C_{i-1})\oplus P_{i},&{\text{otherwise}}\end{cases}}\\P_{i}&=E_{K}(C_{i-1})\oplus C_{i},\end{aligned}}}


CFB-1, CFB-8, CFB-64, CFB-128, etc.Edit
NIST SP800-38A définit CFB avec une largeur de bit. Le mode CFB requiert également un paramètre entier, noté s, tel que 1 ≤ s ≤ b. Dans la spécification du mode CFB ci-dessous, chaque segment de texte en clair (Pj) et chaque segment de texte chiffré (Cj) est constitué de s bits. La valeur de s est parfois incorporée dans le nom du mode, par exemple, le mode CFB 1 bit, le mode CFB 8 bits, le mode CFB 64 bits ou le mode CFB 128 bits.
Ces modes tronqueront la sortie du chiffrement par blocs sous-jacent.
I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}

I i = ( ( I i – 1 ≪ s ) + C i ) mod 2 b , {\displaystyle I_{i}={\big (}(I_{i-1}\ll s)+C_{i}{\big )}{\bmod {2}^{b},}

C i = MSB s ( E K ( I – 1 ) ) ) ⊕ P i , {\displaystyle C_{i}=\operatorname {MSB} _{s}{\big (}E_{K}(I_{i-1}){\big )}\oplus P_{i},}

P i = MSB s ( E K ( I i – 1 ) ) ⊕ C i , {\displaystyle P_{i}=\operatorname {MSB} _{s}{\big (}E_{K}(I_{i-1}){\big )}\oplus C_{i},}

CFB-1 est considéré comme auto-synchronisant et résilient à la perte de texte chiffré ; « Lorsque le mode CFB 1 bit est utilisé, alors la synchronisation est automatiquement restaurée b+1 positions après le bit inséré ou supprimé. Pour d’autres valeurs de s dans le mode CFB, et pour les autres modes de confidentialité de cette recommandation, la synchronisation doit être restaurée de manière externe. » (NIST SP800-38A). C’est-à-dire que la perte d’un bit dans un chiffrement par blocs de 128 bits de largeur comme AES rendra 129 bits invalides avant d’émettre des bits valides.
CFB peut également s’auto-synchroniser dans certains cas particuliers autres que ceux spécifiés. Par exemple, un changement d’un bit dans CFB-128 avec un chiffrement par bloc sous-jacent de 128 bits, se resynchronisera après deux blocs. (Cependant, CFB-128 etc ne gérera pas la perte de bits de manière gracieuse ; une perte d’un bit fera perdre au déchiffreur son alignement avec le chiffreur)
CFB comparé à d’autres modesEdit
Comme le mode CBC, les changements dans le texte en clair se propagent à jamais dans le texte chiffré, et le chiffrement ne peut pas être parallélisé. Toujours comme le mode CBC, le déchiffrement peut être parallélisé.
CFB, OFB et CTR partagent deux avantages par rapport au mode CBC : le chiffrement par blocs n’est jamais utilisé que dans le sens du chiffrement, et le message n’a pas besoin d’être capitonné à un multiple de la taille du bloc de chiffrement (bien que le vol de texte chiffré puisse également être utilisé pour le mode CBC afin de rendre le capitonnage inutile).
Rétroaction de sortie (OFB)Edit
Rétroaction de sortie
Non
Non
Non
Le mode de rétroaction de sortie (OFB) transforme un chiffrement par blocs en un chiffrement par flux synchrone. Il génère des blocs de flux de clés, qui sont ensuite soumis à un XOR avec les blocs de texte en clair pour obtenir le texte chiffré. Tout comme avec les autres chiffrages par flux, le fait de retourner un bit dans le texte chiffré produit un bit retourné dans le texte en clair au même endroit. Cette propriété permet à de nombreux codes correcteurs d’erreurs de fonctionner normalement même lorsqu’ils sont appliqués avant le chiffrement.
En raison de la symétrie de l’opération XOR, le chiffrement et le déchiffrement sont exactement les mêmes :
C j = P j ⊕ O j , {\displaystyle C_{j}=P_{j}\oplus O_{j},}

P j = C j ⊕ O j , {\displaystyle P_{j}=C_{j}\oplus O_{j},}

O j = E K ( I j ) , {\displaystyle O_{j}=E_{K}(I_{j}),}

I j = O j – 1 , {\displaystyle I_{j}=O_{j-1},}

I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}


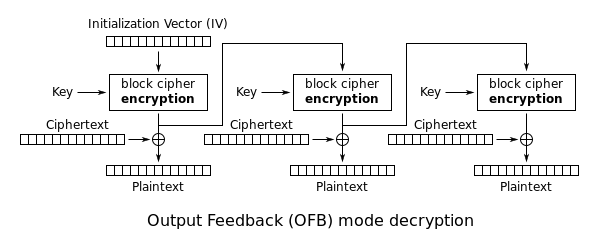
Chaque opération de chiffrement par blocs avec rétroaction en sortie dépend de toutes les précédentes, et ne peut donc pas être effectuée en parallèle. Cependant, comme le texte en clair ou le texte chiffré n’est utilisé que pour le XOR final, les opérations de chiffrement par blocs peuvent être effectuées à l’avance, ce qui permet d’effectuer l’étape finale en parallèle une fois que le texte en clair ou le texte chiffré est disponible.
Il est possible d’obtenir un flux de clés en mode OFB en utilisant le mode CBC avec une chaîne constante de zéros en entrée. Cela peut être utile, car cela permet d’utiliser des implémentations matérielles rapides du mode CBC pour le cryptage en mode OFB.
L’utilisation du mode OFB avec un bloc partiel comme rétroaction comme le mode CFB réduit la longueur moyenne du cycle par un facteur de 232 ou plus. Un modèle mathématique proposé par Davies et Parkin et corroboré par des résultats expérimentaux a montré que ce n’est qu’avec une rétroaction complète qu’il est possible d’obtenir une longueur moyenne de cycle proche du maximum pouvant être obtenu. Pour cette raison, le support de la rétroaction tronquée a été supprimé de la spécification de l’OFB.
Compteur (CTR)Edit
Compteur
.
Oui
Oui
Oui
Note : Le mode CTR (CM) est également connu sous le nom de mode compteur d’entiers (ICM) et de mode compteur d’entiers segmenté (SIC).
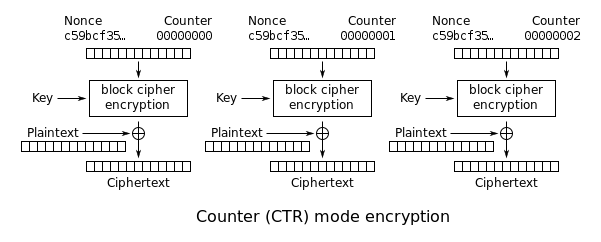
Comme OFB, le mode compteur transforme un chiffrement par bloc en un chiffrement par flux. Il génère le bloc de flux de clés suivant en chiffrant les valeurs successives d’un « compteur ». Le compteur peut être n’importe quelle fonction qui produit une séquence qui est garantie de ne pas se répéter pendant une longue période, bien qu’un compteur réel d’incrémentation par un soit le plus simple et le plus populaire. L’utilisation d’une simple fonction d’entrée déterministe était autrefois controversée ; les critiques soutenaient que « l’exposition délibérée d’un cryptosystème à une entrée systématique connue représente un risque inutile ». Cependant, aujourd’hui, le mode CTR est largement accepté et tout problème est considéré comme une faiblesse du chiffrement par blocs sous-jacent, qui est censé être sûr indépendamment du biais systémique de son entrée. Avec le CBC, le mode CTR est l’un des deux modes de chiffrement par blocs recommandés par Niels Ferguson et Bruce Schneier.
Le mode CTR a été introduit par Whitfield Diffie et Martin Hellman en 1979.
Le mode CTR a des caractéristiques similaires à l’OFB, mais permet également une propriété d’accès aléatoire pendant le déchiffrement. Le mode CTR est bien adapté pour fonctionner sur une machine multiprocesseur où les blocs peuvent être chiffrés en parallèle. De plus, il ne souffre pas du problème de cycle court qui peut affecter l’OFB.
Si l’IV/nonce est aléatoire, alors ils peuvent être combinés avec le compteur en utilisant n’importe quelle opération inversible (concaténation, addition, ou XOR) pour produire le bloc de compteur unique réel pour le cryptage. Dans le cas d’un nonce non aléatoire (comme un compteur de paquets), le nonce et le compteur doivent être concaténés (par exemple, en stockant le nonce dans les 64 bits supérieurs et le compteur dans les 64 bits inférieurs d’un bloc de compteur de 128 bits). Le simple fait d’ajouter ou de soumettre à un test XOR le nonce et le compteur en une seule valeur compromettrait la sécurité dans le cas d’une attaque par texte choisi dans de nombreux cas, car l’attaquant pourrait être en mesure de manipuler l’ensemble de la paire IV-compteur pour provoquer une collision. Une fois qu’un attaquant contrôle la paire IV-compteur et le texte en clair, le XOR du texte chiffré avec le texte en clair connu donnerait une valeur qui, lorsqu’elle est XORée avec le texte chiffré de l’autre bloc partageant la même paire IV-compteur, décrypterait ce bloc.
Notez que le nonce dans ce diagramme est équivalent au vecteur d’initialisation (IV) dans les autres diagrammes. Cependant, si les informations de décalage/localisation sont corrompues, il sera impossible de récupérer partiellement ces données en raison de la dépendance au décalage d’octet.
.