Biographie
On se souvient surtout de Johannes Kepler pour avoir découvert les trois lois du mouvement planétaire qui portent son nom publiées en 1609 et 1619). Il a également réalisé d’importants travaux en optique (1604, 1611), découvert deux nouveaux polyèdres réguliers (1619), donné le premier traitement mathématique de l’emballage serré de sphères égales (conduisant à une explication de la forme des cellules d’un nid d’abeille, 1611), donné la première preuve du fonctionnement des logarithmes (1624), et conçu une méthode pour trouver les volumes des solides de révolution qui (avec le recul !) peut être considérée comme contribuant au développement du calcul (1615, 1616). En outre, il a calculé les tables astronomiques les plus exactes connues jusqu’alors, dont l’exactitude continue a beaucoup contribué à établir la vérité de l’astronomie héliocentrique (Tables Rudolphes, Ulm, 1627).
Une grande quantité de la correspondance de Kepler subsiste. Beaucoup de ses lettres sont presque l’équivalent d’un article scientifique (il n’y avait pas encore de journaux scientifiques), et les correspondants semblent les avoir conservées parce qu’elles étaient intéressantes. En conséquence, nous en savons beaucoup sur la vie de Kepler, et même sur son caractère. C’est en partie à cause de cela que Kepler a eu une sorte de carrière de personnage plus ou moins fictif (voir la note historiographique ci-dessous).
Enfance
Kepler est né dans la petite ville de Weil der Stadt en Souabe et s’installe avec ses parents dans la ville voisine de Leonberg en 1576. Son père est un soldat mercenaire et sa mère est la fille d’un aubergiste. Johannes est leur premier enfant. Son père quitte la maison pour la dernière fois lorsque Johannes a cinq ans, et on pense qu’il est mort pendant la guerre aux Pays-Bas. Enfant, Kepler vit avec sa mère dans l’auberge de son grand-père. Il nous raconte qu’il avait l’habitude d’aider en servant dans l’auberge. On imagine que les clients étaient parfois déconcertés par les compétences inhabituelles de l’enfant en arithmétique.
Les premières études de Kepler se déroulent dans une école locale, puis dans un séminaire voisin, d’où il sort, dans l’intention d’être ordonné, pour s’inscrire à l’université de Tübingen, alors (comme aujourd’hui) un bastion de l’orthodoxie luthérienne.
Les opinions de Kepler
Toute sa vie, Kepler est un homme profondément religieux. Tous ses écrits contiennent de nombreuses références à Dieu, et il considérait son travail comme l’accomplissement de son devoir chrétien de comprendre les œuvres de Dieu. L’homme étant, selon Kepler, créé à l’image de Dieu, il est clairement capable de comprendre l’Univers qu’Il a créé. De plus, Kepler est convaincu que Dieu a créé l’Univers selon un plan mathématique (une croyance que l’on retrouve dans les œuvres de Platon et associée à Pythagore). Comme il était généralement admis à l’époque que les mathématiques fournissaient une méthode sûre pour parvenir à des vérités sur le monde (les notions et postulats communs d’Euclide étant considérés comme réellement vrais), nous avons ici une stratégie pour comprendre l’Univers. Comme certains auteurs ont taxé Kepler d’irrationalité, il convient de noter que cette épistémologie plutôt optimiste est en effet très éloignée de la conviction du mystique selon laquelle les choses ne peuvent être comprises que de manière imprécise, en s’appuyant sur des intuitions non soumises à la raison. Kepler remercie en effet à plusieurs reprises Dieu de lui avoir accordé des intuitions, mais celles-ci sont présentées comme rationnelles.
L’enseignement universitaire
À cette époque, il était habituel pour tous les étudiants d’une université de suivre des cours de « mathématiques ». En principe, cela comprenait les quatre sciences mathématiques : arithmétique, géométrie, astronomie et musique. Il semble toutefois que l’enseignement dispensé dépende de l’université concernée. À Tübingen, Kepler reçoit des cours d’astronomie dispensés par l’un des principaux astronomes de l’époque, Michael Mästlin (1550 – 1631). L’astronomie du programme d’études était, bien entendu, l’astronomie géocentrique, c’est-à-dire la version actuelle du système ptolémaïque, dans lequel les sept planètes – Lune, Mercure, Vénus, Soleil, Mars, Jupiter et Saturne – se déplacent autour de la Terre, leurs positions par rapport aux étoiles fixes étant calculées en combinant les mouvements circulaires. Ce système était plus ou moins en accord avec les notions courantes (aristotéliciennes) de la physique, bien qu’il y ait certaines difficultés, comme celle de savoir si l’on pouvait considérer comme « uniforme » (et donc acceptable comme manifestement éternel) un mouvement circulaire qui n’était pas uniforme autour de son propre centre mais autour d’un autre point (appelé « équant »). Cependant, il semble que, dans l’ensemble, les astronomes (qui se considéraient comme des « mathématiciens ») se contentaient de calculer la position des planètes et laissaient aux philosophes naturels le soin de se demander si les modèles mathématiques correspondaient aux mécanismes physiques. Kepler n’a pas adopté cette attitude. Son premier ouvrage publié (1596) propose de considérer les trajectoires réelles des planètes, et non les cercles utilisés pour les construire.
A Tübingen, Kepler étudie non seulement les mathématiques mais aussi le grec et l’hébreu (tous deux nécessaires pour lire les écritures dans leur langue d’origine). L’enseignement se faisait en latin. À la fin de sa première année, Kepler obtient des « A » pour tout, sauf les mathématiques. Mästlin essaie probablement de lui dire qu’il peut faire mieux, car Kepler est en fait l’un des élèves sélectionnés à qui il choisit d’enseigner l’astronomie plus avancée en leur présentant le nouveau système cosmologique héliocentrique de Copernic. C’est par Mästlin que Kepler a appris que la préface de Sur les révolutions, expliquant qu’il ne s’agissait que de « mathématiques », n’était pas de Copernic. Kepler semble avoir accepté presque instantanément que le système copernicien était physiquement vrai ; les raisons pour lesquelles il l’a accepté seront discutées en relation avec son premier modèle cosmologique (voir ci-dessous).
Il semble que même à l’époque où Kepler était étudiant, il y avait des indications que ses croyances religieuses n’étaient pas entièrement en accord avec le luthéranisme orthodoxe courant à Tübingen et formulé dans la Confessio Augustana Ⓣ. Les problèmes de Kepler avec cette orthodoxie protestante concernent la relation supposée entre la matière et l' »esprit » (une entité non matérielle) dans la doctrine de l’Eucharistie. Ceci est lié à l’astronomie de Kepler dans la mesure où il a apparemment rencontré des difficultés intellectuelles similaires pour expliquer comment la « force » du Soleil pouvait affecter les planètes. Dans ses écrits, Kepler a l’habitude d’exposer ses opinions, ce qui est très pratique pour les historiens. Dans la vie réelle, il est probable qu’une tendance similaire à la franchise ait conduit les autorités de Tübingen à entretenir des doutes fondés sur son orthodoxie religieuse. Cela pourrait expliquer pourquoi Mästlin a persuadé Kepler d’abandonner ses projets d’ordination et d’accepter un poste d’enseignant de mathématiques à Graz. L’intolérance religieuse s’accentue au cours des années suivantes. Kepler est excommunié en 1612. Cela lui cause beaucoup de peine, mais malgré son statut social (à l’époque) relativement élevé, en tant que mathématicien impérial, il ne réussit jamais à faire lever l’interdiction.
Le premier modèle cosmologique de Kepler (1596)
Au lieu des sept planètes de l’astronomie géocentrique standard, le système copernicien n’en comptait que six, la Lune étant devenue un corps d’un genre jusqu’alors inconnu de l’astronomie, que Kepler appellera plus tard un « satellite » (un nom qu’il a inventé en 1610 pour décrire les lunes que Galilée avait découvertes en orbite autour de Jupiter, signifiant littéralement « accompagnateur »). Pourquoi six planètes ?
De plus, dans l’astronomie géocentrique, il n’y avait aucun moyen d’utiliser des observations pour trouver les tailles relatives des orbes planétaires ; on supposait simplement qu’ils étaient en contact. Cela ne semblait pas nécessiter d’explication, car cela correspondait parfaitement à la croyance des philosophes naturels selon laquelle l’ensemble du système tournait à partir du mouvement de la sphère la plus extérieure, une (ou peut-être deux) au-delà de la sphère des étoiles « fixes » (celles dont le dessin forme les constellations), au-delà de la sphère de Saturne. Dans le système copernicien, le fait que la composante annuelle de chaque mouvement planétaire soit le reflet du mouvement annuel de la Terre permettait d’utiliser les observations pour calculer la taille de la trajectoire de chaque planète, et il s’est avéré qu’il y avait des espaces énormes entre les planètes. Pourquoi ces espaces particuliers ?
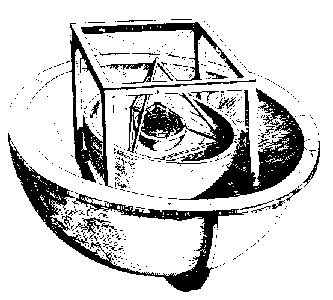
La réponse de Kepler à ces questions, décrite dans son Mysterium cosmographicum Ⓣ, Tübingen, 1596, paraît bizarre aux lecteurs du XXe siècle (voir la figure de droite). Il a suggéré que si une sphère était dessinée pour toucher l’intérieur de la trajectoire de Saturne, et qu’un cube était inscrit dans la sphère, alors la sphère inscrite dans ce cube serait la sphère circonscrivant la trajectoire de Jupiter. Ensuite, si un tétraèdre régulier était dessiné dans la sphère inscrivant le chemin de Jupiter, l’intérieur du tétraèdre serait la sphère circonscrivant le chemin de Mars, et ainsi de suite vers l’intérieur, mettant le dodécaèdre régulier entre Mars et la Terre, l’icosaèdre régulier entre la Terre et Vénus, et l’octaèdre régulier entre Vénus et Mercure. Cela explique parfaitement le nombre de planètes : il n’existe que cinq solides réguliers convexes (comme le prouvent les Éléments d’Euclide, livre 13). Il donne également une correspondance convaincante avec les tailles des trajectoires déduites par Copernic, l’erreur la plus importante étant inférieure à 10% (ce qui est spectaculairement bon pour un modèle cosmologique, même aujourd’hui). Kepler ne s’est pas exprimé en termes de pourcentage d’erreurs, et le sien est en fait le premier modèle cosmologique mathématique, mais il est facile de voir pourquoi il pensait que les preuves observationnelles soutenaient sa théorie.
Kepler considérait que sa théorie cosmologique fournissait des preuves pour la théorie copernicienne. Avant de présenter sa propre théorie, il a donné des arguments pour établir la plausibilité de la théorie copernicienne elle-même. Kepler affirme que ses avantages par rapport à la théorie géocentrique résident dans son plus grand pouvoir explicatif. Par exemple, la théorie copernicienne peut expliquer pourquoi Vénus et Mercure ne sont jamais vues très loin du Soleil (elles se trouvent entre la Terre et le Soleil) alors que dans la théorie géocentrique, il n’y a aucune explication de ce fait. Kepler énumère neuf questions de ce type dans le premier chapitre du Mysterium cosmographicum Ⓣ.
Kepler a réalisé ce travail alors qu’il enseignait à Graz, mais le livre a été vu par la presse à Tübingen par Mästlin. L’accord avec les valeurs déduites de l’observation n’était pas exact, et Kepler espérait que de meilleures observations amélioreraient l’accord, il a donc envoyé une copie du Mysterium cosmographicum à l’un des principaux astronomes observateurs de l’époque, Tycho Brahe (1546 – 1601). Tycho, qui travaillait alors à Prague (à l’époque la capitale du Saint-Empire romain germanique), avait en fait déjà écrit à Mästlin pour lui demander un assistant mathématique. Kepler obtint le poste.
La « guerre avec Mars »
Comme il fallait s’y attendre, les priorités de Tycho n’étaient pas les mêmes que celles de Kepler, et ce dernier se retrouva rapidement à travailler sur le problème insoluble de l’orbite de Mars . Il continue à travailler sur ce problème après la mort de Tycho (en 1601) et Kepler lui succède comme mathématicien impérial. Par convention, les orbites étaient composées de cercles, et assez peu de valeurs d’observation étaient nécessaires pour fixer les rayons et les positions relatives des cercles. Tycho avait fait un nombre considérable d’observations et Kepler était déterminé à en faire le meilleur usage possible. En fait, il disposait d’un tel nombre d’observations qu’une fois qu’il avait construit une orbite possible, il pouvait la vérifier en la comparant à d’autres observations jusqu’à ce qu’un accord satisfaisant soit atteint. Kepler a conclu que l’orbite de Mars était une ellipse avec le Soleil dans l’un de ses foyers (un résultat qui, une fois étendu à toutes les planètes, est maintenant appelé « première loi de Kepler »), et qu’une ligne reliant la planète au Soleil balayait des surfaces égales en des temps égaux pendant que la planète décrivait son orbite (« deuxième loi de Kepler »), c’est-à-dire que la surface est utilisée comme mesure du temps. Après la publication de ce travail dans Astronomia nova, …. Ⓣ, Heidelberg, 1609, Kepler a trouvé des orbites pour les autres planètes, établissant ainsi que les deux lois s’appliquaient également à elles. Les deux lois relient le mouvement de la planète au Soleil ; le copernicanisme de Kepler était crucial pour son raisonnement et ses déductions.
Le processus réel de calcul pour Mars était immensément laborieux – il existe près d’un millier de feuilles folio d’arithmétique qui ont survécu – et Kepler lui-même fait référence à ce travail comme étant » ma guerre avec Mars « , mais le résultat était une orbite qui concorde avec les résultats modernes si exactement que la comparaison doit tenir compte des changements séculaires de l’orbite depuis l’époque de Kepler.
Erreur d’observation
Il était crucial pour la méthode de Kepler de vérifier les orbites possibles par rapport aux observations qu’il ait une idée de ce qui devrait être accepté comme un accord adéquat. De là découle la première utilisation explicite du concept d’erreur d’observation. Kepler peut avoir dû cette notion, au moins en partie, à Tycho, qui procédait à des vérifications détaillées des performances de ses instruments (voir la biographie de Brahe).
Optique, et la nouvelle étoile de 1604
Le travail sur Mars est essentiellement terminé en 1605, mais il y a des retards dans la publication du livre. Pendant ce temps, en réponse aux préoccupations concernant la différence de diamètre apparent de la Lune lorsqu’elle est observée directement et lorsqu’elle est observée à l’aide d’une chambre obscure, Kepler fait quelques travaux sur l’optique, et propose la première théorie mathématique correcte de la chambre obscure et la première explication correcte du fonctionnement de l’œil humain, avec une image à l’envers formée sur la rétine. Ces résultats ont été publiés dans Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Francfort, 1604. Il a également écrit sur la Nouvelle étoile de 1604, maintenant généralement appelée » supernova de Kepler « , rejetant de nombreuses explications, et remarquant à un moment donné que, bien sûr, cette étoile pourrait juste être une création spéciale » mais avant d’en venir à je pense que nous devrions essayer tout le reste » De stella nova Ⓣ, Prague, 1606, chapitre 22, KGW 1, p. 257, ligne 23.
A la suite de l’utilisation du télescope par Galilée pour découvrir les lunes de Jupiter, publiée dans son Messager sidéral (Venise, 1610), à laquelle Kepler avait écrit une réponse enthousiaste (1610), Kepler rédige une étude des propriétés des lentilles (le premier travail de ce type sur l’optique) dans laquelle il présente une nouvelle conception de télescope, utilisant deux lentilles convexes (Dioptrice, Prague, 1611). Ce modèle, dans lequel l’image finale est inversée, a connu un tel succès qu’il est aujourd’hui généralement connu non pas sous le nom de télescope képlérien, mais simplement sous celui de télescope astronomique.
Quitter Prague pour Linz
Les années de Kepler à Prague ont été relativement paisibles, et scientifiquement extrêmement productives. En fait, même lorsque les choses vont mal, il semble n’avoir jamais laissé les circonstances extérieures l’empêcher de poursuivre son travail. Les choses commencent à aller très mal à la fin de 1611. Tout d’abord, son fils de sept ans meurt. Kepler écrit à un ami que cette mort est particulièrement difficile à supporter car l’enfant lui rappelle beaucoup lui-même à cet âge. Puis la femme de Kepler meurt. Puis l’empereur Rodolphe, dont la santé est défaillante, est contraint d’abdiquer en faveur de son frère Matthias, qui, comme Rodolphe, est catholique mais (contrairement à Rodolphe) ne croit pas à la tolérance envers les protestants. Kepler doit quitter Prague. Avant de partir, il fait déplacer le corps de sa femme dans la tombe de son fils et leur écrit une épitaphe en latin. Lui et ses autres enfants s’installent à Linz (aujourd’hui en Autriche).
Mariage et tonneaux de vin
Kepler semble avoir épousé sa première femme, Barbara, par amour (bien que le mariage ait été arrangé par un courtier). Le second mariage, en 1613, était une question de nécessité pratique ; il avait besoin de quelqu’un pour s’occuper des enfants. La nouvelle épouse de Kepler, Susanna, reçoit un cours accéléré sur le caractère de Kepler : la lettre dédicatoire du livre qui en résulte explique que, lors des célébrations du mariage, il a remarqué que les volumes des tonneaux de vin étaient estimés au moyen d’une tige glissée en diagonale à travers le trou de bonde, et il a commencé à se demander comment cela pouvait fonctionner. Il en résulte une étude des volumes des solides de révolution Nova stereometria doliorum … Ⓣ, Linz, 1615, dans laquelle Kepler, se basant sur les travaux d’Archimède, utilise une résolution en « indivisibles ». Cette méthode a été développée plus tard par Bonaventura Cavalieri (vers 1598 – 1647) et fait partie de l’ancêtre du calcul infinitésimal.
L’Harmonie du monde
La tâche principale de Kepler en tant que mathématicien impérial était d’écrire des tables astronomiques, basées sur les observations de Tycho, mais ce qu’il voulait vraiment faire était d’écrire L’Harmonie du monde, prévue depuis 1599 comme un développement de son Mystère du Cosmos. Ce deuxième ouvrage sur la cosmologie (Harmonices mundi libri V Ⓣ, Linz, 1619) présente un modèle mathématique plus élaboré que le précédent, bien que les polyèdres soient toujours là. Les mathématiques de cet ouvrage comprennent le premier traitement systématique des tessellations, une preuve qu’il n’existe que treize polyèdres uniformes convexes (les solides d’Archimède) et le premier compte rendu de deux polyèdres réguliers non convexes (tous dans le livre 2). L’Harmonie du monde contient également ce que l’on appelle aujourd’hui la « troisième loi de Kepler », selon laquelle, pour deux planètes quelconques, le rapport des carrés de leurs périodes sera le même que le rapport des cubes des rayons moyens de leurs orbites. Dès le début, Kepler avait cherché une règle reliant les tailles des orbites aux périodes, mais il n’y a pas eu de lente série de pas vers cette loi comme il y en a eu vers les deux autres. En fait, bien que la troisième loi joue un rôle important dans certaines des dernières sections de la version imprimée de l’Harmonie du monde, elle n’a été découverte qu’une fois l’ouvrage sous presse. Kepler a procédé à des révisions de dernière minute. Il raconte lui-même l’histoire du succès final :
…et si vous voulez le moment exact dans le temps, elle a été conçue mentalement le 8 mars de cette année mille six cent dix-huit, mais soumise au calcul d’une manière malheureuse, et par conséquent rejetée comme fausse, et finalement revenant le 15 mai et adoptant une nouvelle ligne d’attaque, a pris d’assaut les ténèbres de mon esprit. L’appui de la combinaison de mon travail de dix-sept ans sur les observations de Brahe et de la présente étude, qui ont conspiré ensemble, était si fort que j’ai cru d’abord que je rêvais, et que je supposais ma conclusion parmi mes prémisses de base. Mais il est absolument certain et exact que « la proportion entre les temps périodiques de deux planètes quelconques est précisément la proportion sesquialtérée de leurs distances moyennes… »
(Harmonice mundi Livre 5, chapitre 3, trad. Aiton, Duncan et Field, p. 411).
Procès de sorcellerie
Alors que Kepler travaille à son Harmonie du monde, sa mère est accusée de sorcellerie. Il sollicite l’aide de la faculté de droit de Tübingen. Katharina Kepler est finalement libérée, au moins en partie à la suite d’objections techniques découlant du fait que les autorités n’ont pas suivi les procédures légales correctes pour l’utilisation de la torture. Les documents qui subsistent font froid dans le dos. Cependant, Kepler continue à travailler. Dans la diligence, lors de son voyage vers le Wurtemberg pour défendre sa mère, il lit un ouvrage sur la théorie de la musique de Vincenzo Galilei (vers 1520 – 1591, le père de Galilée), auquel il est fait de nombreuses références dans L’Harmonie du monde.
Tables astronomiques
Le calcul des tables, activité normale pour un astronome, a toujours impliqué une arithmétique lourde. Kepler est donc ravi lorsqu’il découvre en 1616 les travaux de Napier sur les logarithmes (publiés en 1614). Cependant, Mästlin lui dit rapidement, d’une part, qu’il est inconvenant pour un mathématicien sérieux de se réjouir d’une simple aide au calcul et, d’autre part, qu’il n’est pas sage de faire confiance aux logarithmes car personne ne comprend leur fonctionnement. (Des commentaires similaires ont été faits à propos des ordinateurs au début des années 1960.) La réponse de Kepler à la deuxième objection a été de publier une preuve du fonctionnement des logarithmes, basée sur une source impeccablement respectable : Le livre 5 des Éléments d’Euclide. Kepler calcule des tables de logarithmes à huit chiffres, qui sont publiées avec les Tables Rudolphes (Ulm, 1628). Les tables astronomiques utilisent non seulement les observations de Tycho, mais aussi les deux premières lois de Kepler. Toutes les tables astronomiques qui utilisaient de nouvelles observations étaient précises pendant les premières années suivant leur publication. Ce qui est remarquable avec les tables de Rudolphine, c’est qu’elles ont prouvé leur précision pendant des décennies. Et au fil des années, la précision continue des tables a naturellement été considérée comme un argument en faveur de l’exactitude des lois de Kepler, et donc de l’exactitude de l’astronomie héliocentrique. L’accomplissement par Kepler de sa morne tâche officielle de mathématicien impérial a conduit à la réalisation de son souhait le plus cher, celui de contribuer à l’établissement du copernicanisme.
Wallenstein
Au moment où les Tables Rudolphes sont publiées, Kepler ne travaille en fait plus pour l’empereur (il a quitté Linz en 1626), mais pour Albrecht von Wallenstein (1583 – 1632), l’un des rares chefs militaires ayant réussi dans la guerre de Trente Ans (1618 – 1648).
Wallenstein, comme l’empereur Rodolphe, attend de Kepler qu’il lui donne des conseils basés sur l’astrologie. Kepler doit naturellement obéir, mais souligne à plusieurs reprises qu’il ne croit pas que des prédictions précises puissent être faites. Comme la plupart des gens de l’époque, Kepler accepte le principe de l’astrologie, selon lequel les corps célestes peuvent influencer ce qui se passe sur Terre (les exemples les plus clairs étant le Soleil qui provoque les saisons et la Lune les marées), mais en tant que copernicien, il ne croit pas à la réalité physique des constellations. Son astrologie était basée uniquement sur les angles entre les positions des corps célestes (« aspects astrologiques »). Il exprime un mépris total pour les systèmes compliqués de l’astrologie conventionnelle.
Décès
Kepler meurt à Ratisbonne, après une courte maladie. Il séjournait dans la ville alors qu’il était en route pour récupérer des sommes qui lui étaient dues dans le cadre des Tables Rudolphines. Il fut enterré dans l’église locale, mais celle-ci fut détruite au cours de la guerre de Trente Ans et il ne reste rien de la tombe.
Note historiographique
On a parfois fait grand cas d’éléments supposés non rationnels dans l’activité scientifique de Kepler. Les astrologues croyants prétendent fréquemment que ses travaux fournissent un antécédent scientifiquement respectable aux leurs. Dans son influent ouvrage Sleepwalkers, le regretté Arthur Koestler a fait de la bataille de Kepler avec Mars un argument en faveur de l’irrationalité inhérente à la science moderne. Il y a eu de nombreux adeptes tacites de ces deux persuasions. Toutes deux sont cependant fondées sur une lecture très partielle de l’œuvre de Kepler. En particulier, Koestler semble ne pas avoir eu l’expertise mathématique nécessaire pour comprendre les procédures de Kepler. Une étude plus approfondie montre que Koestler s’est tout simplement trompé dans son évaluation.
L’élément non rationnel vraiment important dans l’œuvre de Kepler est son christianisme. L’utilisation extensive et réussie des mathématiques par Kepler donne à son travail une apparence « moderne », mais nous avons en fait affaire à un philosophe naturel chrétien, pour qui comprendre la nature de l’Univers incluait la compréhension de la nature de son Créateur.