
Le piante possono far crescere nuove cellule a spirale, come il modello di semi in questo bellissimo girasole.
La spirale avviene naturalmente perché ogni nuova cellula si forma dopo un giro.
“Nuova cellula, poi gira,
poi un’altra cellula, poi gira, …”
Quanto lontano girare?
Quindi, se tu fossi una pianta, quanto gireresti tra una cella e l’altra?
Se non girassi affatto, otterresti una linea retta.
![]()
Ma questo è un design molto povero… vuoi qualcosa di rotondo che si tenga insieme senza spazi vuoti.
Perché non provi a trovare il valore migliore per te?
Prova diversi valori, come 0,75, 0,9, 3,1416, 0,62, ecc.
Ricorda, stai cercando di fare uno schema senza spazi vuoti dall’inizio alla fine:
(A proposito, non importa la parte del numero intero, come 1. o 5. perché sono giri completi che ci riportano nella stessa direzione.)
Che cosa hai ottenuto?
Se hai ottenuto qualcosa che finisce come 0,618 (o 0,382, che è 1 – 0,618) allora “Congratulazioni, sei un membro di successo del regno vegetale!”
 |
Questo perché il Rapporto Aureo (1.61803…) è la soluzione migliore, e il Girasole l’ha scoperto nel suo modo naturale. Prova… dovrebbe apparire così. |
Perché?
Qualunque numero che sia una frazione semplice (esempio: 0.75 è 3/4, e 0,95 è 19/20, ecc), dopo un po’, farà un modello di linee impilate, che crea dei vuoti.
Ma il Rapporto Aureo (il suo simbolo è la lettera greca Phi, mostrato a sinistra) è un esperto nel non essere nessuna frazione.
È un Numero Irrazionale (il che significa che non possiamo scriverlo come una semplice frazione), ma più di questo … è il più lontano che possiamo ottenere dall’essere vicino a qualsiasi frazione.
| Solo essere irrazionale non è abbastanza | |
|---|---|
 |
Pi (3,141592654…), che è anche irrazionale. Purtroppo ha un decimale molto vicino a 1/7 (= 0,142857…), quindi finisce con 7 braccia. |
 |
e (2,71828…) anch’esso irrazionale, non funziona nemmeno perché il suo decimale è vicino a 5/7 (0,714285…), quindi finisce anch’esso con 7 braccia. |
Quindi, come funziona il Rapporto Aureo?
| Una delle proprietà speciali del Rapporto Aureo è che può essere definito in termini di se stesso, come questo: | |
| (In numeri: 1.61803… = 1 + 1/1.61803…) | |
| Che può essere espanso in questa frazione che continua all’infinito (chiamata “frazione continua”): | |
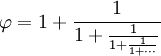 |
|
Quindi, si infila ordinatamente tra le frazioni semplici.
Numeri di Fibonacci
C’è una relazione speciale tra il Rapporto Aureo e i numeri di Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21, … ecc, ogni numero è la somma dei due numeri che lo precedono).
Quando prendiamo due numeri successivi (uno dopo l’altro) di Fibonacci, il loro rapporto è molto vicino al Rapporto Aureo:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Quindi, proprio come otteniamo naturalmente sette braccia quando usiamo 0.142857 (1/7), tendiamo ad ottenere i numeri di Fibonacci quando usiamo il Rapporto Aureo.
Prova a contare i bracci della spirale – le spirali che “girano a sinistra”, e poi le spirali che “girano a destra” … che numeri hai ottenuto?
Crescita a spirale delle foglie

Questo interessante comportamento non si trova solo nei semi di girasole.
Foglie, rami e petali possono anche crescere a spirale.
Perché? In modo che le nuove foglie non blocchino il sole alle foglie più vecchie, o in modo che la massima quantità di pioggia o rugiada venga diretta verso le radici.
In effetti, quando una pianta ha le spirali la rotazione tende ad essere una frazione fatta con due successivi (uno dopo l’altro) numeri di Fibonacci, per esempio:
- Una mezza rotazione è 1/2 (1 e 2 sono numeri di Fibonacci)
- anche 3/5 è comune (entrambi numeri di Fibonacci), e
- 5/8 anche (hai indovinato!)
tutti sempre più vicini al Rapporto Aureo.
|
E per questo i numeri di Fibonacci sono molto comuni nelle piante. Ecco una margherita con 21 petali |
 |
Ma non lo vediamo in tutte le piante, perché la natura ha molti metodi diversi di sopravvivenza.
Angolo d’oro
Finora abbiamo parlato di “giri” (rotazioni complete).
L’equivalente di 0,61803… rotazioni è 222,4922… gradi, o circa 222,5°.
Nell’altra direzione è circa 137,5°, chiamato “angolo d’oro”.
Quindi, la prossima volta che camminate in giardino, cercate l’angolo d’oro,
e contate petali e foglie per trovare i numeri di Fibonacci,
e scoprite quanto sono intelligenti le piante… !
Esercizio
Perché non andate subito nel giardino o nel parco, e cominciate a contare foglie e petali, e a misurare le rotazioni per vedere cosa trovate.
Puoi scrivere i tuoi risultati su questo modulo:
| Nome o descrizione della pianta: | |||
| Le foglie crescono a spirale? S/N | |||
| Conta un gruppo di Foglie: | |||
| Quante foglie (a) ? | |||
| quante rotazioni complete (b) ? | |||
| Rotazione per foglia (b/a) : | |||
| Angolo di rotazione (360 × b/a) : | |||
| Ci sono fiori? Y / N | |||
| Quanti petali sul Fiore 1: | |||
| Fiore 2: | |||
| Fiore 3: | |||
(Ma ricordate, la natura ha le sue regole, e non deve seguire schemi matematici,
ma quando lo fa è fantastico da vedere.)
* Note sull’animazione
I semi di girasole crescono dal centro verso l’esterno, ma nell’animazione ho trovato più facile disegnare prima i semi più giovani e aggiungere quelli più vecchi.
L’animazione dovrebbe continuare più a lungo per essere la stessa del girasole – questo risulterebbe in 55 spirali in senso orario e 34 in senso antiorario (numeri di Fibonacci successivi). Non volevo che ci volesse troppo tempo.
Le spirali non sono programmate in esso – si verificano naturalmente come risultato del tentativo di posizionare i semi il più vicino possibile l’uno all’altro pur mantenendoli alla rotazione corretta.

