Selection Sort – Algoritmo, código fuente, complejidad temporal

Este artículo forma parte de la serie «Algoritmos de ordenación: Ultimate Guide» y…

• describe cómo funciona Selection Sort,
• incluye el código fuente de Java para Selection Sort,
• muestra cómo derivar su complejidad temporal (sin matemáticas complicadas)
• y comprueba si el rendimiento de la implementación de Java coincide con el comportamiento esperado en tiempo de ejecución.

Puedes encontrar el código fuente de toda la serie de artículos en mi repositorio de GitHub.

Ejemplo: Ordenar naipes

Ordenar naipes en la mano es el ejemplo clásico para la Ordenación por Inserción.

La Ordenación por Selección también se puede ilustrar con naipes. No conozco a nadie que recoja sus cartas de esta manera, pero como ejemplo, funciona bastante bien 😉

Primero, pones todas tus cartas boca arriba en la mesa delante de ti. Buscas la carta más pequeña y la llevas a la izquierda de tu mano. Luego buscas la siguiente carta más grande y la colocas a la derecha de la carta más pequeña, y así sucesivamente hasta que finalmente coges la carta más grande en el extremo derecho.

Diferencia con la Ordenación por Inserción

Con la Ordenación por Inserción, tomamos la siguiente carta no ordenada y la insertamos en la posición correcta en las cartas ordenadas.

La Ordenación por Selección funciona más o menos al revés: Seleccionamos la carta más pequeña de las no ordenadas y luego -una tras otra- la añadimos a las cartas ya ordenadas.

Algoritmo de ordenación por selección

El algoritmo se puede explicar de forma más sencilla con un ejemplo. En los siguientes pasos, muestro cómo ordenar el array con Selection Sort:

Paso 1

Dividimos el array en una parte izquierda, ordenada, y una parte derecha, sin ordenar. La parte ordenada está vacía al principio:

Paso 2

Buscamos el elemento más pequeño en la parte derecha, no ordenada. Para ello, primero recordamos el primer elemento, que es el 6. Pasamos al siguiente campo, donde encontramos un elemento aún más pequeño en el 2. Recorremos el resto del array, buscando un elemento aún más pequeño. Como no encontramos ninguno, nos quedamos con el 2. Lo colocamos en la posición correcta intercambiándolo con el elemento del primer campo. Luego movemos el borde entre las secciones del array un campo a la derecha:

Paso 3

Buscamos de nuevo en la parte derecha, sin ordenar, el elemento más pequeño. Esta vez es el 3; lo cambiamos por el elemento de la segunda posición:

Paso 4

Volvemos a buscar el elemento más pequeño en la parte derecha. Es el 4, que ya está en la posición correcta. Así que no hay necesidad de la operación de intercambio en este paso, y sólo mover el borde de la sección:

Paso 5

Como el elemento más pequeño, encontramos el 6. Lo intercambiamos con el elemento del principio de la parte derecha, el 9:

Paso 6

De los dos elementos restantes, el 7 es el más pequeño. Lo cambiamos por el 9:

Algoritmo terminado

El último elemento es automáticamente el mayor y, por tanto, está en la posición correcta. El algoritmo ha terminado, y los elementos están ordenados:

Código fuente Java del Ordenamiento por Selección

En esta sección, encontrarás una implementación sencilla en Java del Ordenamiento por Selección.

El bucle exterior itera sobre los elementos a ordenar, y termina después del penúltimo elemento. Cuando este elemento se ordena, el último elemento se ordena automáticamente también. La variable de bucle i siempre apunta al primer elemento de la parte derecha, no ordenada.

En cada ciclo de bucle, el primer elemento de la parte derecha se asume inicialmente como el elemento más pequeño min; su posición se almacena en minPos.

El bucle interno itera entonces desde el segundo elemento de la parte derecha hasta su final y reasigna min y minPos cada vez que se encuentra un elemento aún más pequeño.

Una vez completado el bucle interno, se intercambian los elementos de las posiciones i (inicio de la parte derecha) y minPos (a menos que sean el mismo elemento).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

El código mostrado difiere de la clase SelectionSort del repositorio de GitHub en que implementa la interfaz SortAlgorithm para ser fácilmente intercambiable dentro del marco de pruebas.

Complejidad temporal de Selection Sort

Denotemos con n el número de elementos, en nuestro ejemplo n = 6.

Los dos bucles anidados son una indicación de que estamos ante una complejidad temporal* de O(n²). Este será el caso si ambos bucles iteran hasta un valor que aumenta linealmente con n.

Es obviamente el caso del bucle exterior: cuenta hasta n-1.

¿Qué pasa con el bucle interior?

Mira la siguiente ilustración:

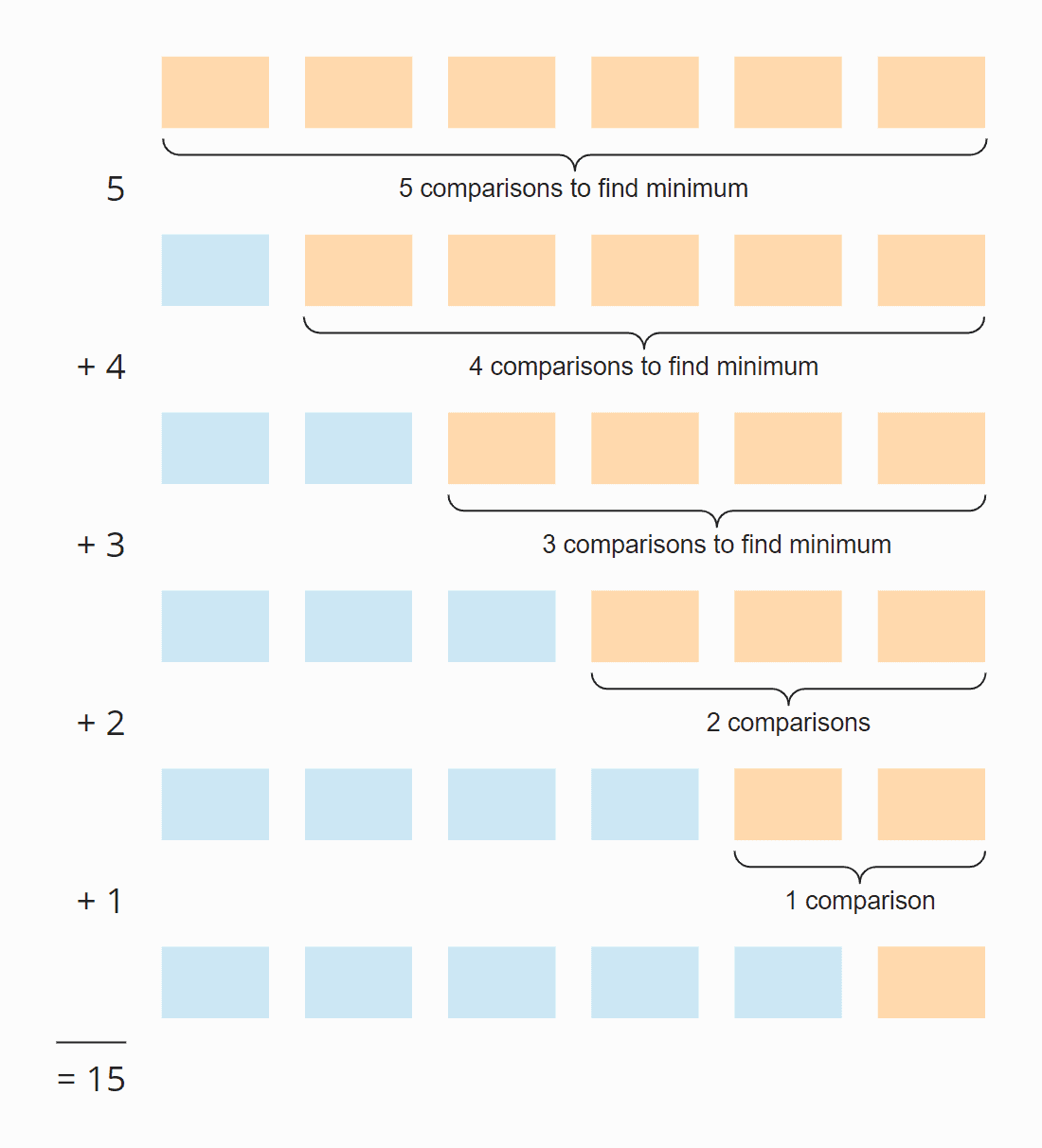
En cada paso, el número de comparaciones es uno menos que el número de elementos sin ordenar. En total, hay 15 comparaciones – independientemente de si el array está inicialmente ordenado o no.

También se puede calcular de la siguiente manera:

Seis elementos por cinco pasos; dividido por dos, ya que en promedio sobre todos los pasos, la mitad de los elementos están todavía sin ordenar:

6 × 5 × ½ = 30 × ½ = 15

Si sustituimos 6 por n, obtenemos

n × (n – 1) × ½

Cuando se multiplica, es:

½ n² – ½ n

La mayor potencia de n en este término es n². La complejidad de tiempo para buscar el elemento más pequeño es, por tanto, O(n²) – también llamado «tiempo cuadrático».

Veamos ahora el intercambio de los elementos. En cada paso (excepto el último), se intercambia un elemento o ninguno, dependiendo de si el elemento más pequeño ya está en la posición correcta o no. Por lo tanto, tenemos, en suma, un máximo de n-1 operaciones de intercambio, es decir, la complejidad de tiempo de O(n) – también llamado «tiempo lineal».

Para la complejidad total, sólo la clase de mayor complejidad importa, por lo tanto:

La complejidad de tiempo promedio, en el mejor de los casos, y en el peor de los casos de Selection Sort es: O(n²)

* Los términos «complejidad temporal» y «O-notación» se explican en este artículo mediante ejemplos y diagramas.

Tiempo de ejecución del ejemplo de ordenación por selección en Java

¡Basta de teoría! He escrito un programa de prueba que mide el tiempo de ejecución de Selection Sort (y de todos los demás algoritmos de ordenación tratados en esta serie) de la siguiente manera:

• El número de elementos a ordenar se duplica después de cada iteración desde los 1.024 elementos iniciales hasta los 536.870.912 (= 229) elementos. Un array del doble de este tamaño no puede crearse en Java.
• Si una prueba tarda más de 20 segundos, el array no se amplía más.
• Todas las pruebas se ejecutan con elementos preordenados tanto ascendentes como descendentes.
• Permitimos que el compilador HotSpot optimice el código con dos rondas de calentamiento. Después, las pruebas se repiten hasta que se aborta el proceso.

Después de cada iteración, el programa imprime la mediana de todos los resultados de las mediciones anteriores.

Aquí está el resultado de la Ordenación por Selección después de 50 iteraciones (en aras de la claridad, esto es sólo un extracto; el resultado completo se puede encontrar aquí):

n	sin ordenar	ascendente	descendente
…	…	…	…
16,384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Aquí las mediciones una vez más en forma de diagrama (en el que he mostrado «sin clasificar» y «ascendente» como una sola curva debido a los valores casi idénticos):

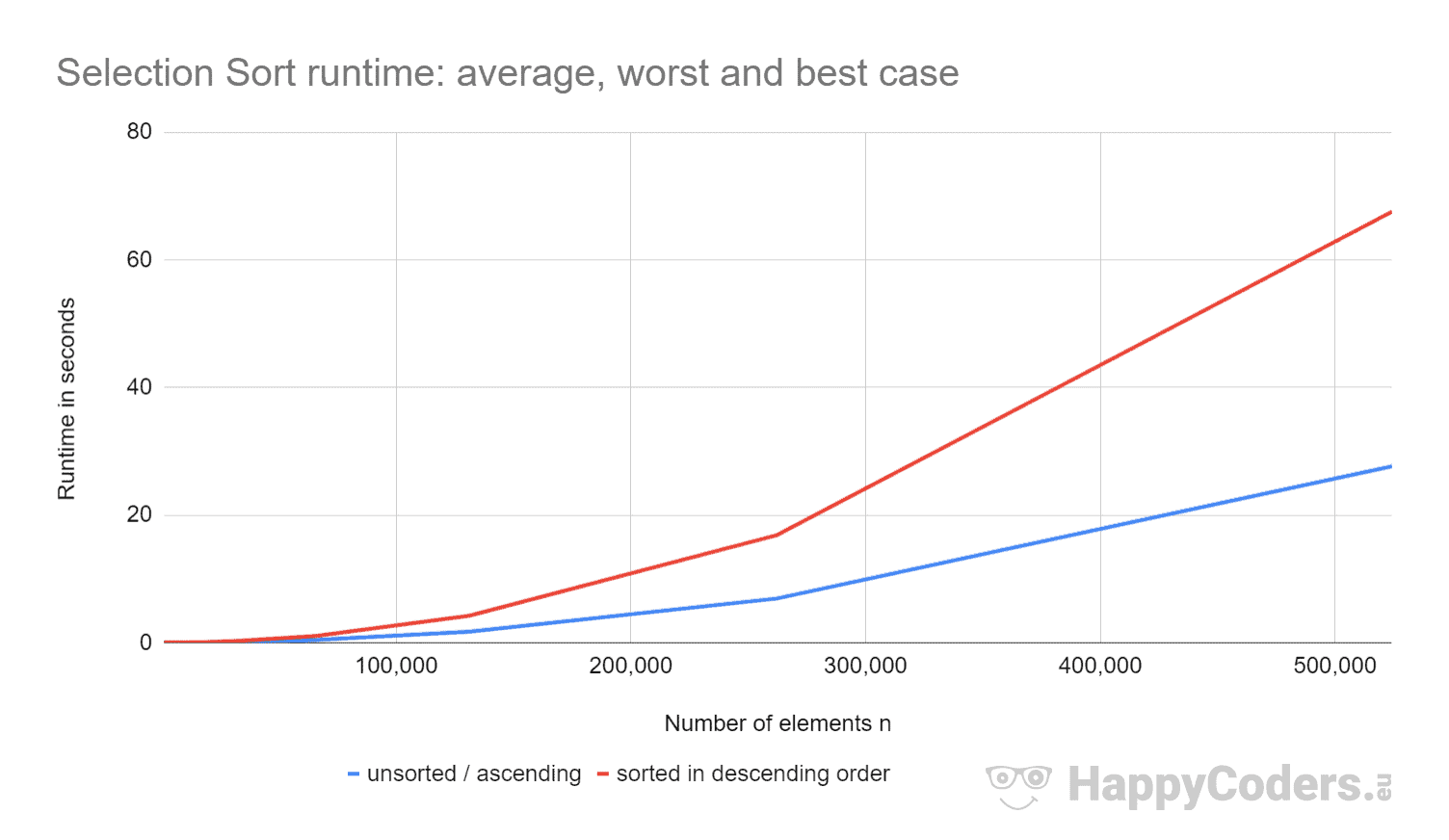
Es bueno ver que

• si se duplica el número de elementos, el tiempo de ejecución se cuadruplica aproximadamente – independientemente de si los elementos están previamente ordenados o no. Esto corresponde a la complejidad de tiempo esperada de O(n²).
• que el tiempo de ejecución para elementos ordenados ascendentes es ligeramente mejor que para elementos no ordenados. Esto se debe a que las operaciones de intercambio, que – como se analizó anteriormente – son de poca importancia, no son necesarias aquí.
• que el tiempo de ejecución para los elementos ordenados descendentes es significativamente peor que para los elementos sin ordenar.

¿Por qué es eso?

Análisis del peor caso de tiempo de ejecución

Teóricamente, la búsqueda del elemento más pequeño siempre debe tomar la misma cantidad de tiempo, independientemente de la situación inicial. Y las operaciones de intercambio sólo deberían ser un poco más para los elementos ordenados en orden descendente (para los elementos ordenados en orden descendente, cada elemento tendría que ser intercambiado; para los elementos no ordenados, casi cada elemento tendría que ser intercambiado).

Usando el programa CountOperations de mi repositorio de GitHub, podemos ver el número de varias operaciones. Aquí están los resultados para los elementos no ordenados y los elementos ordenados en orden descendente, resumidos en una tabla:

n	Comparaciones	Swaps sin ordenar	Swaps descendentes	minPos/min sin clasificar	minPos/min descendente
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

De los valores medidos se desprende:

• Con los elementos ordenados de forma descendente, tenemos -como era de esperar- tantas operaciones de comparación como con los elementos sin ordenar, es decir, n × (n-1) / 2.
• Con elementos sin ordenar, tenemos -como se supone- casi tantas operaciones de intercambio como elementos: por ejemplo, con 4.096 elementos sin ordenar, hay 4.084 operaciones de intercambio. Estos números cambian aleatoriamente de una prueba a otra.
• Sin embargo, con los elementos ordenados de forma descendente, ¡sólo tenemos la mitad de operaciones de intercambio que de elementos! Esto se debe a que, al intercambiar, no sólo ponemos el elemento más pequeño en el lugar correcto, sino también el respectivo compañero de intercambio.

Con ocho elementos, por ejemplo, tenemos cuatro operaciones de intercambio. En las cuatro primeras iteraciones, tenemos una cada una y en las iteraciones cinco a ocho, ninguna (sin embargo el algoritmo sigue funcionando hasta el final):

Además, podemos leer en las mediciones:

• La razón por la que Selection Sort es mucho más lento con elementos ordenados de forma descendente se encuentra en el número de asignaciones de variables locales (minPos y min) al buscar el elemento más pequeño. Mientras que con 8.192 elementos sin ordenar, tenemos 69.378 de estas asignaciones, con los elementos ordenados en orden descendente, hay 16.785.407 asignaciones de este tipo – ¡eso es 242 veces más!

¿Por qué esta enorme diferencia?

Análisis del tiempo de ejecución de la búsqueda del elemento más pequeño

Para los elementos ordenados en orden descendente, el orden de magnitud se puede derivar de la ilustración anterior. La búsqueda del elemento más pequeño se limita al triángulo de las cajas naranja y naranja-azul. En la parte superior naranja, los números de cada caja se hacen más pequeños; en la parte derecha naranja-azul, los números vuelven a aumentar.

Las operaciones de asignación tienen lugar en cada caja naranja y en la primera de las cajas naranja-azul. El número de operaciones de asignación para minPos y min es, pues, en sentido figurado, aproximadamente «un cuarto del cuadrado» – matemáticamente y con precisión, es ¼ n² + n – 1.

Para los elementos no ordenados, tendríamos que penetrar mucho más en la cuestión. Eso no sólo iría más allá del alcance de este artículo, sino de todo el blog.

Por lo tanto, limito mi análisis a un pequeño programa de demostración que mide cuántas asignaciones minPos/min hay cuando se busca el elemento más pequeño en un array no ordenado. Aquí están los valores medios después de 100 iteraciones (un pequeño extracto; los resultados completos se pueden encontrar aquí):

n	número medio de asignaciones minPos/min
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Aquí como diagrama con eje x logarítmico:

El gráfico muestra muy bien que tenemos un crecimiento logarítmico, es decir, con cada duplicación del número de elementos, el número de asignaciones aumenta sólo en un valor constante. Como he dicho, no voy a profundizar en los fundamentos matemáticos.

Esta es la razón por la que estas asignaciones minPos/min tienen poca importancia en los arrays no ordenados.

Otras características de Selection Sort

En las siguientes secciones, hablaré de la complejidad espacial, la estabilidad y la paralelizabilidad de Selection Sort.

Complejidad espacial de Selection Sort

La complejidad espacial de Selection Sort es constante ya que no necesitamos ningún espacio de memoria adicional aparte de las variables de bucle i y j y las variables auxiliares length, minPos y min.

Es decir, no importa cuántos elementos ordenemos -diez o diez millones- sólo necesitamos estas cinco variables adicionales. Observamos que el tiempo constante es O(1).

Estabilidad de la ordenación por selección

La ordenación por selección parece estable a primera vista: Si la parte no ordenada contiene varios elementos con la misma clave, el primero debe ser anexado a la parte ordenada primero.

Pero las apariencias son engañosas. Porque al intercambiar dos elementos en el segundo subpaso del algoritmo, puede ocurrir que ciertos elementos de la parte no ordenada dejen de tener el orden original. Esto, a su vez, lleva a que ya no aparezcan en el orden original en la parte ordenada.

Un ejemplo se puede construir de forma muy sencilla. Supongamos que tenemos dos elementos diferentes con clave 2 y uno con clave 1, ordenados de la siguiente manera, y que los ordenamos con Selection Sort:

En el primer paso, se intercambian el primer y el último elemento. Así, el elemento «DOS» termina detrás del elemento «dos» – el orden de ambos elementos se intercambia.

En el segundo paso, el algoritmo compara los dos elementos posteriores. Ambos tienen la misma clave, 2. Así que no se intercambia ningún elemento.

En el tercer paso, sólo queda un elemento; éste se considera automáticamente ordenado.

Los dos elementos con la clave 2 han sido así intercambiados a su orden inicial – el algoritmo es inestable.

Variante estable de la ordenación por selección

La ordenación por selección puede hacerse estable no intercambiando el elemento más pequeño con el primero en el paso dos, sino desplazando todos los elementos entre el primero y el más pequeño una posición a la derecha e insertando el elemento más pequeño al principio.

Aunque la complejidad temporal seguirá siendo la misma debido a este cambio, los desplazamientos adicionales provocarán una degradación significativa del rendimiento, al menos cuando ordenemos un array.

Con una lista enlazada, cortar y pegar el elemento a ordenar podría hacerse sin ninguna pérdida de rendimiento significativa.

Paralelizabilidad de la ordenación por selección

No podemos paralelizar el bucle exterior porque cambia el contenido del array en cada iteración.

El bucle interior (búsqueda del elemento más pequeño) se puede paralelizar dividiendo el array, buscando el elemento más pequeño de cada subarray en paralelo, y fusionando los resultados intermedios.

Ordenación por selección frente a ordenación por inserción

¿Qué algoritmo es más rápido, la ordenación por selección o la ordenación por inserción?

Comparemos las medidas de mis implementaciones en Java.

Olvido el mejor caso. Con Insertion Sort, la complejidad de tiempo en el mejor caso es O(n) y tomó menos de un milisegundo para hasta 524,288 elementos. Así que en el mejor caso, Insertion Sort es, para cualquier número de elementos, órdenes de magnitud más rápido que Selection Sort.

n	Ordenación por selección sin clasificar	Ordenación por inserción sin clasificar	Ordenación por selección descendente	Ordenación por inserción descendente
…	…	…	…	…
16,384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65,536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

Y de nuevo como diagrama:

El Ordenamiento por Inserción es, por tanto, no sólo más rápido que el Ordenamiento por Selección en el mejor caso, sino también en el caso medio y en el peor.

La razón de esto es que el Ordenamiento por Inserción requiere, de media, la mitad de comparaciones. Como recordatorio, con Insertion Sort, tenemos comparaciones y desplazamientos que promedian hasta la mitad de los elementos ordenados; con Selection Sort, tenemos que buscar el elemento más pequeño en todos los elementos no ordenados en cada paso.

Selection Sort tiene significativamente menos operaciones de escritura, por lo que Selection Sort puede ser más rápido cuando las operaciones de escritura son caras. Este no es el caso de las escrituras secuenciales en matrices, ya que éstas se realizan principalmente en la caché de la CPU.

En la práctica, el Ordenamiento por Selección, por lo tanto, casi nunca se utiliza.

Resumen

El Ordenamiento por Selección es un algoritmo de ordenación fácil de implementar, y en su implementación típica inestable, con una complejidad de tiempo media, en el mejor de los casos y en el peor de los casos de O(n²).

Selection Sort es más lento que Insertion Sort, por lo que rara vez se utiliza en la práctica.

Encontrarás más algoritmos de ordenación en esta visión general de todos los algoritmos de ordenación y sus características en la primera parte de la serie de artículos.

Si te ha gustado el artículo, no dudes en compartirlo utilizando uno de los botones de compartir del final. ¿Quiere que le informe por correo electrónico cuando publique un nuevo artículo? Entonces utiliza el siguiente formulario para suscribirte a mi boletín.