Una ecuación en la forma pendiente-intercepto se escribe como
$y=mx+b$$
Donde m es la pendiente de la recta y b es la intersección y. Puedes utilizar esta ecuación para escribir una ecuación si conoces la pendiente y la intersección y.
Ejemplo
Encuentra la ecuación de la recta
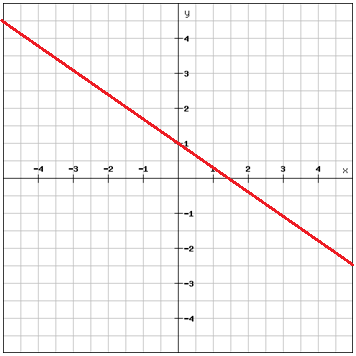
Elige dos puntos que estén sobre la recta
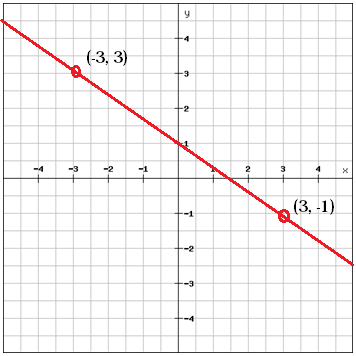
Calcula la pendiente entre los dos puntos
$$m=\frac{y_{2}\, -y_{1}{x_{2}\, -x_{1}}=\frac{{Izquierda (-1 \ derecha )-3}{3-izquierda ( -3 \ derecha )}=\frac{-4}{6}=\frac{-2}{3}$
Podemos encontrar el valor b, la intersección y, mirando la gráfica
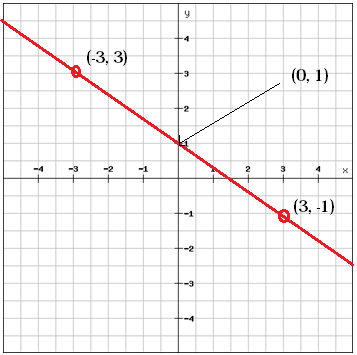
b = 1
Tenemos un valor para m y un valor para b. Esto nos da la función lineal
$$y=-\frac{2}{3}x+1$$
En muchos casos el valor de b no es tan fácil de leer. En esos casos, o si no estás seguro de si la línea realmente cruza el eje y en este punto en particular, puedes calcular b resolviendo la ecuación para b y luego sustituyendo x e y con uno de tus dos puntos.
Podemos usar el ejemplo anterior para ilustrar esto. Tenemos los dos puntos (-3, 3) y (3, -1). A partir de estos dos puntos calculamos la pendiente
$m=-\frac{2}{3}$
Esto nos da la ecuación
$$y=-\frac{2}{3}x+b$$
A partir de esto podemos resolver la ecuación para b
$$b=y+\frac{2}{3}x$$
Y si ponemos los valores de nuestro primer punto (-3, 3) obtenemos
$b=3+\frac{2}{3}\cdot \left ( -3 \right )=3+\left ( -2 \right )=1$$
Si ponemos este valor de b en la ecuación obtenemos
$y=-\frac{2}{3}x+1$$
que es la misma ecuación que obtuvimos al leer la intersección y de la gráfica.
Para resumir cómo escribir una ecuación lineal utilizando la forma pendiente-intercepción se
- Identificar la pendiente, m. Esto se puede hacer calculando la pendiente entre dos puntos conocidos de la recta utilizando la fórmula de la pendiente.
- Hallar la intersección y. Esto se puede hacer sustituyendo la pendiente y las coordenadas de un punto (x, y) de la recta en la fórmula pendiente-intercepto y luego resolver para b.
Una vez que tengas tanto m como b puedes simplemente ponerlos en la ecuación en su posición respectiva.
Video lección
Hallar la ecuación de la gráfica
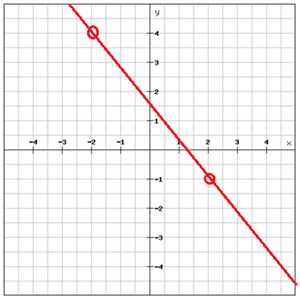
.