Entendiendo las Deducciones de Curvatura
 Publicado: May 26, 2020
Publicado: May 26, 2020
INTRODUCCIÓN
La fabricación de chapa metálica, y específicamente, la fabricación de chapa metálica de precisión es una excelente manera de crear y construir productos robustos mediante procesos de corte, conformación y ensamblaje. Generalmente, los proyectos se diseñan o modelan y luego se envían a los talleres de fabricación para que los liciten y, si los ganan, los fabriquen para imprimirlos. A menudo, las piezas no se diseñan teniendo en cuenta las mejores prácticas de fabricación de chapa metálica, por lo que los talleres de chapa metálica tienen que hacer mucho trabajo entre bastidores, preparando las impresiones para la producción mediante procesos de fabricación estándar. Un tema que rara vez se trata en profundidad y que parece crear la mayor confusión es el de las deducciones de curvatura y, en consecuencia, los márgenes de maniobra.
Deducción de curvatura
Considerar la deducción de curvatura y los márgenes de maniobra es un primer paso fundamental en el diseño de piezas de chapa metálica, ya que afecta a casi todos los pasos siguientes del proceso de fabricación. Además, le permitirá conseguir el tamaño y las dimensiones correctas necesarias en el patrón plano. El patrón plano es el aspecto de la pieza antes de que se produzcan las curvas. Las longitudes en el patrón plano serán diferentes a las del estado doblado. Esto se debe a que el material metálico, cuando se forma en un proceso de doblado, se estira y se comprime dependiendo del grosor y del tipo de material.
La Deducción de Doblado BD se define como la diferencia entre la suma de las longitudes de las bridas (desde el borde hasta el vértice) y la longitud plana inicial. En otras palabras, el material que tendrá que eliminar de la longitud total de las bridas para llegar a la longitud adecuada en el patrón plano. En el ejemplo siguiente, la pieza tiene longitudes de brida de 2″ y 3″ con un radio interior de .250″ a 90° tendrá una longitud de 5″. Cuando se calcula la Deducción de Curvatura encontramos que es igual a .293″ de longitud. Para desarrollar el patrón plano, restaremos .293″ de 5″ para llegar a 4.707″. La imagen de abajo muestra la estrecha relación entre la Deducción de Curvatura y la Asignación de Curvatura.
Fórmula de Deducción de Curvatura
La Fórmula de Deducción de Curvatura tiene en cuenta las geometrías de curvatura y las propiedades de su metal para determinar la Deducción de Curvatura. Los valores que necesitará conocer incluirán el grosor de su material (MT), el ángulo de curvatura (B<), el radio interior (IR) y el factor K (K). Cuando introduzca el espesor del material, utilice la forma decimal en lugar del número de calibre. Para su comodidad, hemos proporcionado una tabla de espesores de material, aquí: Guía de Espesores de Material. Para determinar correctamente el Ángulo de Curvatura debe utilizar el ángulo complementario de la característica de la pieza. Es importante convertir el ángulo incluido en el ángulo complementario antes de realizar el cálculo. El Radio Interior será el radio terminado del ángulo incluido. Por último, el Factor K es una propiedad del sustrato del material que está doblando. Esta propiedad refleja cómo se estira el material cuando se forma.
No se deje intimidar por la longitud de la fórmula para la Deducción de Curvatura. Es larga porque resuelve el repliegue lateral exterior (OSSB) así como la tolerancia de curvatura.
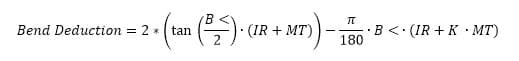 Si el repliegue lateral exterior (OSSB) y la tolerancia de curvatura (BA) están disponibles, entonces la fórmula de deducción de curvatura es considerablemente más corta.
Si el repliegue lateral exterior (OSSB) y la tolerancia de curvatura (BA) están disponibles, entonces la fórmula de deducción de curvatura es considerablemente más corta.
Tabla de deducción de pliegues
La deducción de pliegues puede confundirse fácilmente con la tolerancia de pliegues, por lo que es importante entender la diferencia y cuándo se necesita cada valor. La creación de patrones planos en los dibujos de piezas de chapa metálica resulta fácil una vez que se familiariza con cada uno de estos conceptos. Una de las claves del éxito para acelerar el proceso de búsqueda de estos valores es utilizar una tabla con valores estándar basados en los sustratos y espesores de los materiales. En Meta Fab utilizamos Solid Works, pero existen otros paquetes de software que ayudan a calcular fácilmente la deducción de curvatura o los márgenes de curvatura.
El curvado y conformado de chapa no siempre es igual en cada taller de fabricación. La mayor variación en la fabricación proviene del propio espesor del material. El revestimiento protector, la variación de la aleación y el grosor, así como muchos otros factores, se suman para dar lugar a deducciones de doblado que son exclusivas de sus métodos de procesamiento. La tabla que se muestra a continuación es un buen punto de partida para la mayoría de las aplicaciones de procesamiento de chapa metálica y puede no requerir muchos cambios. Sin embargo, si se dedica a la fabricación de precisión, utilice el archivo de Excel que aparece a continuación e introduzca sus propios datos para adaptarlo a sus operaciones.
La tabla de Excel que aparece a continuación es para los calibres de material pares del 8 al 22 y tiene un factor K por defecto de 0,448 para cada uno. Puede modificar fácilmente el espesor del material, el radio interior y el factor K para cada espesor en la parte superior de cada columna. Esta tabla es sólo para referencia – siempre debe verificar contra su proceso para obtener mejores resultados.
Tabla de Deducción de Curvatura de Chapa (PDF)
Tabla de Deducción de Curvatura de Chapa (Excel)
CONCLUSIÓN
Las Deducciones de Curvatura son los primeros y más críticos aspectos cuando se trabaja con chapa fabricada. Si se omite, causará estragos en sus piezas formadas, si se hace bien, tendrá una medida precisa con la que usted y sus clientes estarán contentos. Esperamos que haya disfrutado de este artículo y lo haya encontrado útil. Vuelva a consultar más artículos sobre las plegadoras y el conformado de chapa metálica.