En la tabla de frecuencias de abajo, encontrarás A = 440 Hz, y luego
A# = 466,16 Hz,
B = 493,88 Hz,
C = 523,25 Hz, etc.
También puedes encontrar Do medio: 261.63 Hz.
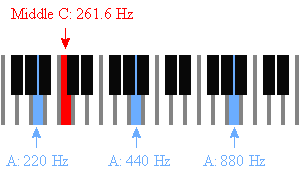
Tabla de frecuencias musicales
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
130.82
138.59
146.83
155.56
164.81
174.61
185
196
207.65
220
233.08
246.94
Nota
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frecuencia
261.63
277.18
293.66
311.13
329.63
349.23
369.99
392
415.3
440
466.16
493.88
Nota
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frecuencia
523.25
554.37
587.33
622.25
659.26
698.46
739.99
783.99
830.61
880
932.33
987.77
Nota
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
C
Frecuencia
1046.5
1108.73
1174.66
1244.51
1318.51
1396.91
1479.98
1567.98
1661.22
1760
1864.66
1975.53
2093.00
Se encuentran utilizando
la frecuencia `= 440×2^(n»/»12)`
para `n = -21, -19, …, 27`
¿De dónde salió esta fórmula?
Este problema me recordó al Interés Compuesto que conocimos antes en Matemáticas del Dinero. La frecuencia tiene que duplicarse cada `12` notas (porque hay `7` notas blancas y `5` notas negras en cada octava.)
Aquí hay una gráfica de esa relación:
Frecuencia `= 440×2^(n»/»12)`
Esta es una curva exponencial, que conocimos antes en Gráficas de Funciones Exponenciales.
Afinación con temperamento igual
Un interesante problema ha enfrentado a los fabricantes de instrumentos musicales durante cientos de años. Para conseguir una «5ª perfecta» (el intervalo entre A y el E anterior, por ejemplo), necesitamos tocar una nota que tenga `1,5` veces la frecuencia de A.
En un violín (o viola o cualquier instrumento de cuerda sin trastes) esto es posible, y podemos tocar un hermoso y perfecto E a `440 × 1,5 = 660\ «Hz»`. Pero fíjese (a partir de la tabla de frecuencias anterior) que un piano que toque la misma nota tocará Mi `= 659,26 «Hz»`.
Hace unos 400 años, los teclados (normalmente clavecines y órganos) se afinaban para un grupo concreto de teclas, de modo que todos los instrumentos, especialmente las cuerdas, sonaban «bien» en esas teclas. El clavicordio sonaba muy bien en esas teclas, pero bastante mal en otras no relacionadas (por ejemplo, si bemol).
En realidad había varios sistemas de afinación diferentes en uso durante la época de Bach, incluyendo meantone (que tenía como objetivo hacer que las terceras mayores sonaran bien, pero no se preocupaba tanto por la calidad de las quintas mayores, con el efecto de que algunas claves no eran utilizables), y la afinación de Werckmeister de 1691 que permitía a los compositores crear música en cualquier clave (con el efecto de que las diferentes claves tenían una calidad tonal diferente).
A principios del siglo XX, se decidió afinar los teclados de manera que las notas estuvieran espaciadas uniformemente (como las frecuencias dadas en la tabla presentada anteriormente). A esto se le llama afinación con temperamento igual. Esta afinación ya se conocía en la época de Bach, pero se rechazó porque se consideraba demasiado «sosa» (todas las teclas tienen la misma calidad de tono) y no existían herramientas de medición de frecuencias que permitieran afinaciones exactas.
Desgraciadamente, la afinación con igual temperamento significa que todos los instrumentos de cuerda tienen que tener en cuenta las ligeras diferencias de afinación entre instrumentos cuando también hay teclados. Las cuerdas suelen ser más felices cuando se tocan sólo con otras cuerdas, por esta razón.
Top
Busca en IntMath
Solver de trigonometría en línea
Este solver de trigonometría puede resolver una amplia gama de problemas de matemáticas.
Ir a: Solucionador de trigonometría en línea