Une équation sous la forme de l’ordonnée à l’origine de la pente s’écrit comme suit
$y=mx+b$$
Où m est la pente de la droite et b est l’ordonnée à l’origine de l’ordonnée. Vous pouvez utiliser cette équation pour écrire une équation si vous connaissez la pente et l’ordonnée à l’origine.
Exemple
Trouver l’équation de la droite
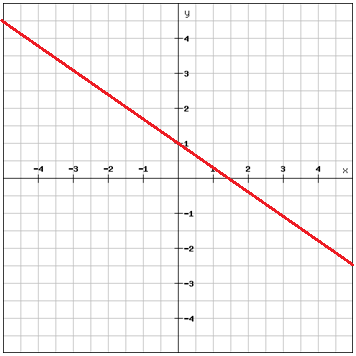
Choisir deux points qui sont sur la droite
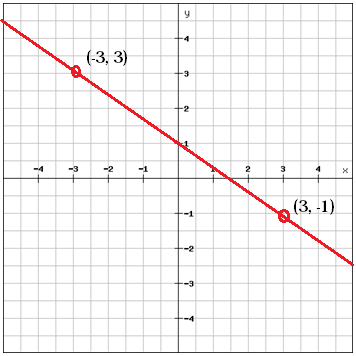
Calculer la pente entre les deux points
$m=\frac{y_{2}\, -y_{1}{x_{2}\, -x_{1}}={\frac{\i}{\i1}gauche (-1{\i}droite )-3}{\i}-{\i}gauche (-3{\i}droite )}={\frac{\i}{\i}-4}{\i}}={\i}2}{\i}3}$
On peut trouver la valeur de b, l’ordonnée à l’origine, en regardant le graphique
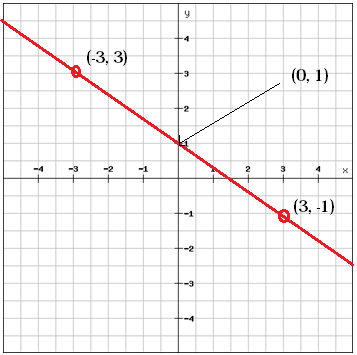
b = 1
Nous avons une valeur pour m et une valeur pour b. Cela nous donne la fonction linéaire
$y=-\frac{2}{3}x+1$$
Dans de nombreux cas, la valeur de b n’est pas aussi facilement lisible. Dans ces cas, ou si vous n’êtes pas sûr que la droite croise réellement l’axe des y en ce point particulier, vous pouvez calculer b en résolvant l’équation pour b et en substituant x et y avec l’un de vos deux points.
Nous pouvons utiliser l’exemple ci-dessus pour illustrer cela. Nous avons les deux points (-3, 3) et (3, -1). A partir de ces deux points, nous avons calculé la pente
$m=-\frac{2}{3}$$
Cela nous donne l’équation
$y=-.\frac{2}{3}x+b$
À partir de là, nous pouvons résoudre l’équation pour b
$b=y+\frac{2}{3}x$
Et si nous mettons les valeurs de notre premier point (-3, 3) on obtient
$b=3+\frac{2}{3}\cdot \left ( -3 \right )=3+\left ( -2 \right )=1$$
Si on met cette valeur pour b dans l’équation on obtient
$y=-\frac{2}{3}x+1$$
C’est la même équation que celle que nous avons obtenue en lisant l’ordonnée à l’origine sur le graphique.
Pour résumer comment écrire une équation linéaire en utilisant la forme pente-interception, vous
- Identifiez la pente, m. Cela peut être fait en calculant la pente entre deux points connus de la ligne en utilisant la formule de la pente.
- Trouvez l’ordonnée à l’origine. Cela peut être fait en substituant la pente et les coordonnées d’un point (x, y) sur la ligne dans la formule de l’ordonnée à l’origine de la pente, puis en résolvant pour b.
Une fois que vous avez à la fois m et b, vous pouvez simplement les mettre dans l’équation à leur position respective.
Leçon vidéo
Trouver l’équation du graphique
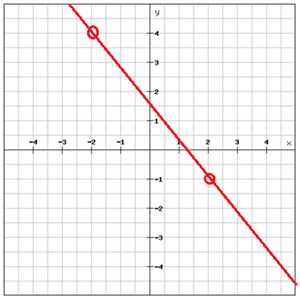
.