Kondensatorns grunder, funktion och olika typer av kondensatorer och deras tillämpningar i kretsar

Kondensatorer – ordet tycks antyda tanken på kapacitet, som enligt ordboken betyder ”förmågan att rymma något”. Det är precis vad en kondensator gör – den håller elektrisk laddning. Men vad gör den till en vanlig komponent i nästan alla elektroniska kretsar? Låt oss bryta ner grejerna bakom kondensatorer för att förstå vad den gör och hur man kan använda dem i den här artikeln.

Vad är en kondensator?

En kondensator i sin mest primitiva form består av två ledande plattor som skiljs åt av ett dielektriskt medium. Termen dielektrikum är bara ett fint ord för en isolator som kan polariseras, dvs. bilda negativa och positiva laddningar på motsatta sidor. När en spänning läggs över dessa två plattor flyter strömmen genom de ledande plattorna. Den ena sidan blir positivt laddad (brist på elektroner) och den andra sidan blir negativt laddad (överskott av elektroner). Vi känner alla till att olikartade laddningar attraherar varandra, så eftersom plattorna är motsatt laddade attraheras laddningarna på plattorna.

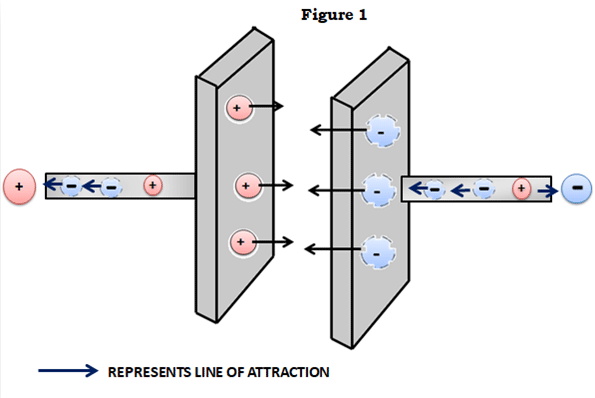
Håll dig i minnet att det finns en isolator mellan plattorna, så laddningarna kan inte ”flöda” för att utjämna varandra och är (i idealfallet) fast i ett tillstånd av ömsesidig attraktion och stannar kvar. Och det är så kondensatorer utför sin mest grundläggande funktion – att behålla eller lagra laddning.

Kondensatorers symbol

Då kondensatorer har två parallella metallplattor som diskuterats ovan, representerar deras symbol på sätt och vis samma sak. Den är åtminstone lätt att rita

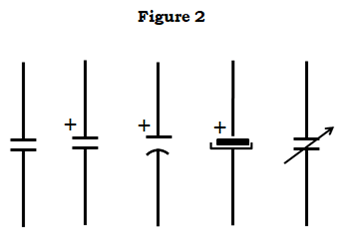
I ett praktiskt fall är kondensatorer inte längre bara två plattor med ett mellanrum mellan dem, när det gäller aluminiumelektrolyter har de två plattorna formen av metallfolie som är upprullad med ett mellanrum mellan dem i ett rör.

Den andra uppsättningen symboler står för polariserade kondensatorer, det vill säga sådana som har definierade positiva och negativa terminaler genom intern konstruktion. Om man råkar vända på dessa terminaler kommer det nästan säkert att resultera i ett spektakulärt misslyckande (särskilt för större exemplar), som kastar ut bitar av folie och pappersmetrar från platsen för misslyckandet och för det mesta luktar mycket illa.

Kapacitans och spänningsklassning för en kondensator

Kondensatorer mäts i Farads; det är uppkallat efter den berömde brittiske elektrokemisten Michael Faraday. Enheten för kapacitans, som står för Coulomb per Volt. Coulomb (uttalas ”koo-lom”) är S.I.-enheten för laddning, och en volt är som bekant enheten för spänning eller potentialskillnad. Farad är alltså den mängd laddning som lagras per volt potentialskillnad. Detta enkla sätt att se matematiskt på en kondensator lämpar sig för ett stort antal tolkningar, som manifesteras av en massa dödligt komplexa matematiska ekvationer, t.ex. integraler, exponenter och vektorer, som vi ingenjörer kommer att använda oss av när vi arbetar med kondensatorer, men det är något som ligger långt utanför den här artikelns räckvidd. Vi kommer dock att gå in på lite intressant matematik som hjälper oss att konstruera kretsar med kondensatorer senare i artikeln

Förvisso är farad (en coulomb per volt) en mycket stor enhet för de flesta praktiska ändamål (eftersom coulomb i sig själv är en ganska stor laddningsmängd, som du kanske redan vet), så de flesta kondensatorer (med undantag för mycket stora kondensatorer) mäts i mikrofarad, eller en miljondel (0,000001) av en farad. Anta att du har en kondensator med texten 25V 10uF (prefixet ”u” står för mikro, det är en förvanskning av den grekiska symbolen µ (”mu”) som betyder ”mikro”) på plastens ytterhölje. Eftersom kapsylen (kort för kondensatorer i elektronikvärlden) är dimensionerad för 10uF kan den hålla en laddning på tio mikrocoulomb (det vill säga tio miljondelar av en coulomb, 0,000010 C) per volt spänning över sina terminaler. Det innebär att kondensatorn vid den maximala spänningen på 25 V kan hålla en laddning på 25 V x 10uF, vilket motsvarar 0,000250 Coulombs.

Håll dig till att jag sa ”maximal” spänning. Maxspänning är förmodligen den viktigaste värderingen på kondensatorn. Den talar om hur mycket spänning kondensatorn kan hantera över sina terminaler innan den går KABOOM………!

Kondensatorns funktion

Vad som händer inne i en kondensator är att isolatorn mellan plattorna genomgår en process som kallas ”dielektrisk nedbrytning”, vilket innebär att isolatorn inte längre kan isolera, eftersom spänningen över isolatorn är för hög för att den ska kunna fortsätta att vara en isolator. Den underliggande fysiken är något oklar, men allt man behöver veta för att förstå varför detta sker är att ingen isolator är perfekt, det vill säga upp till en viss punkt. Även den starkaste bron kollapsar om den överbelastas. Det som händer här är liknande. För att minska nedbrytningen kan man öka avståndet mellan de två plattorna, men det kommer med en motprestation – minskad kapacitans, eftersom plattorna är längre ifrån varandra och laddningarna inte attraheras lika mycket som när de är närmare varandra – ungefär som hur magneter beter sig.

En bra tumregel skulle vara att använda kapslar som är dimensionerade för en 50 % högre spänning än den som din krets kan förväntas uppleva. Detta lämnar en stor säkerhetsmarginal. Om du till exempel behöver en kondensator för att frikoppla (oroa dig inte, frikoppling förklaras senare i artikeln) en 12V strömförsörjningsskena, kan du komma undan med att använda en 16V kondensator, men att använda en 25V kondensator rekommenderas eftersom det ger dig en stor säkerhetsmarginal. Okej, du har kommit på det!! Ja 25V är naturligtvis inte 25 % högre än 12V, men 18V är inte ett standardkondensatorvärde – du kommer inte att hitta någon med den spänningen. Det närmaste är 25V.

Differenta typer av kondensatorer

Anledningen till de olika nedbrytningsspänningsintervallen beror på det material som används som dielektrikum, vilket också är den grund på vilken kondensatorer klassificeras:

Aluminiumelektrolytkondensatorer

Dessa är förmodligen de mest igenkännliga typerna av kondensatorer. De kommer i distinkta metallburkar med ett plasthölje, med tydligt angivna spännings- och kapacitansvärden och ett vitt band för att ange katoden. Namnet kommer från det faktum att ”plattorna”, som nämnts ovan, är gjorda av kemiskt etsad aluminiumfolie. Ätningsprocessen gör aluminiumet poröst (ungefär som en svamp) och ökar dess yta kraftigt, vilket ökar kapacitansen. Det dielektriska materialet är ett tunt lager av aluminiumoxid. Dessa kondensatorer är fyllda med olja som fungerar som en elektrolyt, därav namnet. Elektrolytkondensatorer är polariserade på grund av sin inre konstruktion. De har stor kapacitans jämfört med andra medlemmar av kondensatorfamiljen, men mycket lägre spänningar. Du kan förvänta dig att se elektrolytiska kondensatorer mellan 0,1uF till monster som 100mF och med nominella spänningar på några få volt till omkring 500V. Deras inre motstånd tenderar dock att vara högt.

SIDE NOTE: Det inre motståndet i kondensatorer beror på de material som kapseln är tillverkad av – till exempel motståndet i aluminiumfolien eller motståndet i ledningarna.

Keramiska kondensatorer

Detta är kapslar med ett keramiskt dielektrikum. Eftersom nedbrytningsgränsen för det keramiska dielektrikumet är ganska hög kan du förvänta dig att se keramiska kapslar med galna nedbrytningsspänningar som 10kV. Kapaciteten tenderar dock att vara låg, i storleksordningen picofarads (0,0000000000000001F) till några tiotal mikrofarads. De är i allmänhet mycket mindre än andra typer av kondensatorer, vilket framgår av bilden. De har också mycket små inre resistanser.

Identifiering av keramiska kondensatorer

Värdet på en keramisk kapacitans kommer inte att nämnas direkt på den keramiska kondensatorn. Det kommer alltid att finnas ett tresiffrigt nummer följt av en variabel; låt oss lära oss hur man identifierar värdet med hjälp av dessa nummer. Tänk på följande kondensator:

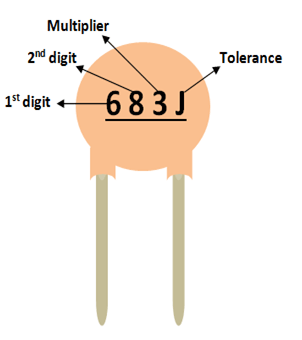
Som du märker är dessa tre siffror uppdelade i två siffror och den tredje siffran är multiplikatorn. I det här fallet är 68 siffran och 3 är multiplikatorn. Så 68 ska multipliceras med 10^3. Enkelt uttryckt är det 68 följt av 3 nollor. Värdet på denna kondensator blir alltså 68000 pF. Observera att enheten alltid ska vara pF. På samma sätt innebär en kondensator med koden 220 att den är 22 Pico farad, eftersom 10^0 är 0.

Kondensatorns spänningsvärde kan hittas genom att använda raden under denna kod. Om det finns en linje så är spänningsvärdet 50/100V om det inte finns någon linje så är det 500V.

De vanligaste kondensatorvärdena tillsammans med deras omräkning i Pico Farad, Nano Farad och mikrofarad ges nedan.

Filmkondensatorer

Som namnet antyder är dielektrikumet i dessa kondensatorer en plastfilm, ofta välkända plaster som mylar och polyester. De har samma egenskaper som keramiska kapslar, höga genombrottsspänningar (på grund av hur plastpolymererna beter sig) och låga kapaciteter. Den enda skillnaden är att de tenderar att vara något större även om de ytligt sett ser ut som keramiska kapslar. Det inre motståndet är jämförbart med keramiska kapslar.

Tantal- och niobkondensatorer

Dessa kapslar faller tekniskt sett under den elektrolytiska kategorin av kondensatorer. Här är elektrolyten ett fast material av tantal- eller nioboxid. De har ett mycket lågt inre motstånd för en given kapacitans, men de är mindre immuna mot överspänning jämfört med andra typer (keramik har bäst) och tenderar att gå sönder utan större förvarning och med en massa otäck svart rök.

Specialkondensatorer för speciella ändamål

Dessa innefattar silver – glimmerkapslar, X- och Y-klassade kapslar, etc. X- och Y-klassade kondensatorer är t.ex. byggda för linjefiltrering – mer robust konstruktion och högre spänningsnivåer, även låga kapaciteter, för att minska strömmen som passerar genom den om växelspänning appliceras och för att begränsa den energi som lagras i kapseln om likspänning appliceras.

Superkondensatorer och ultrakondensatorer

De tar kondensatorer till en helt ny nivå, med kraftigt förhöjda kapaciteter, ibland i storleksordningen hundratals Farad! Detta är möjligt tack vare en del smart kemi. Superkondensatorer och ultrakondensatorer överbryggar klyftan mellan kondensatorer och kemiska batterier. De finns dock i mycket låga spänningar.

Och detta är i stort sett alla vanliga typer av kondensatorer som du vanligtvis kan stöta på i elektronikens värld.

Hur kondensatorer beter sig i kretsar

En användbar första uppgift skulle vara att lära sig att beräkna energilagren i en kondensator, som ges av formeln,

E = 1/2CV2

Varvid E är den lagrade energin i joule, C är kapacitansen i farad och V är spänningen i volt. Observera att denna ekvation tar formen av många andra newtonska ekvationer för energi, ett snyggt påskägg!

Antag att du har en kapsling som är dimensionerad för en spänning på 50V och med en kapacitans på 1000uF, skulle den lagrade energin vid hela 50V vara:

1/2 * 0.001000F * 50V * 50V

Vilket motsvarar ynka 1,25 J lagrad energi.

Detta avslöjar en stor nackdel med kondensatorer som energilagringsenheter – den lagrade energin för en given storlek är mycket låg, ett batteri av samma storlek skulle ha minst tusen gånger mer lagrad energi! Kapslar har dock mycket lägre inre motstånd än kemiska batterier, vilket gör att de snabbt kan dumpa all sin lagrade energi. Om man kortsluter ett batteri skulle det bara värmas upp på grund av den energi som går förlorad på grund av det inre motståndet, men om man kortsluter en kondensator skulle det bara ge upphov till några gnistor eftersom all laddning dumpas på en gång utan att kondensatorn skadas.

För det andra finns det en annan snygg formel som relaterar spänning, ström och kapacitans:

I/C = dV/dt

Varvid I är den ström som tillförs kondensatorn i ampere, C är kapacitansen i farad och dV/dt är förändringshastigheten för spänningen över kondensatorns terminaler. Tänk på detta i termer av dess enhet – volt per sekund för en given ström och kapacitans. Oroa dig inte för det lilla ”d”, det är bara ett matematiskt sätt att säga ”till gränsen noll”.

Säg att du har ett nätaggregat som spottar ut en konstant spänning på 5V vid en konstant ström på 1mA, då kan vi genom att omorganisera ekvationen hitta den tid som det tar att ladda en kondensator på 100uF till 5V:

dt = CdV/I

dt = (0.000100F * 5V)/0,001A

dt = 0,5 sekunder

Så kondensatorn skulle ladda upp till 5V på 0,5 sekunder. (Kom ihåg att en kondensator bara kan ladda upp till den maximala spänning som tillförs den, aldrig mer, de kan inte magiskt ”skapa” spänning.)

Detta förutsägbara beteende hos en kondensator gör den mycket användbar för att generera tidsfördröjningar, till exempel med lite extra kretsar. Du kan ordna om ekvationen för att få fram tid.

Nu kommer de bra sakerna – riktiga kondensatorkretsar!

Kondensatorbeteende i kretsar

Låt oss börja enkelt – de olika sätten som kondensatorer kan kopplas ihop på. Det är ungefär samma sak som att koppla ihop två motstånd – du kan antingen koppla dem i serie eller parallellt.

Kondensatorer i parallellkoppling

Figuren nedan visar tre kondensatorer kopplade i parallellkoppling, med alla respektive positiva och negativa terminaler anslutna tillsammans (förutsatt att kapslarna är polariserade). Den totala kapacitansen i detta arrangemang är helt enkelt summan av alla kapacitanser hos alla kondensatorer i kretsen. Detta är logiskt, eftersom en parallellkoppling av kondensatorplattorna ökar ytan, vilket ökar kapacitansen.

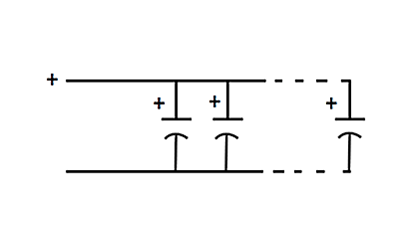
Den maximala spänningen som denna typ av arrangemang kan hantera är spänningen för den minsta kondensatorn, eftersom i spänningen är gemensam för alla kapslar.

Ett exempel bör klargöra detta. Anta att du har två kondensatorer, den ena med värdena 25V 470uF och den andra 35V 1000uF. Den totala kapacitansen skulle vara 470uf + 1000uF = 1470uF. Den maximala spänningen som du kan lägga över denna bank (ett gäng kondensatorer som är sammankopplade kan kallas en kondensatorbank) skulle dock bara vara 25V. Om du sätter något högre än så över denna bank skulle gnistorna flyga, eftersom du överskrider den maximala spänningen för kondensatorn på 25 V.

Kondensatorer i serie

Att koppla kondensatorer parallellt är särskilt användbart när du vill ha en stor kapacitans och du bara har små värden. Genom att sätta ihop dessa kapslar med mindre värden i parallell kommer du så småningom att få det större värdet och göra jobbet, förutsatt att du är uppmärksam på spänningen.

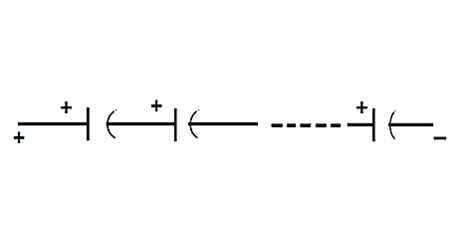
Nu är det lite mer komplicerat att sätta kondensatorer i serie. Kapacitansen ges av formeln:

1/Ctotal = 1/C1 + 1/C2 + … + 1/Cn

Varvid C1, C2…Cn är kapacitanserna för varje kondensator som används i kretsen.

Spänningen som banken nu klarar av är summan av alla märkspänningar.

Om du får en kondensator som är dimensionerad för 10V 1uF och en kondensator som är dimensionerad för 50V 10uF, så är den spänning som banken kan hantera i serie 10V + 50V = 60V. Kapacitansen blir då 0,9091uF.

Kondensatorspänning i förhållande till tiden

Hur blir det om vi vill ladda en kondensator? Vi kan bara koppla den mot en spänningskälla, som i figuren nedan. Vad som skulle hända här är att i det ögonblick spänningskällan ansluts, förutsatt att kondensatorn är helt urladdad, rusar laddningar för att ackumuleras på plattorna, vilket leder till en mycket stor (i teorin oändlig!) strömtopp som endast begränsas av kondensatorns inre motstånd. Detta är naturligtvis inte önskvärt om din strömförsörjning råkar vara något som ett batteri. En förnuftig idé skulle vara att lägga till ett motstånd i serie med kondensatorn och spänningskällan för att begränsa strömmen som i figuren, och voila! Du har något som ingenjörer kallar en RC-krets, ”R” för motstånd och ”C” för kondensator!

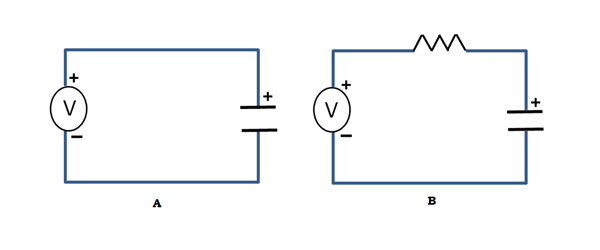
Denna krets visar ett intressant beteende. När spänningen kopplas till den sida av motståndet som är markerad med ”I” stiger spänningen på kondensatorn långsamt eftersom strömmen är begränsad. Grafen ser ut ungefär så här:

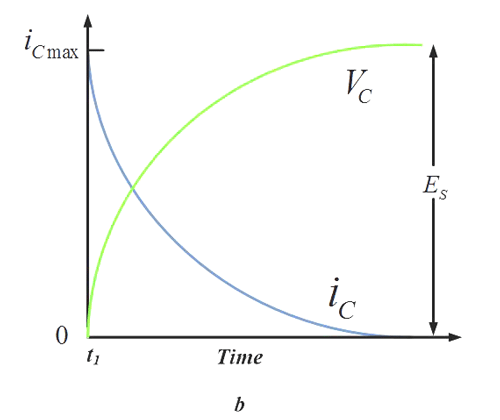
De mer matematiskt lagda av mina tittare skulle känna igen formen på lutningen – den liknar exponentialfunktionens form!

Håller du minnet att jag sa att kapslar kunde användas för att generera tidsfördröjningar? Detta är ett sätt att göra det utan en konstant strömkälla (vilket kräver ytterligare kretsar). Eftersom den tid det tar att nå en viss spänning är förutsägbar om vi känner till kapacitansen, spänningen och motståndet, kan vi skapa tidsfördröjningskretsar.

Produkten av motstånd och kapacitans, RC, är känd som kretsens tidskonstant. Denna parameter blir användbar för att faktiskt bestämma tiden för att nå en viss spänning exakt, vilket framgår av diagramfiguren nedan.

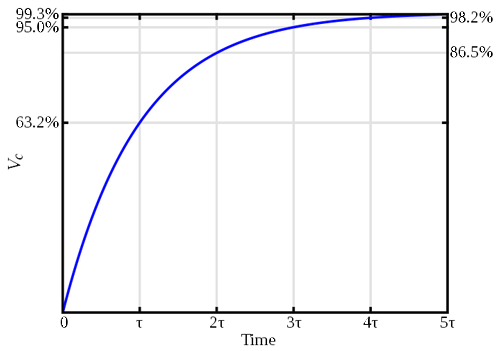
Från diagrammet kan man se att kondensatorn når 63 % av den applicerade spänningen på en tidskonstant, och så vidare.

Detta är den princip som den allsidiga 555-timern använder, även om konstruktionsekvationerna är lite annorlunda.

En annan intressant tillämpning av RC-kretsar är signalfiltrering, dvs. att ta bort en elektrisk signal med en oönskad frekvens från en krets. RC-kretsen tar en given tid på sig att ladda och ladda ur en källa. Om vi applicerar en periodisk våg med en tidsperiod som är större än RC, skulle samma signal visas på utgången med mycket liten förvrängning. När frekvensen ökar fortsätter dock signalen att ändra polaritet snabbare än vad kretsen kan ladda och urladdning, och till slut efter en viss punkt försvinner signalen, och allt du har kvar är ren likström! Detta kallas signaldämpning. Som du kan se fungerar en RC-krets som ett filter som blockerar växelströmssignaler (även sådana som är överlagrade på likström, dvs. som har en likströmsförskjutning) över en viss frekvens. Den här typen av filter kallas lågpassfilter, det vill säga det låter låga frekvenser passera men inte höga frekvenser.

Kondensatorer i växelströmskretsar

Kondensatorer beter sig på ett intressant sätt när de placeras i växelströmskretsar. De kan betraktas som frekvensberoende motstånd, ur signalperspektiv. Som vi sett ovan blockerar RC-kretsen all växelström från en signal, men vad händer när en kondensator kopplas i serie med en växelspänningskälla? Den exakta motsatsen!

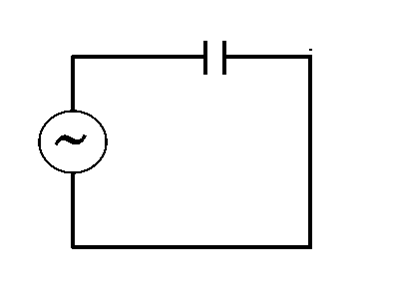
Då kondensatorn bara är två metallplattor som är åtskilda av en isolator, släpper den inte igenom någon likström. En växelströmssignal har dock ständigt skiftande spänningar, så den ena plattan ser en skiftande spänning och inducerar den motsatta laddningen på den andra plattan, enligt figuren:

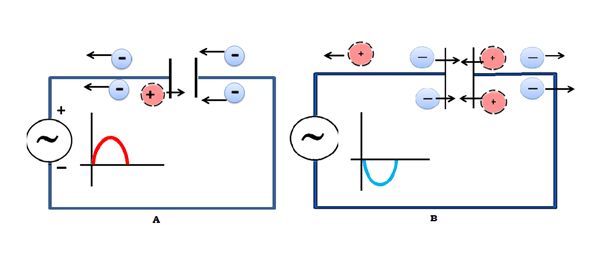
Detta har den övergripande effekten att strömmen kan ”passera” genom kondensatorn vid relativt höga frekvenser. Genom att lägga ett motstånd parallellt med utgången får man ett högpassfilter, dvs. ett filter som endast släpper igenom höga frekvenser och blockerar alla likströmsignaler.

Växelströmsmotståndet eller impedansen för en kondensator ges av formeln:

XC = 1/(2*π*f*C)

Varvid XC är den kapacitiva reaktansen eller impedansen, f är frekvensen och C är kapacitansen. Du kan använda denna formel för att beräkna det virtuella ”motstånd” som en kondensator har i en växelströmskrets.

Var kondensatorer finns i naturen

Okej, det var tillräckligt med teori. Låt oss titta på de många användningsområdena för kondensatorer.

Det första stället man kan förvänta sig att se kondensatorer på är i nätaggregat av alla slag som filter och för frikoppling. De fungerar som laddningsreservoarer och ger snabb ström när belastningen behöver det.

Här är två oscilloskopbilder som visar effekten av att inte ha och att ha en kondensator över ledningarna i ett nätaggregat. Som du kan se minskar kondensatorer dramatiskt ”bruset” på strömförsörjningsskenorna, vilket skyddar känsliga delar från plötsliga spänningsspikar.

De kallas också för ”frikopplingskondensatorer”, eftersom de ”frikopplar” sektioner av den krets över vilken de är monterade från strömförsörjningen. Ibland kan strömledningarna på ett kretskort vara ganska långa och ha en hög induktans och ett högt motstånd. Detta kan leda till att de ger mindre ström än vanligt. Att ha en kondensator i slutet av matarledningen är som att ha ett mindre tillfälligt ”batteri” över enheten, som ger strömstötar när det behövs och laddar upp när enheten förbrukar lite ström.

Du kan använda formeln I/C = dV/dt för att beräkna den nödvändiga kapacitansen för att avlägsna ”rippel”-spänning från matningsterminalerna.

Antag att du har ett nätaggregat vars spänning varierar från 11,5 V till 12 V (rippel) var 10:e sekund, vilket är vanligt i nätverksdrivna apparater på grund av frekvensen 50 Hz, och att du behöver placera en kapsling över terminalerna för att jämna ut spänningen. Om belastningsströmmen i det här fallet är 1A kan vi ordna om formeln på följande sätt för att ta reda på kapaciteten:

(I * dt)/dV

Varvid I är belastningsströmmen, dt är tidsperioden för bruset och dV är rippelspänningen. Genom att ersätta värdena finner vi att vi behöver en kapacitans på 20000uF. Nu kan detta tyckas vara mycket, men du kan komma undan med mycket mindre. Det erhållna värdet tjänar bara som en riktlinje.

I verkligheten kan man hitta flera typer och värden av kondensatorer över kraftledningar, detta för att minska brusinnehållet över många frekvenser och få en så jämn spänning som möjligt.

En annan användning av kondensatorer är i komplicerade filter som detta:

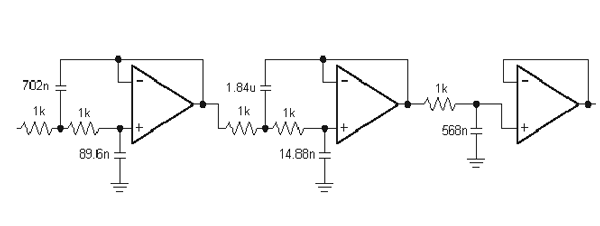
Men ett enklare filter skulle vara RC-filtret, ett intressant filter beskrivs här.

Alla känner till mikrokontrollerkortet Arduino. Ett mångsidigt verktyg, men har du aldrig undrat varför de analoga utgångarna spottar ut en digital PWM-signal? Det beror på att de utformades för att användas tillsammans med ett externt filtreringsnätverk för att jämna ut PWM-spänningen till en verkligt analog spänning. Detta kan göras med så enkla delar som ett 1K motstånd och en 10uF kondensator. Prova det!

En annan användning, som nämns ovan, är timing. En enkel oscillator kan byggas med hjälp av en NAND-port (försök att lista ut varför AND-portar inte fungerar), ett motstånd och en kondensator.

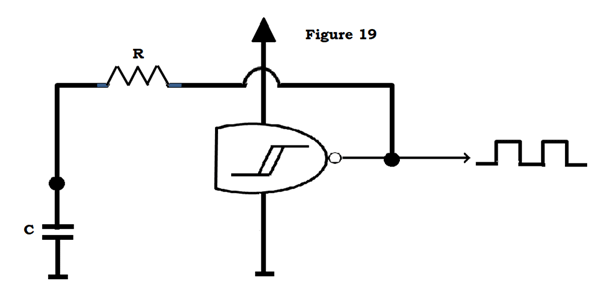
Antagen att det till en början inte finns någon spänning över kondensatorn, ser NAND-ingångarna (som är bundna till varandra) nära 0V över sig, och slår på utgången. Kapsylen laddas nu genom motståndet. När den når grindens ”hög”-tröskel, slår utgången på låg nivå och kapseln laddas nu ur. Denna cykel fortsätter att producera en kvadratisk våg med en frekvens som beror på värdena för R och C.

Enligt en annan intressant användning av kondensatorer är energilagring. Naturligtvis kan kondensatorer inte mäta sig med batterier, men för vissa tillämpningar som behöver energin snabbt är kapslar de bästa för uppgiften.

Enheter som coilguns (mer finns på webben) behöver en stor strömpuls för att accelerera projektilen, så högspänningskondensatorer används för sådana ändamål, ofta med värden som 450V 1500uF, som kan lagra betydande energimängder.