
Plantas podem crescer novas células em espiral, como o padrão de sementes neste belo girassol.
A espiral acontece naturalmente porque cada nova célula é formada após uma volta.
“Nova célula, depois vire,
depois outra célula, depois vire, …”
Quão longe para virar?
Então, se você fosse uma planta, quanto de volta teria entre as novas células?
Se você não virar de todo, você recebe uma linha reta.
![]()
Mas isso é um design muito pobre …… você quer algo redondo que se mantenha junto sem lacunas.
Por que não tentar encontrar o melhor valor para si mesmo?
Tente valores diferentes, como 0,75, 0,9, 3,1416, 0,62, etc.
Lembrar, você está tentando fazer um padrão sem intervalos do início ao fim:
(A propósito, não importa a parte do número inteiro, como 1. ou 5. porque são revoluções completas que nos apontam de volta na mesma direção.)
O que você conseguiu?
Se você conseguiu algo que termina como 0,618 (ou 0,382, que é 1 – 0,618) então “Parabéns, você é um membro bem sucedido do reino vegetal!”
 |
Isso é porque a Razão de Ouro (1.61803…) é a melhor solução, e o Girassol descobriu isto à sua maneira natural. Tenta-o… deve parecer-se com isto. |
Porquê?
Um número que é uma simples fracção (exemplo: 0.75 é 3/4, e 0,95 é 19/20, etc) fará, depois de um tempo, um padrão de linhas empilhadas, o que faz com que as lacunas sejam maiores.
But o Golden Ratio (seu símbolo é a letra grega Phi, mostrada à esquerda) é um especialista em não ser nenhuma fração.
É um Número Irracional (significando que não podemos escrevê-lo como uma simples fração), mas mais do que isso … é o mais longe que podemos chegar de estar perto de qualquer fração.
| Apenas ser irracional não é suficiente | |
|---|---|
 |
Pi (3.141592654…), o que também é irracional. Felizmente tem uma casa decimal muito próxima de 1/7 (= 0,142857…), por isso acaba com 7 braços. |
 |
e (2,71828…)) também irracional, também não funciona porque o seu decimal está próximo de 5/7 (0,714285…), por isso também acaba com 7 braços. |
Então, Como funciona a Golden Ratio?
| Uma das propriedades especiais da Golden Ratio é que ela pode ser definida em termos próprios, assim: | ||
| (Em números: 1.61803… = 1 + 1/1.61803…) | ||
| Que pode ser expandido para esta fração que continua para sempre (chamada “fração contínua”): | ||
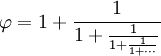 |
||
Então, ele desliza ordenadamente entre frações simples.
Números Fibonacci
Existe uma relação especial entre a Razão de Ouro e os Números Fibonacci (0, 1, 1, 2, 3, 5, 8, 13, 21, … etc, cada número é a soma dos dois números que o precedem).
Quando tomamos qualquer dois números sucessivos (um após o outro) Números Fibonacci, a sua relação é muito próxima da Relação de Ouro:
|
A
|
B
|
B / A
|
|
|---|---|---|---|
|
2
|
>
3
|
1.5 | |
|
3
|
5
|
1.666666666… | |
|
5
|
8
|
1.6 | |
|
8
|
13
|
1.625 | |
|
13
|
21
|
1.615384615… | |
|
…
|
…
|
… | |
|
144
|
233
|
1.618055556… | |
|
233
|
377
|
1.618025751… | |
|
…
|
…
|
… |

Então, assim como nós naturalmente temos sete braços quando usamos 0.142857 (1/7), tendemos a obter Números Fibonacci quando usamos a Golden Ratio.
Try contando os braços em espiral – as espirais de “viragem à esquerda”, e depois as espirais de “viragem à direita” … que números obtiveram?
Espiral Leaf Growth

Este comportamento interessante não se encontra apenas nas sementes de girassol.
As folhas, ramos e pétalas também podem crescer em espiral.
Porquê? Para que novas folhas não bloqueiem o sol de folhas mais velhas, ou para que a quantidade máxima de chuva ou orvalho seja direcionada para as raízes.
Na verdade, quando uma planta tem espirais a rotação tende a ser uma fração feita com dois Números Fibonacci sucessivos (um após o outro), por exemplo:
- Uma meia rotação é 1/2 (1 e 2 são Números Fibonacci)
- 3/5 também é comum (ambos Números Fibonacci), e
- 5/8 também (você adivinhou!)
todos se aproximam cada vez mais da Razão de Ouro.
|
E é por isso que os Números Fibonacci são muito comuns em plantas. Aqui é uma margarida com 21 pétalas |
 |
Mas não vemos isto em todas as plantas, pois a natureza tem muitos métodos diferentes de sobrevivência.
Ângulo de ouro
Até agora temos falado de “rotações” (rotações completas).
O equivalente a 0,61803… rotações é de 222,4922… graus, ou cerca de 222,5°.
Na outra direção é cerca de 137,5°, chamado “Golden Angle”.
Então, da próxima vez que você estiver andando no jardim, procure pelo Golden Angle,
e conte pétalas e folhas para encontrar o número de Fibonacci,
e descubra como as plantas são inteligentes… !
Exercício
Porque não vai ao jardim ou estaciona agora mesmo, e começa a contar folhas e pétalas, e a medir as rotações para ver o que encontra.
Pode escrever os seus resultados neste formulário:
| Nome ou Descrição da Planta: | ||||
| As Folhas Crescem em Espirais? S / N | ||||
| Conta um grupo de Folhas: | ||||
| > Quantas folhas (a) ? | ||||
| Quantas rotações completas (b) ? | ||||
| Rotação por folha (b/a) : | ||||
| Ângulo de rotação (360 × b/a) : | ||||
| Existem Flores? S / N | ||||
| Quantas pétalas na Flor 1: | ||||
| Flower 2: | ||||
| Flower 3: | ||||
(Mas lembre-se, a natureza tem as suas próprias regras, e não tem de seguir padrões matemáticos,
mas quando o faz é fantástico de se ver.)
* Notas sobre a animação
Sementes de girassol crescem do centro para fora, mas na animação eu achei mais fácil desenhar as sementes mais novas primeiro e adicionar as mais velhas.
A animação deve continuar por mais tempo para ser a mesma do girassol – isso resultaria em 55 espirais no sentido horário e 34 espirais no sentido anti-horário (números sucessivos de Fibonacci). Eu só não queria que demorasse muito.
As espirais não são programadas nela – elas ocorrem naturalmente como resultado de tentar colocar as sementes o mais próximo possível umas das outras, mantendo-as na rotação correta.

