Selection Sort – Algorithm, Source Code, Time Complexity

Ten artykuł jest częścią serii „Sorting Algorithms: Ultimate Guide” i…

• opisuje, jak działa Selection Sort,
• zawiera kod źródłowy Java dla Selection Sort,
• pokazuje, jak wyprowadzić jego złożoność czasową (bez skomplikowanej matematyki)
• i sprawdza, czy wydajność implementacji w Javie odpowiada oczekiwanemu zachowaniu w czasie wykonywania.

Kod źródłowy dla całej serii artykułów można znaleźć w moim repozytorium GitHub.

Przykład: Sortowanie kart do gry

Sortowanie kart do gry do ręki jest klasycznym przykładem dla Insertion Sort.

Selection Sort może być również zilustrowany za pomocą kart do gry. Nie znam nikogo, kto zbierałby swoje karty w ten sposób, ale jako przykład, działa to całkiem nieźle 😉

Najpierw kładziesz wszystkie swoje karty zakryte na stole przed sobą. Wyszukujesz najmniejszą kartę i bierzesz ją do lewej ręki. Następnie szukasz następnej większej karty i kładziesz ją na prawo od najmniejszej karty, i tak dalej, aż w końcu bierzesz największą kartę na prawo.

Różnica w stosunku do sortowania przez wkładanie

W sortowaniu przez wkładanie, braliśmy następną nieposortowaną kartę i wkładaliśmy ją na właściwą pozycję w posortowanych kartach.

Sortowanie przez wybieranie działa na odwrót: Z nieposortowanych kart wybieramy najmniejszą kartę, a następnie – jedna po drugiej – dołączamy ją do już posortowanych kart.

Algorytm Sortowania Selekcyjnego

Algorytm najprościej można wyjaśnić na przykładzie. W kolejnych krokach pokazuję, jak posortować tablicę za pomocą Sortowania Selekcyjnego:

Krok 1

Podzielimy tablicę na lewą, posortowaną część i prawą, nieposortowaną część. Część posortowana jest na początku pusta:

Krok 2

Szukamy najmniejszego elementu w prawej, nieposortowanej części. W tym celu najpierw zapamiętujemy pierwszy element, którym jest 6. Przechodzimy do następnego pola, gdzie znajdujemy jeszcze mniejszy element 2. Przechodzimy przez resztę tablicy, szukając jeszcze mniejszego elementu. Ponieważ nie możemy go znaleźć, zostajemy przy 2. Umieszczamy go na właściwej pozycji, zamieniając go z elementem na pierwszym miejscu. Następnie przesuwamy granicę między fragmentami tablicy o jedno pole w prawo:

Krok 3

Wyszukujemy ponownie w prawej, nieposortowanej części najmniejszy element. Tym razem jest to 3; zamieniamy go z elementem na drugiej pozycji:

Krok 4

Ponownie szukamy najmniejszego elementu w prawej części. Jest to 4, która już znajduje się we właściwej pozycji. Nie ma więc potrzeby wykonywania operacji zamiany w tym kroku, a jedynie przesuwamy granicę sekcji:

Krok 5

Jako najmniejszy element znajdujemy 6. Zamieniamy ją z elementem znajdującym się na początku prawej części, czyli 9:

Krok 6

Z pozostałych dwóch elementów najmniejszym jest 7. Zamieniamy go z 9:

Algorytm zakończony

Ostatni element jest automatycznie największy, a więc znajduje się na właściwej pozycji. Algorytm jest zakończony, a elementy są posortowane:

Kod źródłowy Java Selection Sort

W tym rozdziale znajdziesz prostą implementację Java Selection Sort.

Pętla zewnętrzna iteruje po elementach do posortowania i kończy się po drugim ostatnim elemencie. Gdy ten element zostanie posortowany, ostatni element również zostanie automatycznie posortowany. Zmienna pętli i zawsze wskazuje na pierwszy element prawej, nieposortowanej części.

W każdym cyklu pętli pierwszy element prawej części jest początkowo przyjmowany jako najmniejszy element min; jego pozycja jest przechowywana w minPos.

Pętla wewnętrzna iteruje następnie od drugiego elementu prawej części do jej końca i ponownie przypisuje min i minPos za każdym razem, gdy zostanie znaleziony jeszcze mniejszy element.

Po zakończeniu pętli wewnętrznej elementy o pozycjach i (początek prawej części) i minPos są zamieniane (chyba że są tym samym elementem).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

Przedstawiony kod różni się od klasy SelectionSort w repozytorium GitHub tym, że implementuje interfejs SortAlgorithm, aby można go było łatwo wymieniać w ramach frameworka testowego.

Złożoność czasowa sortowania selekcyjnego

Zaznaczamy przez n liczbę elementów, w naszym przykładzie n = 6.

Dwie zagnieżdżone pętle są wskazówką, że mamy do czynienia ze złożonością czasową* rzędu O(n²). Będzie tak, jeśli obie pętle iterują do wartości, która rośnie liniowo z n.

Tak jest oczywiście w przypadku pętli zewnętrznej: liczy ona do n-1.

A co z pętlą wewnętrzną?

Spójrz na poniższą ilustrację:

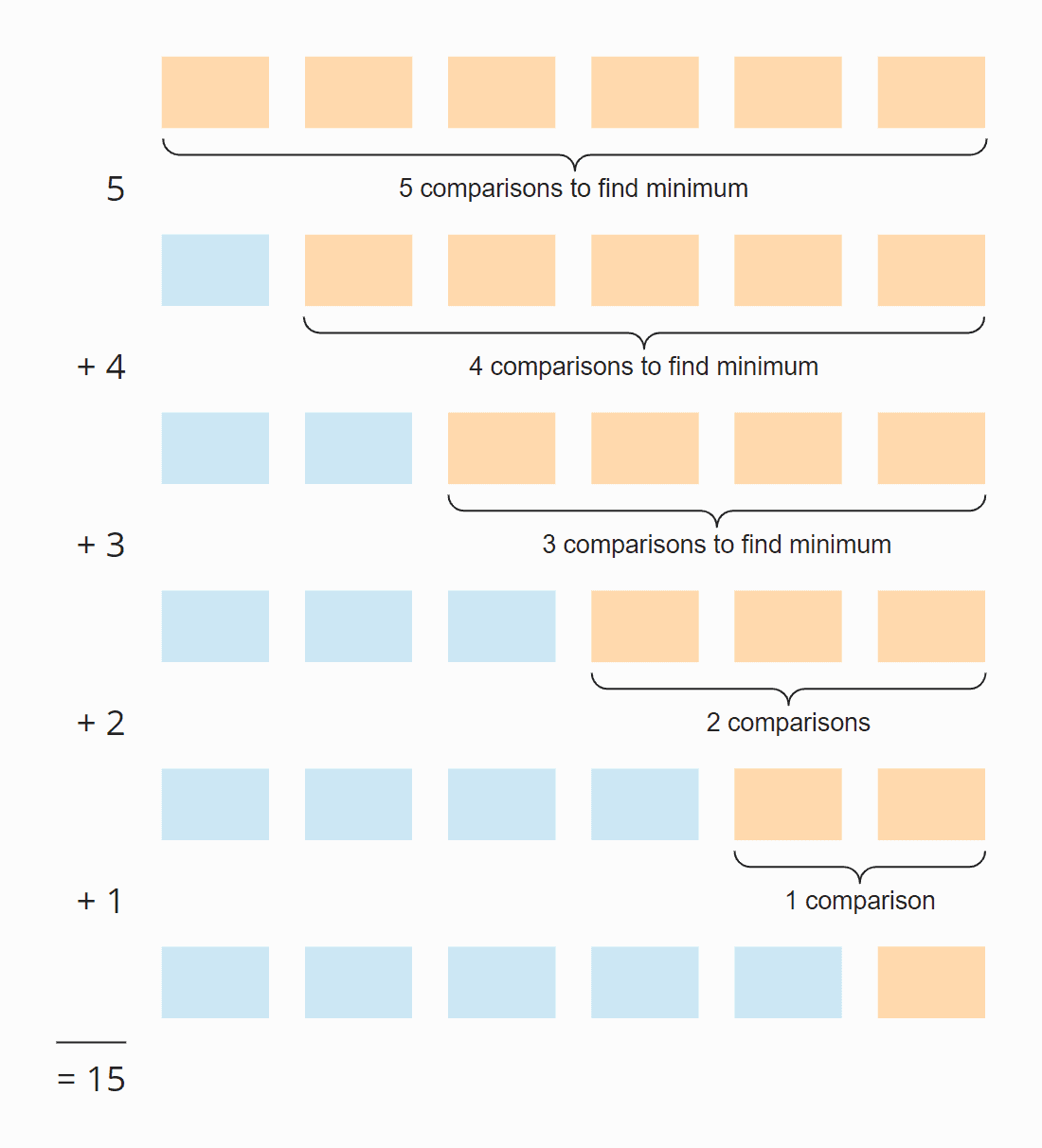
W każdym kroku liczba porównań jest o jeden mniejsza od liczby nieposortowanych elementów. W sumie jest 15 porównań – niezależnie od tego, czy tablica jest wstępnie posortowana, czy nie.

Można to również obliczyć w następujący sposób:

Sześć elementów razy pięć kroków; podzielone przez dwa, ponieważ średnio we wszystkich krokach połowa elementów jest nadal nieposortowana:

6 × 5 × ½ = 30 × ½ = 15

Jeśli zastąpimy 6 przez n, otrzymamy

n × (n – 1) × ½

Po pomnożeniu jest to:

½ n² – ½ n

Największą potęgą n w tym określeniu jest n². Złożoność czasowa wyszukiwania najmniejszego elementu wynosi zatem O(n²) – nazywana jest również „czasem kwadratowym”.

Przyjrzyjmy się teraz zamianie elementów. W każdym kroku (z wyjątkiem ostatniego), albo jeden element jest zamieniany, albo żaden, w zależności od tego, czy najmniejszy element jest już na właściwej pozycji, czy nie. Mamy więc w sumie maksymalnie n-1 operacji zamiany, czyli złożoność czasową O(n) – zwaną też „czasem liniowym”.

Dla całkowitej złożoności liczy się tylko najwyższa klasa złożoności, dlatego:

Średnia, best-case i worst-case złożoność czasowa Selection Sort to: O(n²)

* Pojęcia „złożoność czasowa” i „O-notacja” są wyjaśnione w tym artykule za pomocą przykładów i diagramów.

Runtime of the Java Selection Sort Example

Dość teorii! Napisałem program testowy, który mierzy czas działania Selection Sort (i wszystkich innych algorytmów sortowania omówionych w tej serii) w następujący sposób:

• Liczba elementów do posortowania podwaja się po każdej iteracji z początkowo 1 024 elementów do 536 870 912 (= 229) elementów. Tablica o dwukrotnie większym rozmiarze nie może być utworzona w Javie.
• Jeśli test trwa dłużej niż 20 sekund, tablica nie jest dalej rozszerzana.
• Wszystkie testy są przeprowadzane z elementami nieposortowanymi oraz wstępnie posortowanymi rosnąco i malejąco.
• Pozwalamy kompilatorowi HotSpot zoptymalizować kod za pomocą dwóch rund rozgrzewki. Następnie testy są powtarzane aż do przerwania procesu.

Po każdej iteracji program wypisuje medianę wszystkich poprzednich wyników pomiarów.

Oto wynik dla sortowania selekcyjnego po 50 iteracjach (dla jasności jest to tylko fragment; kompletny wynik można znaleźć tutaj):

n	nieposortowane	wstępujące	zstępujące
…	…	…	…
16,384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Tutaj pomiary jeszcze raz w formie wykresu (przy czym „niesortowane” i „rosnące” przedstawiłem jako jedną krzywą ze względu na prawie identyczne wartości):

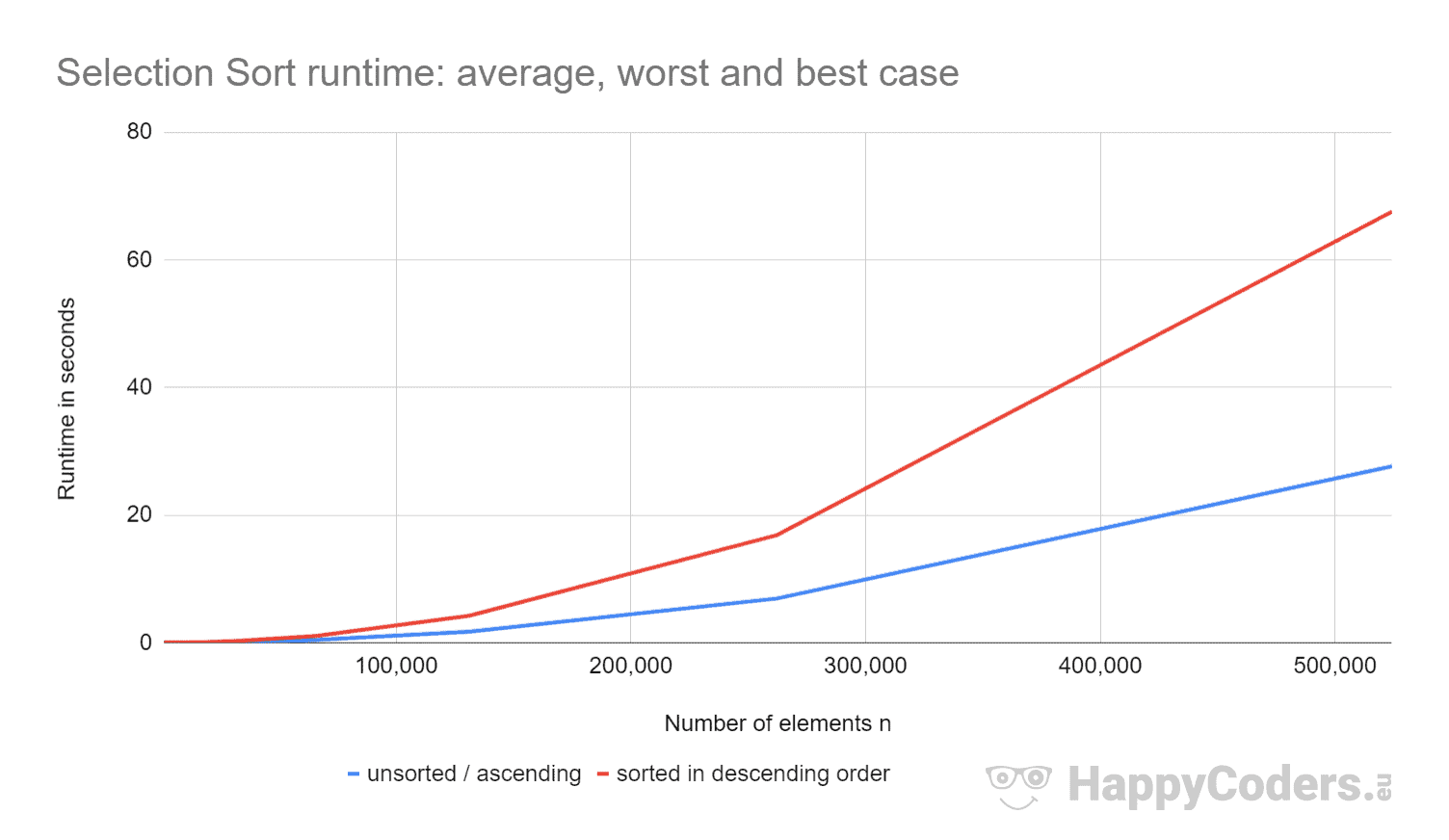
Dobrze jest zobaczyć, że

• jeśli liczba elementów jest podwojona, czas działania jest w przybliżeniu czterokrotnie zwiększony – niezależnie od tego, czy elementy są wcześniej posortowane, czy nie. Odpowiada to oczekiwanej złożoności czasowej O(n²).
• że czas działania dla elementów posortowanych rosnąco jest nieco lepszy niż dla elementów nieposortowanych. Wynika to z faktu, że operacje zamiany, które – jak wynika z powyższej analizy – mają niewielkie znaczenie, nie są tu konieczne.
• że czas działania dla elementów posortowanych malejąco jest znacznie gorszy niż dla elementów nieposortowanych.

Dlaczego tak jest?

Analiza czasu działania w najgorszym przypadku

Teoretycznie poszukiwanie najmniejszego elementu powinno zawsze zajmować tyle samo czasu, niezależnie od sytuacji początkowej. A operacji zamiany powinno być tylko nieco więcej dla elementów posortowanych malejąco (dla elementów posortowanych malejąco każdy element musiałby zostać zamieniony; dla elementów nieposortowanych prawie każdy element musiałby zostać zamieniony).

Używając programu CountOperations z mojego repozytorium GitHub, możemy zobaczyć liczbę różnych operacji. Oto wyniki dla nieposortowanych elementów i elementów posortowanych w porządku malejącym, podsumowanych w jednej tabeli:

.

n	Porównania	Swaps unsorted	Swaps descending	minPos/min unsorted	minPos/min descending
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

Z zmierzonych wartości można wywnioskować, że:

• Przy elementach posortowanych malejąco mamy – zgodnie z oczekiwaniami – tyle samo operacji porównania, co przy elementach nieposortowanych, czyli n × (n-1) / 2.
• Z nieposortowanymi elementami, mamy – zgodnie z założeniami – prawie tyle samo operacji zamiany co elementów: na przykład z 4096 nieposortowanymi elementami, jest 4084 operacji zamiany. Liczby te zmieniają się losowo z testu na test.
• Jednakże, z elementami posortowanymi w porządku malejącym, mamy tylko o połowę mniej operacji zamiany niż elementów! Dzieje się tak, ponieważ podczas zamiany nie tylko umieszczamy najmniejszy element na właściwym miejscu, ale także odpowiedniego partnera do zamiany.

Na przykład przy ośmiu elementach mamy cztery operacje zamiany. W pierwszych czterech iteracjach mamy po jednej, a w iteracjach od piątej do ósmej – żadnej (mimo to algorytm działa do końca):

Ponadto z pomiarów możemy odczytać:

• Przyczynę, dla której Selection Sort jest tak dużo wolniejszy przy elementach posortowanych malejąco, można znaleźć w liczbie przypisań zmiennych lokalnych (minPos i min) podczas poszukiwania najmniejszego elementu. Podczas gdy przy 8 192 nieposortowanych elementach mamy 69 378 takich przypisań, to przy elementach posortowanych malejąco jest ich 16 785 407 – czyli 242 razy więcej!

Skąd ta ogromna różnica?

Analiza czasu wykonania wyszukiwania najmniejszego elementu

Dla elementów posortowanych malejąco, rząd wielkości można wyprowadzić z powyższej ilustracji. Poszukiwanie najmniejszego elementu jest ograniczone do trójkąta pomarańczowych i pomarańczowo-niebieskich pól. W górnej pomarańczowej części, liczby w każdym polu stają się mniejsze; w prawej pomarańczowo-niebieskiej części, liczby ponownie wzrastają.

Operacje przypisania mają miejsce w każdym pomarańczowym polu i w pierwszym z pomarańczowo-niebieskich pól. Liczba operacji przypisania dla minPos i min wynosi więc, mówiąc obrazowo, około „ćwiartki kwadratu” – matematycznie i precyzyjnie jest to ¼ n² + n – 1.

W przypadku elementów nieposortowanych musielibyśmy wniknąć w sprawę znacznie głębiej. To nie tylko wykraczałoby poza zakres tego artykułu, ale całego bloga.

Dlatego ograniczam moją analizę do małego programu demonstracyjnego, który mierzy, ile przypisań minPos/min jest podczas wyszukiwania najmniejszego elementu w nieposortowanej tablicy. Oto średnie wartości po 100 iteracjach (mały wycinek; pełne wyniki można znaleźć tutaj):

n	średnia liczba zadań minPos/min
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Tutaj jako wykres z logarytmiczną osią x:

Wykres bardzo ładnie pokazuje, że mamy logarytmiczny wzrost, tzn, z każdym podwojeniem liczby elementów, liczba przypisań wzrasta tylko o stałą wartość. Jak już powiedziałem, nie będę zagłębiał się w matematyczne tło.

To jest powód, dla którego te minPos/min przypisania mają niewielkie znaczenie w nieposortowanych tablicach.

Inne cechy sortowania selekcyjnego

W kolejnych rozdziałach omówię złożoność przestrzenną, stabilność i równoległość sortowania selekcyjnego.

Złożoność przestrzenna sortowania selekcyjnego

Złożoność przestrzenna sortowania selekcyjnego jest stała, ponieważ nie potrzebujemy żadnego dodatkowego miejsca w pamięci poza zmiennymi pętli i i j oraz zmiennymi pomocniczymi length, minPos i min.

To znaczy, że bez względu na to, ile elementów sortujemy – dziesięć czy dziesięć milionów – zawsze potrzebujemy tylko tych pięciu dodatkowych zmiennych. Stały czas notujemy jako O(1).

Stabilność sortowania selekcyjnego

Sortowanie selekcyjne wydaje się stabilne na pierwszy rzut oka: Jeśli część nieposortowana zawiera kilka elementów z tym samym kluczem, to pierwszy z nich powinien być dołączony do części posortowanej jako pierwszy.

Ale pozory mylą. Ponieważ zamieniając dwa elementy w drugim podkroku algorytmu, może się zdarzyć, że pewne elementy w części nieposortowanej nie będą już miały oryginalnej kolejności. To z kolei prowadzi do tego, że nie występują one już w oryginalnej kolejności w części posortowanej.

Przykład można skonstruować bardzo prosto. Załóżmy, że mamy dwa różne elementy z kluczem 2 i jeden z kluczem 1, ułożone w następujący sposób, a następnie sortujemy je za pomocą Selection Sort:

W pierwszym kroku pierwszy i ostatni element są zamieniane. W ten sposób element „TWO” znajduje się za elementem „two” – kolejność obu elementów jest zamieniana.

W drugim kroku algorytm porównuje dwa tylne elementy. Oba mają ten sam klucz, 2. Żaden element nie jest więc zamieniany.

W trzecim kroku pozostaje tylko jeden element; jest on automatycznie uznawany za posortowany.

Dwa elementy z kluczem 2 zostały więc zamienione na swoją początkową kolejność – algorytm jest niestabilny.

Stable Variant of Selection Sort

Selection Sort można uczynić stabilnym, nie zamieniając najmniejszego elementu z pierwszym w kroku drugim, lecz przesuwając wszystkie elementy między pierwszym a najmniejszym elementem o jedną pozycję w prawo i wstawiając najmniejszy element na początek.

Mimo że złożoność czasowa pozostanie taka sama dzięki tej zmianie, dodatkowe przesunięcia doprowadzą do znacznego spadku wydajności, przynajmniej gdy sortujemy tablicę.

W przypadku listy połączonej wycinanie i wklejanie elementu, który ma być posortowany, można by wykonać bez znaczącego spadku wydajności.

Paralelizowalność sortowania selekcyjnego

Nie możemy paralelizować zewnętrznej pętli, ponieważ zmienia ona zawartość tablicy w każdej iteracji.

Pętlę wewnętrzną (szukanie najmniejszego elementu) można sparalelizować, dzieląc tablicę, szukając równolegle najmniejszego elementu w każdej podtablicy i łącząc pośrednie wyniki.

Selection Sort vs. Insertion Sort

Który algorytm jest szybszy, Selection Sort, czy Insertion Sort?

Porównajmy pomiary z moich implementacji w Javie.

Opuszczam najlepszy przypadek. W przypadku Insertion Sort, złożoność czasowa najlepszego przypadku to O(n) i zajęła mniej niż milisekundę dla maksymalnie 524 288 elementów. Tak więc w najlepszym przypadku, Insertion Sort jest, dla dowolnej liczby elementów, rzędy wielkości szybszy niż Selection Sort.

n	Selection Sort unsorted	Insertion Sort unsorted	Selection Sort descending	Insertion Sort descending
…	…	…	…	…
16,384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65,536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46.309,3 ms

I jeszcze raz jako diagram:

Insertion Sort jest zatem nie tylko szybszy od Selection Sort w najlepszym przypadku, ale także w średnim i najgorszym przypadku.

Powodem tego jest fakt, że Insertion Sort wymaga średnio o połowę mniej porównań. Dla przypomnienia, w przypadku Insertion Sort mamy porównania i przesunięcia uśredniające do połowy posortowanych elementów; w przypadku Selection Sort musimy w każdym kroku szukać najmniejszego elementu we wszystkich nieposortowanych elementach.

Selection Sort ma znacznie mniej operacji zapisu, więc Selection Sort może być szybszy, gdy operacje zapisu są drogie. Nie ma to miejsca w przypadku sekwencyjnych zapisów do tablic, ponieważ są one wykonywane głównie w pamięci podręcznej procesora.

W praktyce Selection Sort jest więc prawie nigdy nieużywany.

Podsumowanie

Selection Sort jest łatwym w implementacji, a w typowej implementacji niestabilnym, algorytmem sortującym o średniej, najlepszej i najgorszej złożoności czasowej O(n²).

Selection Sort jest wolniejszy niż Insertion Sort, dlatego jest rzadko używany w praktyce.

Więcej algorytmów sortowania znajdziesz w tym przeglądzie wszystkich algorytmów sortowania i ich charakterystyce w pierwszej części serii artykułów.

Jeśli podobał Ci się artykuł, nie krępuj się udostępnić go za pomocą jednego z przycisków udostępniania na końcu. Czy chcesz być informowany przez e-mail, gdy opublikuję nowy artykuł? W takim razie skorzystaj z poniższego formularza, aby zapisać się do mojego newslettera.

.