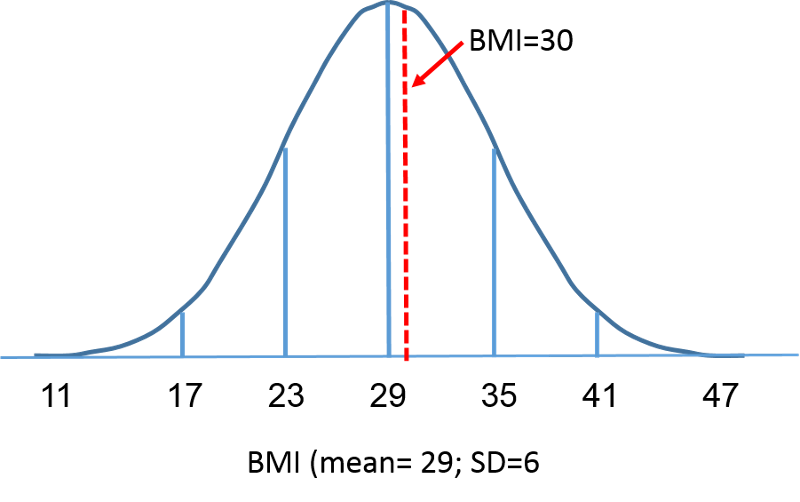
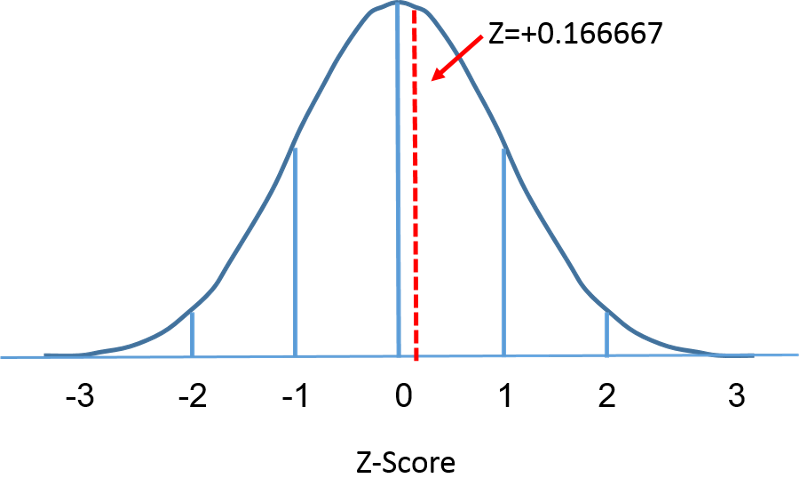
Standardowy rozkład normalny jest rozkładem normalnym o średniej równej zero i odchyleniu standardowym równym 1. Standardowy rozkład normalny jest wyśrodkowany w punkcie zero, a stopień, w jakim dany pomiar odbiega od średniej, jest określony przez odchylenie standardowe. Dla standardowego rozkładu normalnego 68% obserwacji leży w granicach 1 odchylenia standardowego od średniej, 95% leży w granicach dwóch odchyleń standardowych od średniej, a 99,9% leży w granicach 3 odchyleń standardowych od średniej. Do tej pory używaliśmy „X” do oznaczenia interesującej nas zmiennej (np. X=BMI, X=wysokość, X=waga). Jednak w przypadku standardowego rozkładu normalnego, będziemy używać „Z”, aby odnieść się do zmiennej w kontekście standardowego rozkładu normalnego. Po standaryzacji, BMI=30 omawiane na poprzedniej stronie jest pokazane poniżej leżąc 0.16667 jednostek powyżej średniej 0 na standardowym rozkładzie normalnym po prawej stronie.
 ====
====
Ponieważ obszar pod krzywą standardową = 1, możemy zacząć bardziej precyzyjnie określać prawdopodobieństwa konkretnych obserwacji. Dla każdego danego wyniku Z możemy obliczyć obszar pod krzywą na lewo od tego wyniku Z. Tabela w ramce poniżej pokazuje prawdopodobieństwa dla standardowego rozkładu normalnego. Przyjrzyj się tabeli i zauważ, że wynik „Z” równy 0.0 pokazuje prawdopodobieństwo 0.50 lub 50%, a wynik „Z” równy 1, czyli jedno odchylenie standardowe powyżej średniej, pokazuje prawdopodobieństwo 0.8413 lub 84%. To dlatego, że jedno odchylenie standardowe powyżej i poniżej średniej obejmuje około 68% obszaru, więc jedno odchylenie standardowe powyżej średniej reprezentuje połowę z tego 34%. Tak więc, 50% poniżej średniej plus 34% powyżej średniej daje nam 84%.
Prawdopodobieństwo standardowego rozkładu normalnego Z
![]()
Ta tabela jest zorganizowana w celu zapewnienia obszaru pod krzywą na lewo od lub mniej od określonej wartości lub „wartości Z”. W tym przypadku, ponieważ średnia wynosi zero, a odchylenie standardowe 1, wartość Z jest liczbą jednostek odchylenia standardowego z dala od średniej, a obszar jest prawdopodobieństwem zaobserwowania wartości mniejszej niż ta konkretna wartość Z. Zauważmy również, że tabela pokazuje prawdopodobieństwa do dwóch miejsc po przecinku Z. Miejsce jednostek i pierwsze miejsce po przecinku są pokazane w lewej kolumnie, a drugie miejsce po przecinku jest wyświetlane w górnym rzędzie.
Wróćmy jednak do pytania o prawdopodobieństwo, że BMI jest mniejsze niż 30, czyli P(X<30). Na to pytanie możemy odpowiedzieć posługując się standardowym rozkładem normalnym. Na poniższych rysunkach przedstawiono obok siebie rozkłady BMI dla mężczyzn w wieku 60 lat oraz standardowy rozkład normalny.
Rozkład BMI i standardowy rozkład normalny
 ====
====
Powierzchnia pod każdą krzywą jest taka sama, ale skalowanie osi X jest inne. Zauważ jednak, że obszary na lewo od linii przerywanej są takie same. Rozkład BMI zawiera się w przedziale od 11 do 47, podczas gdy standaryzowany rozkład normalny, Z, zawiera się w przedziale od -3 do 3. Chcemy obliczyć P(X < 30). Aby to zrobić, możemy określić wartość Z, która odpowiada X = 30, a następnie użyć powyższej tabeli standardowego rozkładu normalnego, aby znaleźć prawdopodobieństwo lub obszar pod krzywą. Poniższy wzór przekształca wartość X w wynik Z, zwany również wynikiem standaryzowanym:

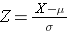
gdzie μ jest średnią, a σ jest odchyleniem standardowym zmiennej X.
Aby obliczyć P(X < 30) zamieniamy X=30 na odpowiadający mu wynik Z (nazywamy to standaryzacją):

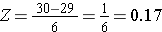
Tak więc, P(X < 30) = P(Z < 0.17). Możemy następnie sprawdzić odpowiednie prawdopodobieństwo dla tego wyniku Z ze standardowej tabeli rozkładu normalnego, która pokazuje, że P(X < 30) = P(Z < 0.17) = 0.5675. Zatem prawdopodobieństwo, że mężczyzna w wieku 60 lat ma BMI mniejsze niż 30 wynosi 56,75%.
Inny przykład
Używając tego samego rozkładu dla BMI, jakie jest prawdopodobieństwo, że mężczyzna w wieku 60 lat ma BMI przekraczające 35? Innymi słowy, ile wynosi P(X > 35)? Ponownie dokonujemy standaryzacji:

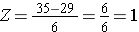
Teraz przechodzimy do tabeli standardowego rozkładu normalnego, aby sprawdzić P(Z>1) i dla Z=1,00 znajdujemy, że P(Z<1,00) = 0,8413. Zauważmy jednak, że tabela zawsze podaje prawdopodobieństwo, że Z jest mniejsze od podanej wartości, czyli daje nam P(Z<1)=0,8413.
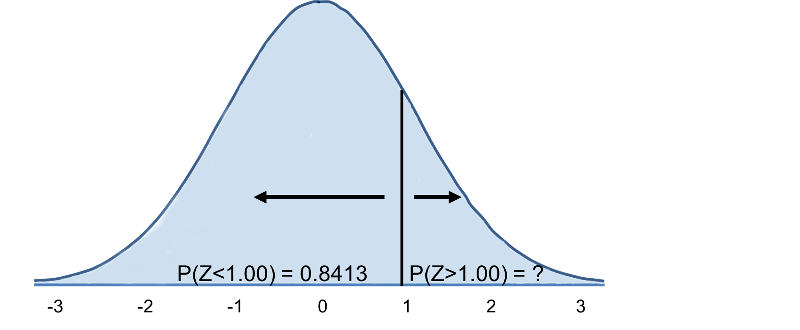
Stąd P(Z>1)=1-0,8413=0,1587. Interpretacja: Prawie 16% mężczyzn w wieku 60 lat ma BMI powyżej 35.
Kalkulator prawdopodobieństwa normalnego
![]()
![]()
Z-Scores with R
As alternative to looking up normal probabilities in the table or using Excel, we can use R to compute probabilities. Na przykład,
> pnorm(0)
Score Z równy 0 (średnia dowolnego rozkładu) ma 50% obszaru po lewej stronie. Jakie jest prawdopodobieństwo, że 60-letni mężczyzna z powyższej populacji ma BMI mniejsze niż 29 (średnia)? Z-score wynosiłby 0, a pnorm(0)=0,5 lub 50%.
Jakie jest prawdopodobieństwo, że 60-letni mężczyzna będzie miał BMI mniejsze niż 30? Wartość Z-score wyniosła 0,16667.
> pnorm(0,16667)
Więc prawdopodobieństwo wynosi 56,6%.
Jakie jest prawdopodobieństwo, że 60-letni mężczyzna będzie miał BMI większe niż 35?
35-29=6, czyli jedno odchylenie standardowe powyżej średniej. Możemy więc obliczyć obszar po lewej stronie
> pnorm(1)
, a następnie odjąć wynik od 1,0.
1-0,8413447= 0,1586553
Więc prawdopodobieństwo, że 60-letni mężczyzna będzie miał BMI większe niż 35 wynosi 15,8%.
Albo, możemy użyć R do obliczenia tego wszystkiego w jednym kroku, jak poniżej:
> 1-pnorm(1)
Probability for a Range of Values

Jakie jest prawdopodobieństwo, że mężczyzna w wieku 60 lat ma BMI pomiędzy 30 a 35? Zauważmy, że jest to to samo pytanie co pytanie o to, jaka część mężczyzn w wieku 60 lat ma BMI między 30 a 35. Konkretnie, chcemy P(30 < X < 35)? Wcześniej obliczyliśmy P(30<X) i P(X<35); jak można wykorzystać te dwa wyniki do obliczenia prawdopodobieństwa, że BMI będzie pomiędzy 30 a 35? Spróbuj sformułować i odpowiedzieć samodzielnie przed zapoznaniem się z poniższym wyjaśnieniem.
Odpowiedź