Równanie w postaci punktu przecięcia zbocza jest zapisywane jako
$y=mx+b$$
Gdzie m jest nachyleniem linii, a b jest punktem przecięcia y. Możesz użyć tego równania, aby napisać równanie, jeśli znasz nachylenie i punkt przecięcia y.
Przykład
Znajdź równanie prostej
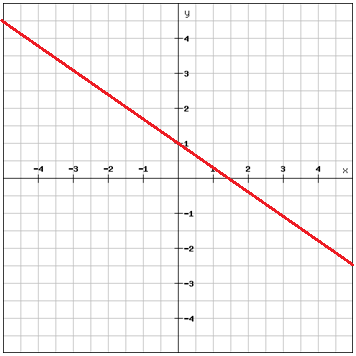
Wybierz dwa punkty, które leżą na prostej
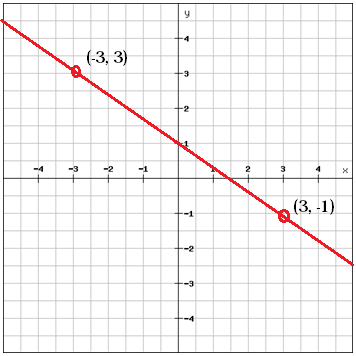
Oblicz nachylenie między tymi dwoma punktami
$m=frac{y_{2}}, -y_{1}}{x_{2}}, -x_{1}}=}frac{lewa (-1 prawo )-3}{3-lewa ( -3 prawo )}=frac{-4}{6}=frac{-2}{3}$$
Możemy znaleźć wartość b, punkt przecięcia y, patrząc na wykres
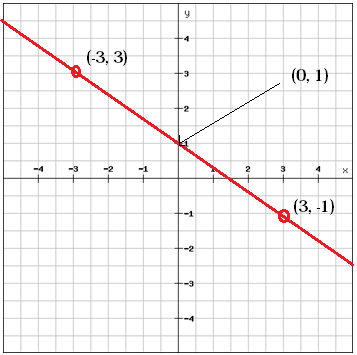
b = 1
Mamy wartość dla m i wartość dla b. Daje nam to funkcję liniową
$$y=-frac{2}{3}x+1$$
W wielu przypadkach wartość b nie jest tak łatwa do odczytania. W takich przypadkach, lub jeśli nie jesteś pewien, czy prosta rzeczywiście przecina oś y w tym konkretnym punkcie, możesz obliczyć b rozwiązując równanie dla b, a następnie zastępując x i y jednym z twoich dwóch punktów.
Możemy użyć powyższego przykładu, aby to zilustrować. Mamy dwa punkty (-3, 3) i (3, -1). Na podstawie tych dwóch punktów obliczyliśmy nachylenie
$$m=- \frac{2}{3}$$
Daje nam to równanie
$$y=-.\frac{2}{3}x+b$$
Z tego możemy rozwiązać równanie dla b
$b=y+\frac{2}{3}x$$
I jeśli wstawimy wartości z naszego pierwszego punktu (-3, 3) otrzymamy
$b=3+frac{2}{3}x$$
$y=-.\frac{2}{3}x+1$$
co jest tym samym równaniem, które otrzymaliśmy, gdy odczytaliśmy punkt przecięcia y z wykresu.
Podsumowując, jak napisać równanie liniowe za pomocą postaci nachylenie-przyczyna, można
- Zidentyfikować nachylenie, m. Można to zrobić, obliczając nachylenie między dwoma znanymi punktami prostej za pomocą wzoru na nachylenie.
- Znaleźć punkt przecięcia y. Można to zrobić, podstawiając nachylenie i współrzędne punktu (x, y) na prostej do wzoru na punkt przecięcia nachylenia, a następnie rozwiązać dla b.
Gdy już masz zarówno m, jak i b, możesz po prostu wstawić je do równania w odpowiednich miejscach.
Lekcja wideo
Znajdź równanie wykresu
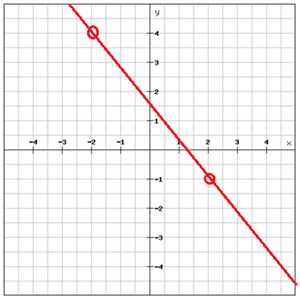
.