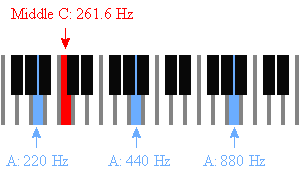
Jakie są częstotliwości nut muzycznych?

Nota
C
C#
D
D#
E
F
F#
G
G#
A
A#
B

Częstotliwość
261.63
277.18
293.66
311.13
329.63
349.23
369.99
392
415.3
440
466.16
493.88

Znajdują się one przy użyciu

częstotliwości `= 440×2^(n”/”12)`

dla `n = -21, -19, …., 27`

Skąd się wziął ten wzór?

Ten problem przypomniał mi o Odsetkach Złożonych, które poznaliśmy wcześniej w Matematyce Pieniężnej. Częstotliwość musi się podwajać co `12` nut (ponieważ w każdej oktawie jest `7` nut białych i `5` nut czarnych).

Tutaj jest wykres tej zależności:

częstotliwość `= 440×2^(n”/”12)`

To jest krzywa wykładnicza, którą poznaliśmy wcześniej w Wykresach funkcji wykładniczych.

Strojenie równomiernie temperowane

Ciekawy problem stoi przed twórcami instrumentów muzycznych od setek lat. Aby uzyskać „doskonałą piątkę” (interwał pomiędzy A i E powyżej, powiedzmy), musimy zagrać nutę, która ma `1.5` razy częstotliwość A.

Na skrzypcach (lub altówce lub jakimkolwiek innym instrumencie strunowym) jest to możliwe, i możemy zagrać piękne, doskonałe E na `440 × 1.5 = 660 „Hz”`. Ale zauważ (z tabeli częstotliwości powyżej), że fortepian grający tę samą nutę zagra E `= 659.26 „Hz”` .

Około 400 lat temu, klawiatury (zwykle klawesyny i organy) były strojone dla określonej grupy klawiszy, tak że wszystkie instrumenty, zwłaszcza struny, brzmiały „dobrze” w tych klawiszach. Klawesyn brzmiał świetnie w tych kluczach, ale dość okropnie w innych, niepowiązanych kluczach (powiedzmy B flat).

W rzeczywistości istniało kilka różnych systemów strojenia w użyciu w czasach Bacha, w tym meantone (który miał na celu sprawienie, by 3 tercje durowe brzmiały dobrze, ale nie był tak zaniepokojony jakością 5 tercji durowych, co skutkowało tym, że niektóre klawisze nie nadawały się do użytku), oraz strojenie Werckmeistera z 1691 roku, które pozwalało kompozytorom tworzyć muzykę w każdej tonacji (co skutkowało tym, że różne klawisze miały różną jakość tonalną).

Na początku XX wieku zdecydowano się na strojenie klawiatur w taki sposób, aby nuty były rozmieszczone równomiernie (jak częstotliwości podane w tabeli powyżej). Jest to tzw. strojenie równomiernie temperowane. Takie strojenie było znane w czasach Bacha, ale zostało odrzucone, ponieważ było uważane za zbyt „nijakie” (wszystkie klawisze mają tę samą jakość dźwięku) i nie było narzędzi do pomiaru częstotliwości, które pozwoliłyby na dokładne strojenie.

Niestety, strojenie równomiernie temperowane oznacza, że wszystkie instrumenty strunowe muszą pozwolić sobie na niewielkie różnice w strojeniu pomiędzy instrumentami, gdy klawiatury są również zaangażowane. Struny są zazwyczaj najszczęśliwsze, gdy grają tylko z innymi strunami, z tego powodu.