In de onderstaande frequentietabel staat A = 440 Hz, en dan
A# = 466,16 Hz,
B = 493,88 Hz,
C = 523,25 Hz, enz.
Ook vind je Midden-C: 261.63 Hz.
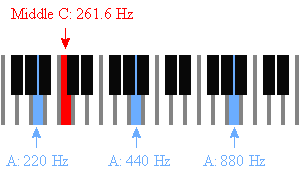
Tabel van muzikale frequenties
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
130.82
138.59
146.83
155.56
164.81
174.61
185
196
207.65
220
233.08
246.94
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
261.63
277.18
293.66
311.13
329.63
349.23
369.99
392
415.3
440
466.16
493.88
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
523.25
554.37
587.33
622.25
659.26
698.46
739.99
783.99
830.61
880
932.33
987.77
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
C
Frequentie
1046.5
1108.73
1174.66
1244.51
1318.51
1396.91
1479.98
1567.98
1661.22
1760
1864.66
1975.53
2093.00
Deze zijn gevonden met
frequentie `= 440×2^(n”/”12)`
voor `n = -21, -19, …., 27`
Waar komt deze formule vandaan?
Dit probleem deed me denken aan Samengestelde interest die we eerder in Geldrekenen hebben ontmoet. De frequentie moet elke `12` noten verdubbelen (omdat er `7` witte noten en `5` zwarte noten in elk octaaf zitten)
Hier is een grafiek van die relatie:
frequentie `= 440×2^(n”/”12)`
Dit is een exponentiële kromme, die we eerder hebben ontmoet in Graphs of Exponential Functions.
Gelijkzwevende stemming
Een interessant probleem stelt makers van muziekinstrumenten al honderden jaren voor. Om een “perfecte 5e” te krijgen (het interval tussen A en de E erboven, zeg), moeten we een toon spelen die `1.5` maal de frequentie van A heeft.
Op een viool (of altviool of een ander fretloos snaarinstrument) is dit mogelijk, en kunnen we een mooie, perfecte E spelen op `440 × 1.5 = 660 “Hz”`. Maar merk op (uit de frequentie tabel hierboven) dat een piano die dezelfde toon speelt E `= 659.26 “Hz”` speelt.
Rond 400 jaar geleden werden keyboards (meestal klavecimbels en orgels) gestemd voor een bepaalde groep toetsen, zodat alle instrumenten, vooral strijkers, “juist” klonken in die toetsen. Het klavecimbel klonk geweldig in die toonsoorten, maar afschuwelijk in andere niet verwante toonsoorten (bijvoorbeeld Bes).
Er waren eigenlijk verschillende stemmingen in gebruik in de tijd van Bach, waaronder de middentoonstemming (die tot doel had om grote tertsen goed te laten klinken, maar zich niet zo druk maakte over de kwaliteit van grote kwinten, met als gevolg dat sommige toonsoorten niet bruikbaar waren), en Werckmeister’s 1691 stemming, die componisten in staat stelde om muziek te maken in elke toonsoort (met als gevolg dat de verschillende toonsoorten een verschillende klankkwaliteit hadden).
In het begin van de 20e eeuw besloot men de klavieren zo te stemmen dat de tonen gelijkmatig verdeeld waren (zoals de frequenties in de bovenstaande tabel). Dit wordt gelijkzwevende stemming genoemd. Een dergelijke stemming was bekend in de tijd van Bach, maar werd verworpen omdat ze als te “flauw” werd beschouwd (alle toetsen hebben dezelfde toonkwaliteit) en er geen frequentiemeetinstrumenten waren die exacte stemmingen mogelijk zouden hebben gemaakt.
Helaas betekent gelijkzwevende stemming dat alle snaarinstrumenten rekening moeten houden met de kleine verschillen in stemmingen tussen instrumenten als er ook klavieren bij betrokken zijn. Snaren zijn meestal het gelukkigst wanneer ze alleen met andere snaren spelen, om deze reden.
top
Zoek IntMath
Online Trigonometrie Solver
Deze trigonometrie solver kan een breed scala van wiskunde problemen oplossen.
Ga naar: Online goniometrie solver