Selection Sort – Algoritme, broncode, tijdcomplexiteit

Dit artikel maakt deel uit van de serie “Sorteeralgoritmen: Ultimate Guide” en…

• beschrijft hoe Selection Sort werkt,
• omvat de Java-broncode voor Selection Sort,
• legt uit hoe de tijdcomplexiteit kan worden afgeleid (zonder ingewikkelde wiskunde)
• en controleert of de prestaties van de Java-implementatie overeenkomen met het verwachte runtime-gedrag.

U kunt de broncode voor de hele serie artikelen vinden in mijn GitHub repository.

Voorbeeld: Speelkaarten sorteren

Speelkaarten in de hand sorteren is het klassieke voorbeeld voor Insertion Sort.

Selection Sort kan ook geïllustreerd worden met speelkaarten. Ik ken niemand die zijn kaarten op deze manier oppakt, maar als voorbeeld werkt het best goed 😉

Eerst leg je al je kaarten open voor je op tafel. Je zoekt de kleinste kaart en neemt die naar de linkerkant van je hand. Dan zoek je de volgende grotere kaart en legt die rechts van de kleinste kaart, en zo verder tot je uiteindelijk de grootste kaart helemaal rechts pakt.

Verschil met Insertion Sort

Met Insertion Sort hebben we de volgende ongesorteerde kaart genomen en die op de juiste plaats in de gesorteerde kaarten gelegd.

Selection Sort werkt een beetje andersom: We selecteren de kleinste kaart uit de ongesorteerde kaarten en voegen die vervolgens – de een na de ander – toe aan de reeds gesorteerde kaarten.

Selection Sort Algoritme

Het algoritme kan het eenvoudigst worden uitgelegd aan de hand van een voorbeeld. In de volgende stappen laat ik zien hoe je de array sorteert met Selection Sort:

Stap 1

We verdelen de array in een linker, gesorteerd deel en een rechter, ongesorteerd deel. Het gesorteerde deel is aan het begin leeg:

Stap 2

We zoeken naar het kleinste element in het rechter, ongesorteerde deel. Daartoe onthouden we eerst het eerste element, dat is de 6. We gaan naar het volgende veld, waar we een nog kleiner element vinden in de 2. We lopen over de rest van de array, op zoek naar een nog kleiner element. Omdat we er geen vinden, houden we het bij de 2. We zetten het op de juiste plaats door het te verwisselen met het element op de eerste plaats. Dan verplaatsen we de grens tussen de array-gedeelten één veld naar rechts:

Stap 3

We zoeken opnieuw in het rechter, ongesorteerde deel naar het kleinste element. Deze keer is het de 3; we verwisselen het met het element op de tweede positie:

Stap 4

Opnieuw zoeken we naar het kleinste element in het rechter gedeelte. Het is de 4, die al op de juiste plaats staat. In deze stap is verwisselen dus niet nodig, en we verplaatsen gewoon de sectierand:

Stap 5

Als kleinste element vinden we de 6. We verwisselen het met het element aan het begin van het rechterdeel, de 9:

Stap 6

Van de resterende twee elementen is de 7 het kleinste. We verwisselen het met de 9:

Algoritme voltooid

Het laatste element is automatisch het grootste en staat dus op de juiste plaats. Het algoritme is voltooid, en de elementen zijn gesorteerd:

Selection Sort Java Source Code

In dit gedeelte vindt u een eenvoudige Java-implementatie van Selection Sort.

De buitenste lus itereert over de elementen die moeten worden gesorteerd, en deze eindigt na het op een na laatste element. Wanneer dit element is gesorteerd, wordt het laatste element automatisch ook gesorteerd. De lus-variabele i wijst altijd naar het eerste element van het rechter, ongesorteerde deel.

In elke lus-cyclus wordt het eerste element van het rechter deel initieel aangenomen als het kleinste element min; zijn positie wordt opgeslagen in minPos.

De binnenste lus loopt dan van het tweede element van het rechter gedeelte naar het einde en wijst min en minPos opnieuw toe wanneer een nog kleiner element wordt gevonden.

Nadat de binnenste lus is voltooid, worden de elementen van de posities i (begin van het rechter gedeelte) en minPos verwisseld (tenzij ze hetzelfde element zijn).

public class SelectionSort { public static void sort(int elements) { int length = elements.length; for (int i = 0; i < length - 1; i++) { // Search the smallest element in the remaining array int minPos = i; int min = elements; for (int j = i + 1; j < length; j++) { if (elements < min) { minPos = j; min = elements; } } // Swap min with element at pos i if (minPos != i) { elements = elements; elements = min; } } }}

De getoonde code verschilt van de SelectionSort klasse in de GitHub repository in die zin dat het de SortAlgorithm interface implementeert om gemakkelijk uitwisselbaar te zijn binnen het test framework.

Selection Sort Tijd Complexiteit

We duiden met n het aantal elementen aan, in ons voorbeeld n = 6.

De twee geneste lussen zijn een indicatie dat we te maken hebben met een tijd complexiteit* van O(n²). Dit zal het geval zijn als beide lussen itereren naar een waarde die lineair toeneemt met n.

Het is duidelijk het geval met de buitenste lus: deze telt op tot n-1.

Hoe zit het met de binnenste lus?

Kijk eens naar de volgende illustratie:

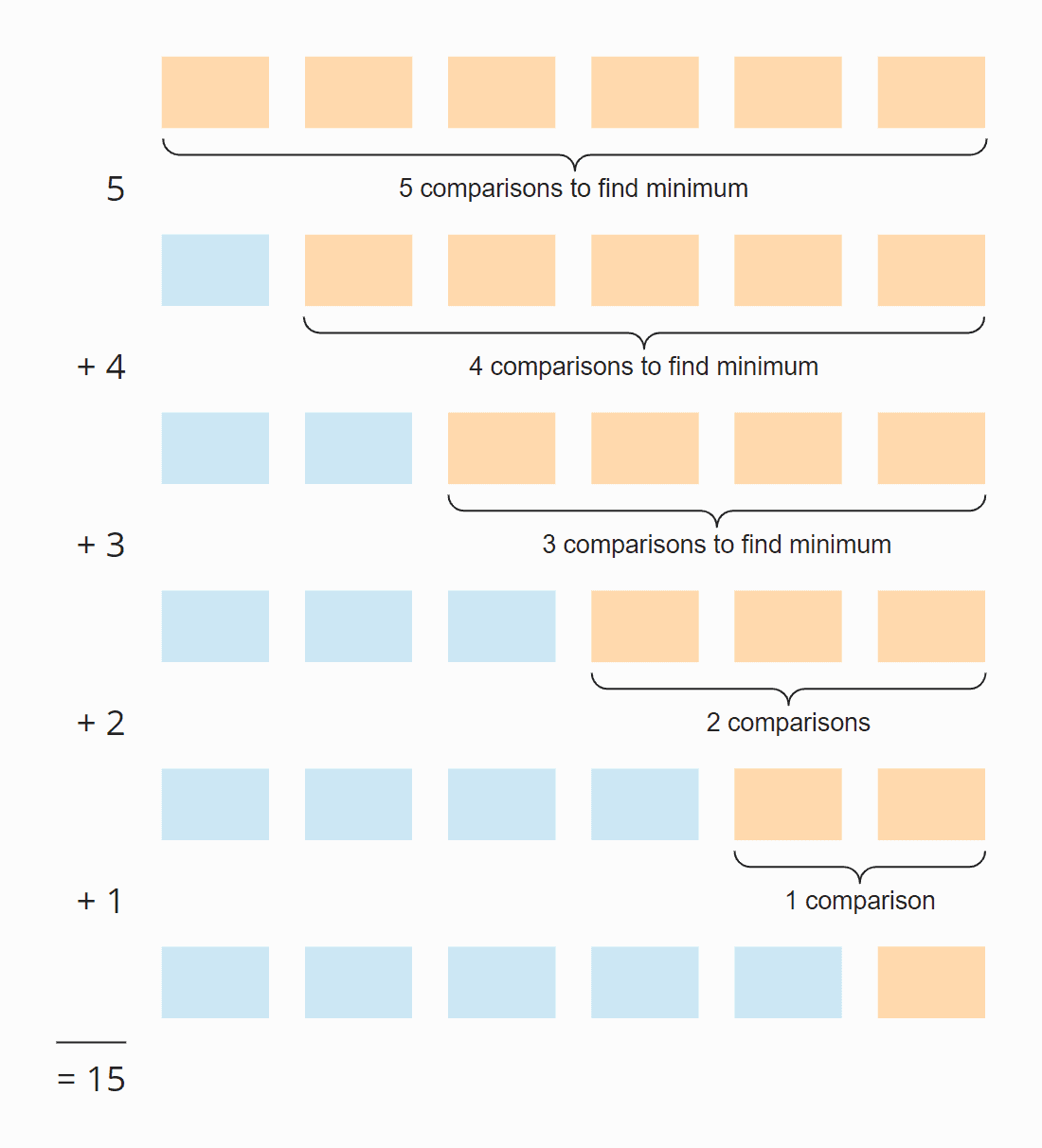
In elke stap is het aantal vergelijkingen één minder dan het aantal ongesorteerde elementen. In totaal zijn er 15 vergelijkingen – ongeacht of de matrix aanvankelijk gesorteerd is of niet.

Dit kan ook als volgt worden berekend:

Zes elementen maal vijf stappen; gedeeld door twee, want gemiddeld over alle stappen is de helft van de elementen nog ongesorteerd:

6 × 5 × ½ = 30 × ½ = 15

Vervangen we 6 door n, dan krijgen we

n × (n – 1) × ½

Vermenigvuldigd is dat:

½ n² – ½ n

De hoogste macht van n in deze term is n². De tijdcomplexiteit voor het zoeken van het kleinste element is dus O(n²) – ook wel “kwadratische tijd” genoemd.

Laten we nu eens kijken naar het verwisselen van de elementen. In elke stap (behalve de laatste) wordt één element verwisseld of geen enkel, afhankelijk van het feit of het kleinste element al op de juiste plaats staat of niet. In totaal hebben we dus maximaal n-1 verwisseloperaties, d.w.z. een tijdcomplexiteit van O(n) – ook wel “lineaire tijd” genoemd.

Voor de totale complexiteit is alleen de hoogste complexiteitsklasse van belang, dus:

De gemiddelde, best-case, en worst-case tijdcomplexiteit van Selection Sort is: O(n²)

* De termen “tijdcomplexiteit” en “O-notatie” worden in dit artikel uitgelegd aan de hand van voorbeelden en diagrammen.

Runtime van het Java Selection Sort Voorbeeld

Genoeg theorie! Ik heb een testprogramma geschreven dat de runtime van Selection Sort (en alle andere sorteeralgoritmen die in deze serie worden behandeld) als volgt meet:

• Het aantal te sorteren elementen verdubbelt na elke iteratie van aanvankelijk 1.024 elementen tot 536.870.912 (= 229) elementen. Een array van twee keer deze grootte kan in Java niet worden gemaakt.
• Als een test langer dan 20 seconden duurt, wordt de array niet verder uitgebreid.
• Alle tests worden uitgevoerd met zowel ongesorteerde als oplopende en aflopende voorgesorteerde elementen.
• We laten de HotSpot-compiler de code optimaliseren met twee opwarmrondes. Daarna worden de tests herhaald tot het proces wordt afgebroken.

Na elke iteratie drukt het programma de mediaan van alle vorige meetresultaten af.

Hier volgt het resultaat voor Selection Sort na 50 iteraties (voor de duidelijkheid is dit slechts een uittreksel; het volledige resultaat vindt u hier):

n	ongesorteerd	oplopend	aflopend
…	…	…	…
16,384	27,9 ms	26,8 ms	65,6 ms
32.768	108,0 ms	105,4 ms	265,4 ms
65.536	434,0 ms	424,3 ms	1.052,2 ms
131.072	1.729,8 ms	1.714,1 ms	4.209,9 ms
262.144	6.913,4 ms	6.880,2 ms	16.863,7 ms
524.288	27.649,8 ms	27.568,7 ms	67.537,8 ms

Hier nog eens de metingen als diagram (waarbij ik “ongesorteerd” en “oplopend” als één curve heb weergegeven vanwege de vrijwel identieke waarden):

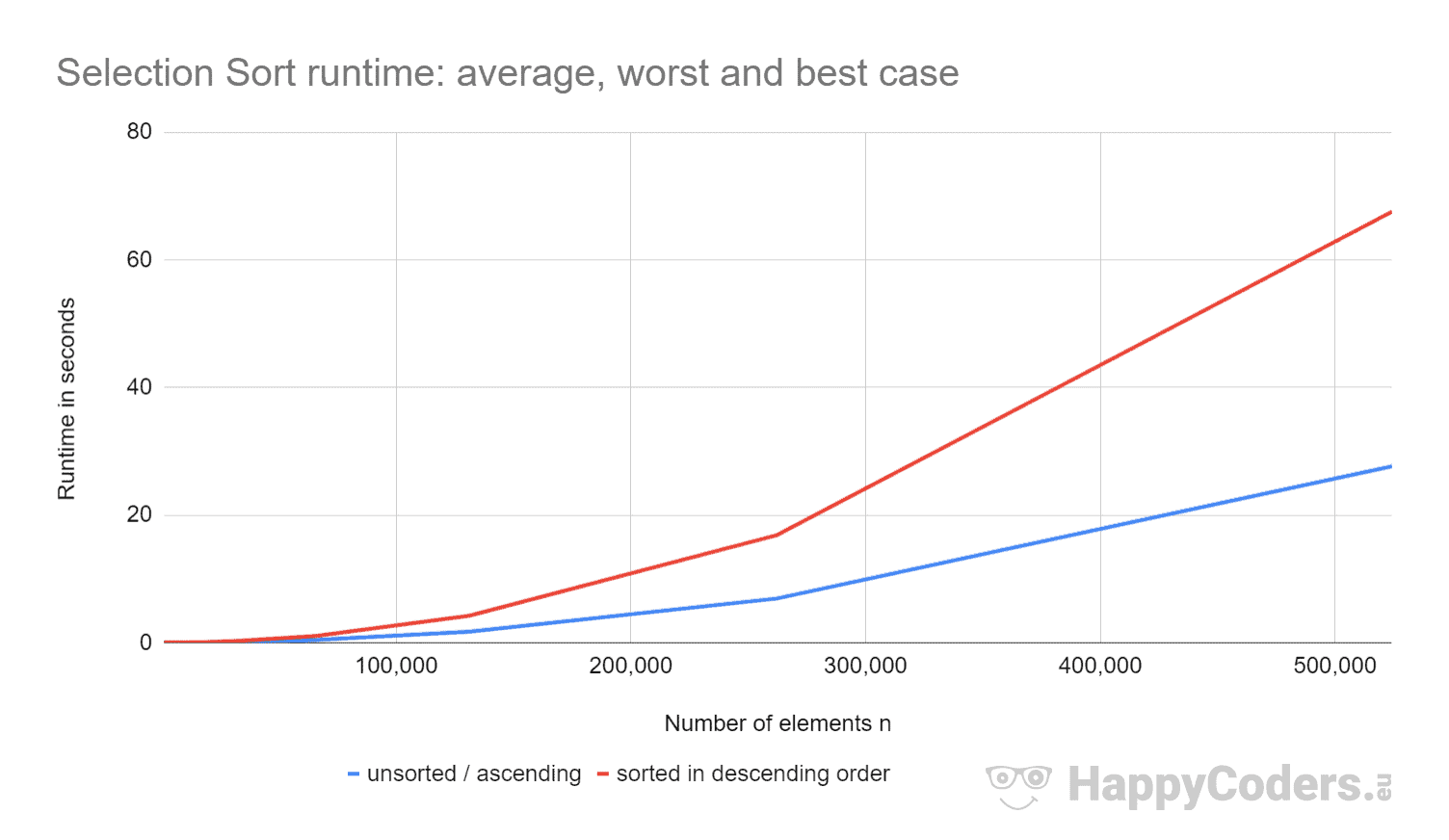
Het is goed te zien dat

• als het aantal elementen wordt verdubbeld, de runtime ongeveer verviervoudigd wordt – ongeacht of de elementen eerder gesorteerd zijn of niet. Dit komt overeen met de verwachte tijdcomplexiteit van O(n²).
• dat de runtime voor oplopende gesorteerde elementen iets beter is dan voor ongesorteerde elementen. Dit komt omdat de swap operaties, die – zoals hierboven geanalyseerd – van weinig belang zijn, hier niet nodig zijn.
• dat de runtime voor aflopende gesorteerde elementen significant slechter is dan voor ongesorteerde elementen.

Waarom?

Analysis of the Worst-Case Runtime

Theoretisch zou het zoeken naar het kleinste element altijd evenveel tijd moeten kosten, ongeacht de beginsituatie. En de verwissel operaties zouden alleen iets meer moeten zijn voor elementen gesorteerd in aflopende volgorde (voor elementen gesorteerd in aflopende volgorde, zou elk element verwisseld moeten worden; voor ongesorteerde elementen, zou bijna elk element verwisseld moeten worden).

Gebruik makend van het CountOperations programma uit mijn GitHub repository, kunnen we het aantal verschillende operaties zien. Hier zijn de resultaten voor ongesorteerde elementen en elementen gesorteerd in aflopende volgorde, samengevat in één tabel:

n	Vergelijkingen	Swaps ongesorteerd	Swaps aflopend	minPos/min ongesorteerd	minPos/min aflopend
…	…	…	…	…	…
512	130.816	504	256	2.866	66.047
1.024	523.776	1.017	512	6.439	263.167
2.048	2.096.128	2.042	1.024	14.727	1.050.623
4.096	8.386.560	4.084	2.048	30.758	4.198.399
8.192	33.550.336	8.181	4.096	69.378	16.785.407

Van de gemeten waarden kunnen we het volgende aflezen:

• Met elementen in aflopende volgorde gesorteerd, hebben we – zoals verwacht – evenveel vergelijkingsoperaties als met ongesorteerde elementen – dat wil zeggen, n × (n-1) / 2.
• Met ongesorteerde elementen hebben we – zoals verondersteld – bijna evenveel ruilbewerkingen als elementen: bijvoorbeeld, met 4.096 ongesorteerde elementen, zijn er 4.084 ruilbewerkingen. Deze aantallen veranderen willekeurig van test tot test.
• Maar met elementen gesorteerd in aflopende volgorde, hebben we slechts de helft van het aantal swap operaties als elementen! Dit komt omdat we bij het verwisselen niet alleen het kleinste element op de juiste plaats zetten, maar ook de betreffende verwisselpartner.

Met acht elementen hebben we bijvoorbeeld vier verwisseloperaties. In de eerste vier iteraties hebben we er telkens één en in de iteraties vijf tot en met acht geen (desondanks blijft het algoritme tot het einde doorlopen):

Verder kunnen we uit de metingen aflezen:

• De reden waarom Selection Sort zoveel langzamer is met elementen die in aflopende volgorde zijn gesorteerd, kan worden gevonden in het aantal lokale variabelentoewijzingen (minPos en min) bij het zoeken naar het kleinste element. Terwijl we met 8.192 ongesorteerde elementen 69.378 van deze toewijzingen hebben, zijn er met elementen die in aflopende volgorde zijn gesorteerd 16.785.407 van dergelijke toewijzingen – dat is 242 keer zo veel!

Waarom dit enorme verschil?

Analyse van de runtime van het zoeken naar het kleinste element

Voor elementen die in aflopende volgorde zijn gesorteerd, kan de orde van grootte worden afgeleid uit de illustratie hierboven. Het zoeken naar het kleinste element is beperkt tot de driehoek van de oranje en oranje-blauwe vakjes. In het bovenste oranje deel worden de getallen in elk vakje kleiner; in het rechter oranje-blauwe deel worden de getallen weer groter.

Toewijzingsbewerkingen vinden plaats in elk oranje vak en in het eerste van de oranje-blauwe vakken. Het aantal toewijzingsoperaties voor minPos en min is dus, figuurlijk gesproken, ongeveer “een kwart van het kwadraat” – wiskundig en precies is het ¼ n² + n – 1.

Voor ongesorteerde elementen zouden we veel dieper in de materie moeten doordringen. Dat zou niet alleen buiten het bestek van dit artikel vallen, maar ook buiten dat van de hele blog.

Daarom beperk ik mijn analyse tot een klein demoprogrammaatje dat meet hoeveel minPos/min-opdrachten er zijn bij het zoeken naar het kleinste element in een ongesorteerde array. Hier zijn de gemiddelde waarden na 100 iteraties (een klein uittreksel; de volledige resultaten zijn hier te vinden):

n	gemiddeld aantal minPos/min toewijzingen
1.024	7.08
4.096	8.61
16.385	8.94
65.536	11.81
262.144	12.22
1.048.576	14.26
4.194.304	14.71
16.777.216	16.44
67.108.864	17.92
268.435.456	20.27

Hier als diagram met logaritmische x-as:

De grafiek laat heel mooi zien dat we logaritmische groei hebben, d.w.z., bij elke verdubbeling van het aantal elementen neemt het aantal opdrachten slechts met een constante waarde toe. Zoals gezegd, zal ik niet dieper ingaan op wiskundige achtergronden.

Dit is de reden waarom deze minPos/min toewijzingen van weinig betekenis zijn in ongesorteerde arrays.

Andere kenmerken van Selection Sort

In de volgende secties zal ik de ruimtecomplexiteit, stabiliteit, en parallelliseerbaarheid van Selection Sort bespreken.

Ruimtecomplexiteit van Selection Sort

De ruimtecomplexiteit van Selection Sort is constant, omdat we geen extra geheugenruimte nodig hebben, afgezien van de lusvariabelen i en j en de hulpvariabelen length, minPos, en min.

Dat wil zeggen, het maakt niet uit hoeveel elementen we sorteren – tien of tien miljoen – we hebben altijd alleen deze vijf extra variabelen nodig. We noteren de constante tijd als O(1).

Stabiliteit van Selection Sort

Selection Sort lijkt op het eerste gezicht stabiel: Als het ongesorteerde deel meerdere elementen met dezelfde sleutel bevat, moeten de eerste eerst aan het gesorteerde deel worden toegevoegd.

Maar schijn bedriegt. Want door in de tweede deelstap van het algoritme twee elementen om te wisselen, kan het gebeuren dat bepaalde elementen in het ongesorteerde deel niet meer de oorspronkelijke volgorde hebben. Dit leidt er dan weer toe dat ze in het gesorteerde deel niet meer in de oorspronkelijke volgorde voorkomen.

Een voorbeeld kan heel eenvoudig worden geconstrueerd. Stel we hebben twee verschillende elementen met sleutel 2 en een met sleutel 1, als volgt gerangschikt, en sorteren ze vervolgens met Selection Sort:

In de eerste stap worden het eerste en het laatste element verwisseld. Zo komt het element “TWEE” achter het element “twee” te staan – de volgorde van beide elementen is verwisseld.

In de tweede stap vergelijkt het algoritme de twee achterste elementen. Beide hebben dezelfde sleutel, 2. Er wordt dus geen element verwisseld.

In de derde stap blijft er nog maar één element over; dit wordt automatisch als gesorteerd beschouwd.

De twee elementen met de sleutel 2 zijn dus verwisseld naar hun oorspronkelijke volgorde – het algoritme is onstabiel.

Stabiele variant van Selection Sort

Selection Sort kan stabiel worden gemaakt door in stap twee niet het kleinste element met het eerste te verwisselen, maar door alle elementen tussen het eerste en het kleinste element één positie naar rechts te verschuiven en het kleinste element aan het begin in te voegen.

Ondanks dat de tijdcomplexiteit door deze wijziging gelijk blijft, zullen de extra verschuivingen tot een aanzienlijke prestatievermindering leiden, althans wanneer we een array sorteren.

Met een gekoppelde lijst zou het knippen en plakken van het te sorteren element zonder noemenswaardig prestatieverlies kunnen worden gedaan.

Paralleliseerbaarheid van Selection Sort

We kunnen de buitenste lus niet parallelliseren, omdat deze bij elke iteratie de inhoud van de array verandert.

De binnenste lus (zoeken naar het kleinste element) kan worden geparallelliseerd door de array te verdelen, parallel in elke subarray naar het kleinste element te zoeken, en de tussenresultaten samen te voegen.

Selection Sort vs. Insertion Sort

Welk algoritme is sneller, Selection Sort, of Insertion Sort?

Laten we de metingen van mijn Java-implementaties eens vergelijken.

Ik laat het beste geval buiten beschouwing. Met Insertion Sort is de tijdcomplexiteit in het beste geval O(n) en duurde het minder dan een milliseconde voor maximaal 524.288 elementen. Dus in het beste geval is Insertion Sort, voor een willekeurig aantal elementen, ordes van grootte sneller dan Selection Sort.

n	Selection Sort unsorted	Insertion Sort unsorted	Selection Sort descending	Insertion Sort descending
…	…	…	…	…
16,384	27,9 ms	21,9 ms	65,6 ms	43,6 ms
32.768	108,0 ms	87,9 ms	265,4 ms	175,8 ms
65.536	434,0 ms	350,4 ms	1.052,2 ms	697,6 ms
131.072	1.729,8 ms	1.398,9 ms	4.209,9 ms	2.840,0 ms
262.144	6.913,4 ms	5.706,8 ms	16.863,7 ms	11.517,4 ms
524.288	27.649,8 ms	23.009,7 ms	67.537,8 ms	46,309,3 ms

En nogmaals als diagram:

Insertion Sort is dus niet alleen sneller dan Selection Sort in het beste geval, maar ook in het gemiddelde en in het slechtste geval.

De reden hiervoor is dat Insertion Sort gemiddeld half zo veel vergelijkingen vereist. Ter herinnering, met Insertion Sort hebben we vergelijkingen en verschuivingen gemiddeld tot de helft van de gesorteerde elementen; met Selection Sort moeten we in elke stap zoeken naar het kleinste element in alle ongesorteerde elementen.

Selection Sort heeft aanzienlijk minder schrijfoperaties, dus Selection Sort kan sneller zijn wanneer schrijfoperaties duur zijn. Dit is niet het geval bij sequentiële schrijfbewerkingen naar arrays, omdat deze meestal in de CPU-cache worden uitgevoerd.

In de praktijk wordt Selection Sort daarom bijna nooit gebruikt.

Samenvatting

Selection Sort is een eenvoudig te implementeren, en in zijn typische implementatie instabiel, sorteeralgoritme met een gemiddelde, best-case, en worst-case tijdcomplexiteit van O(n²).

Selection Sort is langzamer dan Insertion Sort, en wordt daarom in de praktijk zelden gebruikt.

Meer sorteeralgoritmen vindt u in dit overzicht van alle sorteeralgoritmen en hun eigenschappen in het eerste deel van de artikelenserie.

Als u het artikel leuk vond, voel u dan vrij om het te delen met behulp van een van de deelknoppen aan het eind. Wil je per e-mail op de hoogte gehouden worden wanneer ik een nieuw artikel publiceer? Gebruik dan het volgende formulier om u in te schrijven voor mijn nieuwsbrief.