Biografie
Johannes Kepler wordt nu vooral herinnerd vanwege de ontdekking van de drie wetten van de planetaire beweging die zijn naam dragen (gepubliceerd in 1609 en 1619). Hij verrichte ook belangrijk werk in de optica (1604, 1611), ontdekte twee nieuwe regelmatige veelvlakken (1619), gaf de eerste wiskundige behandeling van de nauwe pakking van gelijke bollen (wat leidde tot een verklaring van de vorm van de cellen van een honingraat, 1611), gaf het eerste bewijs van de werking van logaritmen (1624), en bedacht een methode om de volumes van vaste stoffen met een omwenteling te vinden die (achteraf gezien!) kan worden gezien als een bijdrage aan de ontwikkeling van de calculus (1615, 1616). Bovendien berekende hij de meest exacte astronomische tabellen tot nu toe bekend, waarvan de blijvende nauwkeurigheid veel heeft bijgedragen aan het vaststellen van de waarheid van de heliocentrische astronomie (Rudolphine Tables, Ulm, 1627).
Er is een grote hoeveelheid correspondentie van Kepler bewaard gebleven. Veel van zijn brieven zijn bijna het equivalent van een wetenschappelijk artikel (er waren nog geen wetenschappelijke tijdschriften), en correspondenten schijnen ze te hebben bewaard omdat ze interessant waren. Bijgevolg weten we vrij veel over het leven van Kepler, en zelfs over zijn karakter. Mede hierdoor heeft Kepler een carrière als min of meer fictief personage achter de rug (zie de historiografische noot hieronder).
Kinderjaren
Kepler werd geboren in het stadje Weil der Stadt in Zwaben en verhuisde in 1576 met zijn ouders naar het nabijgelegen Leonberg. Zijn vader was een huursoldaat en zijn moeder de dochter van een herbergier. Johannes was hun eerste kind. Zijn vader verliet het huis voor de laatste keer toen Johannes vijf jaar oud was, en men vermoedt dat hij in de oorlog in de Nederlanden is omgekomen. Als kind woonde Kepler met zijn moeder in de herberg van zijn grootvader. Hij vertelt dat hij vroeger hielp door in de herberg te bedienen. Men kan zich voorstellen dat de klanten soms verbijsterd waren over de ongewone vaardigheid van het kind in rekenen.
Keplers vroege opleiding genoot hij op een plaatselijke school en vervolgens op een nabijgelegen seminarie, waar hij zich, met de bedoeling om priester te worden, inschreef aan de Universiteit van Tübingen, toen (net als nu) een bolwerk van Lutherse orthodoxie.
De opvattingen van Kepler
Kepler was zijn hele leven lang een diepgelovig man. Al zijn geschriften bevatten talrijke verwijzingen naar God, en hij zag zijn werk als een vervulling van zijn christelijke plicht om de werken van God te begrijpen. Aangezien de mens, zoals Kepler geloofde, naar het beeld van God was geschapen, was hij duidelijk in staat het heelal te begrijpen dat Hij had geschapen. Bovendien was Kepler ervan overtuigd dat God het heelal had geschapen volgens een wiskundig plan (een overtuiging die men terugvindt in de werken van Plato en die in verband wordt gebracht met Pythagoras). Aangezien het in die tijd algemeen aanvaard was dat de wiskunde een veilige methode bood om tot waarheden over de wereld te komen (de algemene begrippen en postulaten van Euclides werden als werkelijk waar beschouwd), hebben we hier te maken met een strategie om het heelal te begrijpen. Aangezien sommige auteurs Kepler een naam van irrationaliteit hebben gegeven, is het de moeite waard op te merken dat deze nogal hoopvolle epistemologie wel erg ver afstaat van de overtuiging van de mysticus dat de dingen alleen begrepen kunnen worden op een onnauwkeurige manier die berust op inzichten die niet aan de rede onderworpen zijn. Kepler dankt inderdaad herhaaldelijk God dat Hij hem inzichten heeft geschonken, maar die inzichten worden als rationeel voorgesteld.
Universitair onderwijs
In die tijd was het gebruikelijk dat alle studenten aan een universiteit cursussen “wiskunde” volgden. In principe omvatte dit de vier wiskundige wetenschappen: rekenen, meetkunde, astronomie en muziek. Het lijkt er echter op dat het van de universiteit in kwestie afhing wat er werd onderwezen. In Tübingen kreeg Kepler les in astronomie van een van de belangrijkste astronomen van die tijd, Michael Mästlin (1550 – 1631). De astronomie van het leerplan was natuurlijk de geocentrische astronomie, dat wil zeggen de huidige versie van het Ptolemeïsche systeem, waarin alle zeven planeten – Maan, Mercurius, Venus, Zon, Mars, Jupiter en Saturnus – rond de Aarde bewogen en hun posities ten opzichte van de vaste sterren werden berekend door cirkelbewegingen te combineren. Dit systeem was min of meer in overeenstemming met de huidige (Aristotelische) opvattingen over natuurkunde, hoewel er bepaalde moeilijkheden waren, zoals de vraag of men een cirkelvormige beweging die niet uniform was rond zijn eigen middelpunt maar rond een ander punt (een “equant” genoemd) als “uniform” (en dus aanvaardbaar als kennelijk eeuwig) kon beschouwen. Het lijkt er echter op dat de astronomen (die zichzelf als “wiskundigen” beschouwden) over het algemeen genoegen namen met het berekenen van de posities van de planeten en het aan de natuurfilosofen overlieten om zich druk te maken over de vraag of de wiskundige modellen overeenkwamen met de natuurkundige mechanismen. Kepler nam deze houding niet aan. Zijn vroegst gepubliceerde werk (1596) stelt voor om de werkelijke banen van de planeten te beschouwen, niet de cirkels die gebruikt worden om ze te construeren.
In Tübingen studeerde Kepler niet alleen wiskunde, maar ook Grieks en Hebreeuws (beide noodzakelijk om de Schriften in hun oorspronkelijke taal te kunnen lezen). Het onderwijs werd gegeven in het Latijn. Aan het eind van zijn eerste jaar kreeg Kepler ‘A’s voor alles behalve wiskunde. Waarschijnlijk probeerde Mästlin hem duidelijk te maken dat hij beter kon, want Kepler behoorde tot de selecte groep leerlingen aan wie hij meer geavanceerde astronomie wilde leren door hen kennis te laten maken met het nieuwe, heliocentrische kosmologische systeem van Copernicus. Van Mästlin hoorde Kepler dat het voorwoord bij Over de omwentelingen, waarin werd uitgelegd dat het om “slechts wiskunde” ging, niet van Copernicus was. Kepler schijnt vrijwel onmiddellijk te hebben aanvaard dat het Copernicaanse systeem fysisch juist was; zijn redenen om het te aanvaarden zullen worden besproken in verband met zijn eerste kosmologische model (zie hieronder).
Het schijnt dat er zelfs in Keplers studententijd aanwijzingen waren dat zijn religieuze opvattingen niet geheel in overeenstemming waren met het orthodoxe lutheranisme dat in Tübingen gangbaar was en in de Confessio Augustana Ⓣ was geformuleerd. Keplers problemen met deze protestantse orthodoxie betroffen de veronderstelde relatie tussen materie en “geest” (een niet-materiële entiteit) in de leer van de Eucharistie. Dit hangt in zoverre samen met de astronomie van Kepler, dat hij blijkbaar soortgelijke intellectuele moeilijkheden ondervond om uit te leggen hoe “kracht” van de zon de planeten kon beïnvloeden. In zijn geschriften is Kepler geneigd zijn mening op het spel te zetten – wat historici goed uitkomt. In het echte leven lijkt het waarschijnlijk dat een soortgelijke neiging tot openheid de autoriteiten in Tübingen ertoe bracht gegronde twijfels te koesteren over zijn religieuze orthodoxie. Dit kan verklaren waarom Mästlin Kepler overhaalde om af te zien van zijn wijdingsplan en in plaats daarvan een post als wiskundeleraar in Graz te aanvaarden. De religieuze onverdraagzaamheid verscherpte zich in de daaropvolgende jaren. In 1612 werd Kepler geëxcommuniceerd. Dit deed hem veel pijn, maar ondanks zijn (toen) relatief hoge sociale status, als keizerlijk wiskundige, is het hem nooit gelukt om de ban opgeheven te krijgen.
Keplers eerste kosmologische model (1596)
In plaats van de zeven planeten in de standaard geocentrische astronomie had het Copernicaanse systeem er slechts zes, waarbij de Maan een tot dan toe onbekend hemellichaam was geworden, dat Kepler later een ‘satelliet’ zou noemen (een naam die hij in 1610 bedacht om de manen aan te duiden die Galileo had ontdekt in een baan rond Jupiter, en die letterlijk ‘begeleider’ betekent). Waarom zes planeten? Bovendien was het in de geocentrische astronomie niet mogelijk om met behulp van waarnemingen de relatieve grootte van de planeetbollen te bepalen; men ging er eenvoudigweg van uit dat ze met elkaar in contact stonden. Dit leek geen verklaring te behoeven, omdat het mooi aansloot bij het geloof van de natuurfilosofen dat het hele systeem werd gekeerd door de beweging van de buitenste bol, één (of misschien twee) voorbij de bol van de ‘vaste’ sterren (die waarvan het patroon de sterrenbeelden vormden), voorbij de bol van Saturnus. In het Copernicaanse systeem kon men, doordat de jaarlijkse component van de beweging van elke planeet een afspiegeling was van de jaarlijkse beweging van de Aarde, aan de hand van waarnemingen de omvang van de baan van elke planeet berekenen, en het bleek dat er enorme ruimten tussen de planeten waren. Waarom juist deze ruimtes?
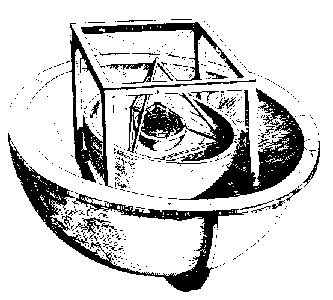
Keplers antwoord op deze vragen, beschreven in zijn Mysterium cosmographicum Ⓣ, Tübingen, 1596, komt op twintigste-eeuwse lezers bizar over (zie de figuur hiernaast). Hij stelde voor dat als een bol zo werd getekend dat hij de binnenkant van het pad van Saturnus raakte, en een kubus werd ingeschreven in de bol, dan zou de bol die in die kubus is ingeschreven de bol zijn die het pad van Jupiter omcirkelt. Als dan in de bol die het pad van Jupiter beschrijft een regelmatige tetraëder zou worden getekend, dan zou de inwendige sfeer van de tetraëder de bol zijn die het pad van Mars beschrijft, en zo verder naar binnen, zodat de regelmatige dodecaëder tussen Mars en de Aarde komt te staan, de regelmatige icosaëder tussen de Aarde en Venus, en de regelmatige octaëder tussen Venus en Mercurius. Dit verklaart het aantal planeten perfect: er zijn slechts vijf convexe regelmatige vaste lichamen (zoals wordt bewezen in Euclides’ Elementen , Boek 13). Het geeft ook een overtuigende fit met de grootte van de banen zoals afgeleid door Copernicus, waarbij de grootste fout minder dan 10% is (wat zelfs nu nog spectaculair goed is voor een kosmologisch model). Kepler drukte zich niet uit in termen van procentuele fouten, en zijn model is in feite het eerste wiskundige kosmologische model, maar het is gemakkelijk te zien waarom hij geloofde dat de waarnemingen zijn theorie ondersteunden.
Kepler zag zijn kosmologische theorie als een bewijs voor de Copernicaanse theorie. Voordat hij zijn eigen theorie presenteerde, gaf hij argumenten om de plausibiliteit van de Copernicaanse theorie zelf vast te stellen. Kepler beweert dat de voordelen van de Copernicaanse theorie ten opzichte van de geocentrische theorie gelegen zijn in de grotere verklarende kracht ervan. De copernicaanse theorie kan bijvoorbeeld verklaren waarom Venus en Mercurius nooit ver van de zon te zien zijn (ze liggen tussen de aarde en de zon), terwijl er in de geocentrische theorie geen verklaring voor dit feit is. Kepler somt negen van dergelijke vragen op in het eerste hoofdstuk van het Mysterium cosmographicum Ⓣ.
Kepler voerde dit werk uit terwijl hij in Graz les gaf, maar het boek werd in Tübingen door Mästlin door de pers gehaald. De overeenkomst met de uit waarnemingen afgeleide waarden was niet exact, en Kepler hoopte dat betere waarnemingen de overeenkomst zouden verbeteren, dus stuurde hij een exemplaar van het Mysterium cosmographicum naar een van de belangrijkste waarnemingsastronomen van die tijd, Tycho Brahe (1546 – 1601). Tycho, die toen in Praag werkte (in die tijd de hoofdstad van het Heilige Roomse Rijk), had in feite Mästlin al geschreven op zoek naar een wiskundig assistent. Kepler kreeg de baan.
De ‘Oorlog met Mars’
Natuurlijk genoeg waren Tycho’s prioriteiten niet dezelfde als die van Kepler, en Kepler werkte al snel aan het onoplosbare probleem van de baan van Mars. Hij bleef hieraan werken nadat Tycho was overleden (in 1601) en Kepler hem opvolgde als keizerlijk wiskundige. Conventioneel werden banen samengesteld uit cirkels, en er waren vrij weinig waarnemingswaarden nodig om de relatieve stralen en posities van de cirkels vast te stellen. Tycho had een enorm aantal waarnemingen gedaan en Kepler was vastbesloten er zo goed mogelijk gebruik van te maken. In feite had hij zoveel waarnemingen beschikbaar dat hij, wanneer hij eenmaal een mogelijke baan had geconstrueerd, deze aan verdere waarnemingen kon toetsen totdat bevredigende overeenstemming was bereikt. Kepler concludeerde dat de baan van Mars een ellips was met de Zon in een van de brandpunten (een resultaat dat, uitgebreid tot alle planeten, nu “de Eerste Wet van Kepler” wordt genoemd), en dat een lijn die de planeet met de Zon verbindt in gelijke tijden gelijke oppervlakten aflegde naarmate de planeet zijn baan beschreef (“de Tweede Wet van Kepler”), dat wil zeggen dat de oppervlakte als maat voor de tijd wordt gebruikt. Nadat dit werk was gepubliceerd in Astronomia nova, … Ⓣ, Heidelberg, 1609, vond Kepler banen voor de andere planeten, waarmee hij vaststelde dat de twee wetten ook voor hen golden. Beide wetten hebben betrekking op de beweging van de planeet ten opzichte van de Zon; Keplers Copernicanisme was van cruciaal belang voor zijn redenering en voor zijn deducties.
Het eigenlijke berekeningsproces voor Mars was enorm bewerkelijk – er zijn bijna duizend foliobladen met rekenwerk bewaard gebleven – en Kepler zelf noemt dit werk ‘mijn oorlog met Mars’, maar het resultaat was een baan die zo precies overeenkomt met moderne resultaten dat bij de vergelijking rekening moet worden gehouden met seculiere veranderingen in de baan sinds Keplers tijd.
Observatiefout
Het was voor Keplers methode om mogelijke banen te toetsen aan waarnemingen van cruciaal belang dat hij een idee had van wat als voldoende overeenstemming zou moeten worden aanvaard. Hieruit vloeit het eerste expliciete gebruik van het begrip “waarnemingsfout” voort. Kepler dankte dit begrip wellicht althans gedeeltelijk aan Tycho, die de prestaties van zijn instrumenten in detail controleerde (zie de biografie van Brahe).
Optica, en de nieuwe ster van 1604
Het werk aan Mars was in 1605 in hoofdzaak voltooid, maar er waren vertragingen bij het uitgeven van het boek. Ondertussen, in antwoord op de bezorgdheid over de verschillende schijnbare diameter van de maan wanneer rechtstreeks waargenomen en wanneer waargenomen met behulp van een camera obscura, Kepler deed wat werk op het gebied van optica, en kwam met de eerste juiste wiskundige theorie van de camera obscura en de eerste juiste uitleg van de werking van het menselijk oog, met een omgekeerd beeld gevormd op het netvlies. Deze resultaten werden gepubliceerd in Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ, Frankfurt, 1604. Hij schreef ook over de Nieuwe Ster van 1604, die nu meestal ‘Keplers supernova’ wordt genoemd, waarbij hij talrijke verklaringen verwierp en op een gegeven moment opmerkte dat deze ster natuurlijk gewoon een speciale schepping kon zijn ‘maar voor we zover komen denk ik dat we al het andere moeten proberen’ De stella nova Ⓣ, Praag, 1606, hoofdstuk 22, KGW 1, p. 257, regel 23.
Na Galileo’s gebruik van de telescoop bij de ontdekking van de manen van Jupiter, gepubliceerd in zijn Sidereal Messenger (Venetië, 1610), waarop Kepler een enthousiast antwoord had geschreven (1610), schreef Kepler een studie over de eigenschappen van lenzen (het eerste werk over optica) waarin hij een nieuw ontwerp van een telescoop voorstelde, gebruikmakend van twee convexe lenzen (Dioptrice, Praag, 1611). Dit ontwerp, waarbij het uiteindelijke beeld omgekeerd is, was zo succesvol dat het nu meestal niet Kepleriaanse telescoop wordt genoemd, maar eenvoudigweg astronomische telescoop.
Vertrek uit Praag naar Linz
Keplers jaren in Praag waren relatief vredig, en wetenschappelijk gezien uiterst productief. Zelfs als het slecht ging, heeft hij zich nooit door externe omstandigheden laten weerhouden om verder te werken. Eind 1611 begon het heel slecht te gaan. Eerst stierf zijn zeven jaar oude zoon. Kepler schreef aan een vriend dat deze dood bijzonder moeilijk te dragen was omdat het kind hem zo sterk aan zichzelf op die leeftijd deed denken. Daarna stierf Keplers vrouw. Toen moest keizer Rudolf, wiens gezondheid het begaf, aftreden ten gunste van zijn broer Matthias, die evenals Rudolf katholiek was, maar (in tegenstelling tot Rudolf) niet geloofde in tolerantie jegens protestanten. Kepler moest Praag verlaten. Voordat hij vertrok liet hij het lichaam van zijn vrouw overbrengen naar het graf van zijn zoon, en schreef een Latijns grafschrift voor hen. Hij verhuisde met zijn overgebleven kinderen naar Linz (nu in Oostenrijk).
Huwelijk en wijnvaten
Kepler schijnt zijn eerste vrouw, Barbara, uit liefde getrouwd te zijn (hoewel het huwelijk via een makelaar was gearrangeerd). Het tweede huwelijk, in 1613, was een kwestie van praktische noodzaak; hij had iemand nodig om voor de kinderen te zorgen. Keplers nieuwe vrouw, Susanna, kreeg een spoedcursus in Keplers karakter: in de inleidende brief bij het resulterende boek wordt uitgelegd dat hij tijdens de huwelijksfeesten merkte dat de volumes van wijnvaten werden geschat met behulp van een staaf die er diagonaal door het spongat in werd gestoken, en hij begon zich af te vragen hoe dat kon werken. Het resultaat was een studie over de volumes van omwentelende vaste stoffen Nova stereometria doliorum … Ⓣ, Linz, 1615, waarin Kepler, zich baserend op het werk van Archimedes, gebruik maakte van een resolutie in ‘indivisibles’. Deze methode werd later ontwikkeld door Bonaventura Cavalieri (ca. 1598 – 1647) en behoort tot de stamboom van de infinitesimaalrekening.
De Harmonie van de Wereld
Keplers hoofdtaak als keizerlijk wiskundige was het schrijven van astronomische tabellen, gebaseerd op Tycho’s waarnemingen, maar wat hij eigenlijk wilde doen was De Harmonie van de Wereld schrijven, sinds 1599 gepland als een uitwerking van zijn Mysterie van de Kosmos. Dit tweede werk over kosmologie (Harmonices mundi libri V Ⓣ, Linz, 1619) presenteert een meer uitgewerkt wiskundig model dan het eerdere, hoewel de veelvlakken er nog steeds zijn. De wiskunde in dit werk omvat de eerste systematische behandeling van vlakvullingen, een bewijs dat er slechts dertien convexe uniforme veelvlakken zijn (de vaste lichamen van Archimedes) en de eerste beschrijving van twee niet-convexe regelmatige veelvlakken (alle in boek 2). De Harmonie van de Wereld bevat ook wat nu bekend staat als de Derde Wet van Kepler, dat voor twee planeten de verhouding van de kwadraten van hun perioden gelijk zal zijn aan de verhouding van de kubussen van de gemiddelde stralen van hun banen. Vanaf de eerste had Kepler gezocht naar een regel die de grootte van de banen in verband bracht met de perioden, maar er was geen sprake van een langzame reeks stappen in de richting van deze wet zoals bij de andere twee het geval was geweest. Hoewel de Derde Wet een belangrijke rol speelt in enkele van de laatste delen van de gedrukte versie van de Harmonie van de Wereld, werd zij in feite pas ontdekt toen het werk al gedrukt was. Kepler maakte op het laatste moment nog wijzigingen. Hijzelf vertelt het verhaal van het uiteindelijke succes:
…en als u het precieze tijdstip wilt weten, het werd mentaal bedacht op 8 maart van dit jaar duizend zeshonderd en achttien, maar op ongelukkige wijze aan de berekening onderworpen, en daarom als vals verworpen, en tenslotte op 15 mei teruggekeerd en een nieuwe aanvalslinie aangenomen, bestormde het de duisternis van mijn geest. Zo sterk was de steun van de combinatie van mijn arbeid van zeventien jaar aan de waarnemingen van Brahe en de onderhavige studie, die samenvloeiden, dat ik aanvankelijk geloofde dat ik droomde, en dat ik mijn conclusie als een van mijn uitgangspunten aannam. Maar het is absoluut zeker en exact dat “de verhouding tussen de periodieke tijden van twee planeten precies de sesquialterate verhouding is van hun gemiddelde afstanden …”
(Harmonice mundi Boek 5, Hoofdstuk 3, trans. Aiton, Duncan and Field, p. 411).
Heksenproces
Terwijl Kepler aan zijn Harmonie van de Wereld werkte, werd zijn moeder aangeklaagd wegens hekserij. Hij riep de hulp in van de juridische faculteit in Tübingen. Katharina Kepler werd uiteindelijk vrijgelaten, althans gedeeltelijk als gevolg van technische bezwaren die voortkwamen uit het feit dat de autoriteiten niet de juiste juridische procedures volgden bij het gebruik van marteling. De overgeleverde documenten zijn huiveringwekkend. Kepler ging echter door met zijn werk. In de koets, op zijn reis naar Württemberg om zijn moeder te verdedigen, las hij een werk over muziektheorie van Vincenzo Galilei (ca. 1520 – 1591, Galileo’s vader), waarnaar veelvuldig wordt verwezen in De harmonie van de wereld.
Astronomische tabellen
Het berekenen van tabellen, het normale werk voor een astronoom, bracht altijd zwaar rekenwerk met zich mee. Kepler was dan ook opgetogen toen hij in 1616 Napiers werk over logaritmen (gepubliceerd in 1614) tegenkwam. Mästlin liet hem echter prompt weten dat het ongepast was dat een serieuze wiskundige zich verheugde over een eenvoudige rekenhulp en dat het onverstandig was om logaritmen te vertrouwen omdat niemand begreep hoe ze werkten. (Soortgelijke opmerkingen werden in het begin van de jaren zestig gemaakt over computers.) Keplers antwoord op het tweede bezwaar was dat hij een bewijs publiceerde van de werking van logaritmen, gebaseerd op een onberispelijk respectabele bron: Euclides’ Elementen Boek 5. Kepler berekende tabellen met logaritmen van acht cijfers, die werden gepubliceerd met de Rudolphine Tafels (Ulm, 1628). De astronomische tabellen maakten niet alleen gebruik van Tycho’s waarnemingen, maar ook van de eerste twee wetten van Kepler. Alle astronomische tabellen die gebruik maakten van nieuwe waarnemingen waren nauwkeurig gedurende de eerste paar jaar na publicatie. Opmerkelijk aan de Rudolphine tafels was dat ze tientallen jaren lang nauwkeurig bleken te zijn. En naarmate de jaren verstreken, werd de voortdurende nauwkeurigheid van de tabellen natuurlijk gezien als een argument voor de juistheid van de wetten van Kepler, en dus voor de juistheid van de heliocentrische astronomie. Keplers vervulling van zijn saaie officiële taak als keizerlijk wiskundige leidde tot de vervulling van zijn liefste wens, het helpen vestigen van het copernicanisme.
Wallenstein
Tegen de tijd dat de Rudolfijnse Tafelen werden gepubliceerd werkte Kepler in feite niet meer voor de keizer (hij had Linz in 1626 verlaten), maar voor Albrecht von Wallenstein (1583 – 1632), een van de weinige succesvolle militaire leiders in de Dertigjarige Oorlog (1618 – 1648).
Wallenstein verwachtte, net als keizer Rudolf, dat Kepler hem adviezen zou geven op basis van astrologie. Kepler moest natuurlijk gehoorzamen, maar wijst er herhaaldelijk op dat hij niet gelooft dat precieze voorspellingen kunnen worden gedaan. Zoals de meeste mensen uit die tijd aanvaardde Kepler het principe van de astrologie, dat hemellichamen invloed konden hebben op wat er op Aarde gebeurde (de duidelijkste voorbeelden zijn dat de Zon de seizoenen veroorzaakt en de Maan de getijden), maar als Copernicaan geloofde hij niet in de fysische werkelijkheid van de sterrenbeelden. Zijn astrologie was alleen gebaseerd op de hoeken tussen de posities van hemellichamen (‘astrologische aspecten’). Hij had een grote minachting voor de ingewikkelde systemen van de conventionele astrologie.
Overlijden
Kepler overleed in Regensburg, na een korte ziekte. Hij verbleef in de stad op weg om geld te innen dat hem verschuldigd was in verband met de Rudolphijnse Tafelen. Hij werd begraven in de plaatselijke kerk, maar deze werd in de loop van de Dertigjarige Oorlog verwoest en van de graftombe is niets overgebleven.
Historiografische noot
Er is soms veel ophef gemaakt over vermeende niet-rationele elementen in de wetenschappelijke activiteit van Kepler. Gelovige astrologen beweren vaak dat zijn werk een wetenschappelijk respectabel antecedent is voor hun eigen werk. Wijlen Arthur Koestler maakte in zijn invloedrijke Sleepwalkers van Keplers strijd met Mars een argument voor de inherente irrationaliteit van de moderne wetenschap. Er zijn veel stilzwijgende aanhangers van deze twee overtuigingen geweest. Beide zijn echter gebaseerd op een zeer gedeeltelijke lezing van het werk van Kepler. In het bijzonder lijkt Koestler niet de wiskundige expertise te hebben gehad om de procedures van Kepler te begrijpen. Nadere bestudering toont aan dat Koestler zich eenvoudigweg vergiste in zijn beoordeling.
Het werkelijk belangrijke niet-rationele element in het werk van Kepler is zijn Christendom. Keplers uitgebreide en succesvolle gebruik van wiskunde doet zijn werk ‘modern’ lijken, maar in feite hebben we te maken met een christelijke natuurfilosoof, voor wie het begrijpen van de aard van het heelal ook het begrijpen van de aard van zijn Schepper inhield.