Een vergelijking in de hellingsbegrenzingsvorm wordt geschreven als
$$y=mx+b$$
Waarbij m de helling van de lijn is en b het y-afsnijpunt. Je kunt deze vergelijking gebruiken om een vergelijking te schrijven als je de helling en het y-afsnijpunt weet.
Voorbeeld
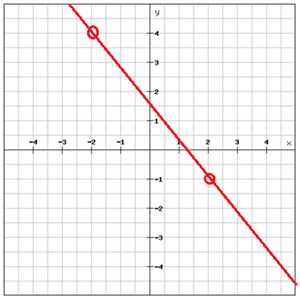
Vind de vergelijking van de lijn
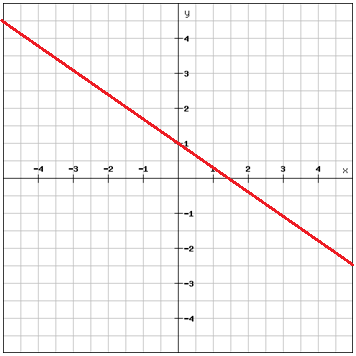
Kies twee punten die op de lijn liggen
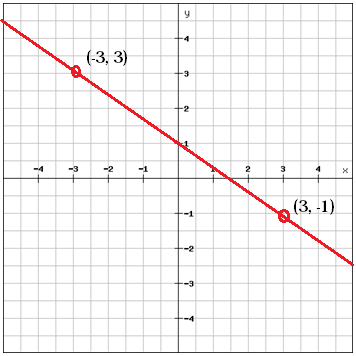
Bereken de helling tussen de twee punten
$m=\frac{y_{2}}, -y_{1}}{x_{2}}, -x_{1}}=\frac{links (-1}rechts )-3}{3- links ( -3}rechts )}=\frac{-4}{6}=\frac{-2}{3}$
We kunnen de b-waarde vinden, het y-afsnijpunt, door naar de grafiek te kijken
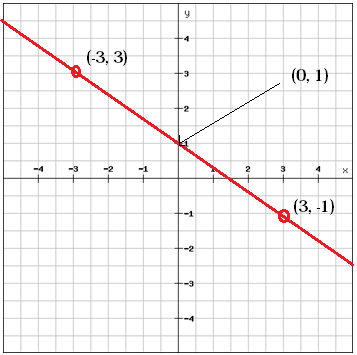
b = 1
We hebben een waarde voor m en een waarde voor b. Dit geeft ons de lineaire functie
$$y=-\frac{2}{3}x+1$$
In veel gevallen is de waarde van b niet zo gemakkelijk af te lezen. In die gevallen, of als je niet zeker weet of de rechte de y-as in dit specifieke punt wel kruist, kun je b berekenen door de vergelijking op te lossen voor b en dan x en y te vervangen door een van je twee punten.
We kunnen het bovenstaande voorbeeld gebruiken om dit te illustreren. We hebben de twee punten (-3, 3) en (3, -1). Uit deze twee punten hebben we de helling berekend
$m=-\frac{2}{3}$$
Dit geeft ons de vergelijking
$$y=-\frac{2}{3}x+b$$
Van hieruit kunnen we de vergelijking voor b oplossen
$b=y+\frac{2}{3}x$
En als we de waarden uit ons eerste punt (-3, 3) krijgen we
$b=3+\frac{2}{3}=3+\left ( -2 \right )=1$$
Als we deze waarde voor b in de vergelijking zetten krijgen we
$y=-\frac{2}{3}x+1$$
Dat is dezelfde vergelijking als toen we het y-afsnijpunt uit de grafiek afleidden.
Om samen te vatten hoe je een lineaire vergelijking schrijft met behulp van de helling-afsnijvorm, moet je
- De helling, m. bepalen. Dit kan door de helling tussen twee bekende punten van de lijn te berekenen met behulp van de hellingformule.
- Het y-afsnijpunt vinden. Dit kan door de helling en de coördinaten van een punt (x, y) op de lijn te substitueren in de helling-afbakeningsformule en dan op te lossen voor b.
Als je zowel m als b hebt, kun je ze gewoon op hun respectieve plaats in de vergelijking zetten.
Videoles
Vind de vergelijking met de grafiek