Blokcijferwerkingsmodus

Geauthenticeerde encryptie met aanvullende gegevens (AEAD) modiEdit

Er is een aantal werkwijzen ontworpen om geheimhouding en authenticatie in een enkele cryptografische primitieve te combineren. Voorbeelden van dergelijke modi zijn extended cipher block chaining (XCBC), integrity-aware cipher block chaining (IACBC), integrity-aware parallelizable mode (IAPM), OCB, EAX, CWC, CCM, en GCM. Geauthenticeerde versleutelingswijzen worden ingedeeld in single-passwijzen of double-passwijzen. Sommige single-pass geauthenticeerde versleutelingsalgoritmen, zoals de OCB-mode, zijn gepatenteerd, terwijl andere speciaal zijn ontworpen en uitgebracht om deze patenten te omzeilen.

Een aantal modi staat ook de authenticatie van niet-versleutelde geassocieerde gegevens toe, en deze worden AEAD-schema’s (authenticated encryption with associated data) genoemd. De EAX-mode is bijvoorbeeld een double-pass AEAD-regeling, terwijl de OCB-mode single-pass is.

Galois/counter (GCM)bewerken

GCM

Galois/counter

Encryptie paralleliseerbaar

Ja

Ontcijfering paralleliseerbaar

Ja

Random-leestoegang

Ja

Galois/counter mode (GCM) combineert de welbekendebekende tellermodus voor encryptie met de nieuwe Galois-modus voor authenticatie. De belangrijkste eigenschap is het gemak van parallelle berekening van de Galois-veldvermenigvuldiging die voor authenticatie wordt gebruikt. Deze eigenschap maakt een hogere verwerkingscapaciteit mogelijk dan versleutelingsalgoritmen.

GCM is gedefinieerd voor blokcijfers met een blokgrootte van 128 bits. Galois message authentication code (GMAC) is een variant van de GCM die alleen authenticatie mogelijk maakt en een incrementele berichtauthenticatiecode kan vormen. Zowel de GCM als de GMAC kunnen initialisatievectoren van willekeurige lengte accepteren. GCM kan ten volle profiteren van parallelle verwerking en bij de implementatie van GCM kan efficiënt gebruik worden gemaakt van een instructiepijplijn of een hardwarepijplijn. Bij de CBC-werkwijze treden pijplijnstoringen op die de efficiëntie en prestaties belemmeren.

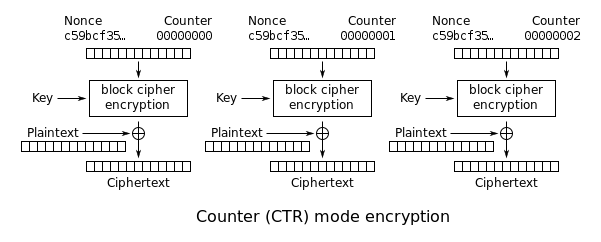
Net als bij CTR worden blokken opeenvolgend genummerd, waarna dit bloknummer wordt gecombineerd met een IV en versleuteld met een blokcijfer E, meestal AES. Het resultaat van deze encryptie wordt dan XORed met de klare tekst om de cijfertekst te produceren. Zoals alle tellermodi is dit in wezen een stroomcijfer en daarom is het van essentieel belang dat voor elke stroom die wordt versleuteld een andere IV wordt gebruikt.

De cijfertekstblokken worden beschouwd als coëfficiënten van een polynoom die vervolgens op een sleutelafhankelijk punt H wordt geëvalueerd met eindige-veldaritmetiek. Het resultaat wordt dan versleuteld, waarbij een authenticatietag wordt geproduceerd die kan worden gebruikt om de integriteit van de gegevens te verifiëren. De versleutelde tekst bevat dan de IV, de cijfertekst en het authenticatieplaatje.

Teller met cipher block chaining message authentication code (CCM)

Teller met cipher block chaining message authentication code (teller met CBC-MAC; CCM) is een geauthenticeerd versleutelingsalgoritme dat is ontworpen om zowel authenticatie als vertrouwelijkheid te verschaffen. CCM mode is alleen gedefinieerd voor blokcijfers met een bloklengte van 128 bits.

Synthetische initialisatie vector (SIV)Edit

Synthetische initialisatie vector (SIV) is een niet-ce-misbruik bestendige blokcijfer mode.

SIV synthetiseert een interne IV met behulp van de een pseudorandom functie S2V. S2V is een hash op basis van CMAC, en de input voor de functie is:

• Extra geauthenticeerde gegevens (nul, een of veel AAD-velden worden ondersteund)
• Plaintext
• Authenticatiesleutel (K1).

SIV codeert de S2V output en de klare tekst met AES-CTR, gesleuteld met de encryptie sleutel (K2).

SIV kan externe niet-ce-gebaseerde geauthenticeerde encryptie ondersteunen, in welk geval één van de geauthenticeerde data velden voor dit doel wordt gebruikt. RFC5297 specificeert dat voor interoperabiliteitsdoeleinden het laatste geauthenticeerde gegevensveld externe nonce moet worden gebruikt.

Door het gebruik van twee sleutels, de authenticatiesleutel K1 en de encryptiesleutel K2, kunnen naamgevingsschema’s voor SIV AEAD-varianten tot enige verwarring leiden; AEAD_AES_SIV_CMAC_256 verwijst bijvoorbeeld naar AES-SIV met twee AES-128 sleutels en niet AES-256.

AES-GCM-SIVEdit

AES-GCM-SIV is een bedrijfsmodus voor de Advanced Encryption Standard die vergelijkbare prestaties levert als de Galois/counter-modus en tevens bestand is tegen misbruik in het geval van het hergebruik van een cryptografische nonce. De constructie is gedefinieerd in RFC 8452.

AES-GCM-SIV synthetiseert de interne IV. Het leidt een hash af van de extra geauthenticeerde gegevens en de klare tekst met behulp van de POLYVAL Galois hashfunctie. De hash wordt vervolgens versleuteld met een AES-sleutel, en gebruikt als authenticatie-tag en AES-CTR-initialisatievector.

AES-GCM-SIV is een verbetering ten opzichte van het algoritme GCM-SIV, dat een zeer gelijkaardige naam heeft, met een paar zeer kleine veranderingen (b.v. hoe AES-CTR wordt geïnitialiseerd), maar die praktische voordelen oplevert voor de veiligheid “Deze toevoeging maakt het mogelijk om tot 250 berichten te versleutelen met dezelfde sleutel, vergeleken met de aanzienlijke beperking van slechts 232 berichten die waren toegestaan met GCM-SIV.”

Alleen vertrouwelijkheidsmodiEdit

Er zijn vele werkingsmodi gedefinieerd. Sommige daarvan worden hieronder beschreven. Het doel van cijfermodi is het maskeren van patronen die bestaan in gecodeerde gegevens, zoals geïllustreerd in de beschrijving van de zwakte van ECB.

De verschillende cijfermodi maskeren patronen door cascadering van de outputs van het cijfermatige blok of andere globaal deterministische variabelen in het volgende cijfermatige blok. De ingangen van de genoemde modi zijn in de volgende tabel samengevat:

Samenvatting van de modi

Mode		Formules	Cijfertekst
Elektronisch codeboek	(ECB)	Yi = F(PlainTexti, Key)	Yi
Cipher block chaining	(CBC)	Yi = PlainTexti XOR Ciphertexti-1	F(Y, Key); Cijfertekst0 = IV
Propagerende CBC	(PCBC)	Yi = PlainTexti XOR (Cijferteksti-1 XOR PlainTexti-1)	F(Y, sleutel); Cijfertekst0 = IV
Cijferfeedback	(CFB)	Yi = Cijferteksti-1	Plaintext XOR F(Y, Sleutel); Cijfertekst0 = IV
Output feedback	(OFB)	Yi = F(Yi-1, Sleutel); Y0 = F(IV, Sleutel)	Plaintext XOR Yi
Teller	(CTR)	Yi = F(IV + g(i), Sleutel); IV = token()	Plaintext XOR Yi

Noot: g(i) is een willekeurige deterministische functie, vaak de identiteitsfunctie.

Elektronisch codeboek (ECB)bewerken

ECB

Elektronisch codeboek

Encryptie paralleliseerbaar

Ja

Decryptie paralleliseerbaar

Ja

Random leestoegang

Ja

De eenvoudigste van de versleutelingswijzen is de elektronische codeboekwijze (ECB) (genoemd naar conventionele fysieke codeboeken). Het bericht wordt in blokken verdeeld, en elk blok wordt afzonderlijk versleuteld.

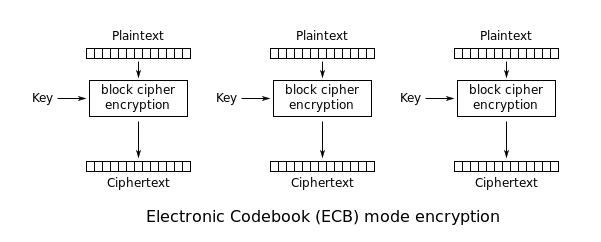
Het nadeel van deze methode is een gebrek aan diffusie. Omdat ECB identieke platte tekstblokken in identieke cijfertekstblokken codeert, worden gegevenspatronen niet goed verborgen.ECB wordt niet aanbevolen voor gebruik in cryptografische protocollen.

Een treffend voorbeeld van de mate waarin ECB datapatronen in de cijfertekst kan achterlaten, kan worden gezien wanneer de ECB-modus wordt gebruikt om een bitmap-afbeelding te coderen die grote gebieden met uniforme kleuren gebruikt. Hoewel de kleur van elke individuele pixel is gecodeerd, kan het beeld als geheel nog steeds worden onderscheiden, aangezien het patroon van identiek gekleurde pixels in het origineel in de gecodeerde versie blijft bestaan.

ECB-modus kan ook protocollen zonder integriteitsbescherming nog gevoeliger maken voor replay-aanvallen, aangezien elk blok op precies dezelfde manier wordt gedecodeerd.

Cipher block chaining (CBC)bewerken

CBC

Cipher block chaining

Encryptie paralleliseerbaar

Nee

Decryptie paralleliseerbaar

Ja

Random leestoegang

Ja

Ehrsam, Meyer, Smith en Tuchman hebben in 1976 de cipher block chaining (CBC)-modus uitgevonden. Bij CBC wordt elk onbewerkt tekstblok vóór de encryptie ge-XOR-ed met het voorgaande cijfertekstblok. Op deze manier is elk cijfertekstblok afhankelijk van alle platte tekstblokken die tot dan toe zijn verwerkt. Om elk bericht uniek te maken, moet in het eerste blok een initialisatievector worden gebruikt.

Als het eerste blok index 1 heeft, is de wiskundige formule voor CBC-versleuteling

C i = E K ( P i ⊕ C i – 1 ) , {displaystyle C_{i}=E_{K}(P_{i}}oplus C_{i-1}),}

C 0 = I V , {\displaystyle C_{0}=IV,}

terwijl de wiskundige formule voor CBC-decodering is

P i = D K ( C i ) ⊕ C i – 1 , {\displaystyle P_{i}=D_{K}(C_{i})\oplus C_{i-1},}

C 0 = I V . {Displaystyle C_{0}=IV.}

ExampleEdit

CBC is de meest gebruikte werkwijze geweest. De belangrijkste nadelen zijn dat de vercijfering sequentieel is (d.w.z. niet paralleliseerbaar), en dat het bericht moet worden opgevuld tot een veelvoud van de blokgrootte van de vercijfering. Een manier om dit laatste probleem op te lossen is de methode die bekend staat als cijfertekst stelen. Merk op dat een één-bits verandering in een klaartekst of initialisatie vector (IV) van invloed is op alle volgende cijfertekst blokken.

Versleutelen met de onjuiste IV zorgt ervoor dat het eerste blok klaartekst corrupt is, maar de volgende blokken klaartekst zullen correct zijn. Dit komt omdat elk blok wordt ge-XORed met de cijfertekst van het vorige blok, niet de klare tekst, zodat men het vorige blok niet hoeft te ontcijferen alvorens het te gebruiken als IV voor de ontcijfering van het huidige blok. Dit betekent dat een onbewerkt blok kan worden teruggevonden uit twee aangrenzende blokken cijfertekst. Als gevolg hiervan kan de ontcijfering worden geparallelliseerd. Merk op dat een verandering van één bit in de cijfertekst het corresponderende blok platte tekst volledig beschadigt en het corresponderende bit in het volgende blok platte tekst omkeert, maar dat de rest van de blokken intact blijft. Deze eigenaardigheid wordt gebruikt in verschillende padding oracle aanvallen, zoals POODLE.

Explicit initialization vectors maakt gebruik van deze eigenschap door een enkel willekeurig blok aan de klare tekst toe te voegen. Encryptie gebeurt zoals normaal, behalve dat het IV niet hoeft te worden doorgegeven aan de decryptie routine. Welk IV de ontcijfering ook gebruikt, alleen het willekeurige blok is “beschadigd”. Het kan veilig worden weggegooid en de rest van de ontcijfering is de originele klare tekst.

Propagating cipher block chaining (PCBC)bewerken

PCBC

Propagating cipher block chaining

Encryptie paralleliseerbaar

Nee

Decryptie parallelizable

Nee

Random-leestoegang

Nee

De propagating cipher block chaining of plaintext cipher-blokketenmodus is ontworpen om kleine veranderingen in de cijfertekst oneindig door te laten gaan bij het ontcijferen, als bij het vercijferen. In PCBC-modus wordt elk blok klaartekst XOR-gekoppeld met zowel het vorige klaartekstblok als het vorige cijfertekstblok alvorens te worden vercijferd. Net als in de CBC-modus wordt in het eerste blok een initialisatievector gebruikt.

Encryptie- en decryptie-algoritmen zijn als volgt:

C i = E K ( P i ⊕ P i – 1 ⊕ C i – 1 ) , P 0 ⊕ C 0 = I V , {\displaystyle C_{i}=E_{K}(P_{i}}oplus P_{i-1}oplus C_{i-1}),P_{0}oplus C_{0}=IV,}

P i = D K ( C i ) ⊕ P i – 1 ⊕ C i – 1 , P 0 ⊕ C 0 = I V . {Displaystyle P_{i}=D_{K}(C_{i})\oplus P_{i-1}\oplus C_{i-1},P_{0}\oplus C_{0}=IV.}

PCBC wordt met name gebruikt in Kerberos v4 en WASTE, maar is verder niet gebruikelijk. Als bij een in PCBC-modus gecodeerd bericht twee aangrenzende cijfertekstblokken worden uitgewisseld, heeft dit geen gevolgen voor de ontcijfering van de volgende blokken. Om deze reden wordt PCBC niet gebruikt in Kerberos v5.

Cijferkoppeling (CFB)bewerken

Vol-blok CFBEdit

CFB

Cijferfeedback

Encryptie paralleliseerbaar

Nee

Decryptie paralleliseerbaar

Ja

Random leestoegang

Ja

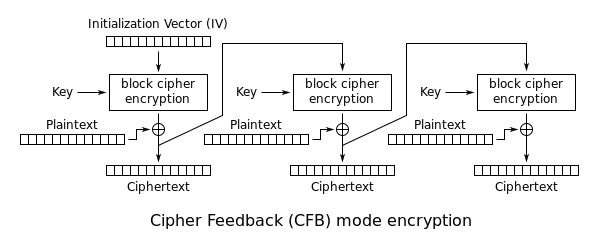
De modus cipher feedback (CFB), in zijn eenvoudigste vorm is het gebruik van de volledige uitvoer van het blokcijfer. In deze variatie, die erg lijkt op CBC, wordt van een blokcijfer een zelf-synchroniserend stroomcijfer gemaakt. CFB-decodering in deze variatie is bijna identiek aan CBC-codering in omgekeerde volgorde:

C i = { IV , i = 0 E K ( C i – 1 ) ⊕ P i , anders P i = E K ( C i – 1 ) ⊕ C i , {\displaystyle {begin{aligned}C_{i}&={text{IV}},&i=0\\E_{K}(C_{i-1})\oplus P_{i},&{\text{otherwise}}\end{cases}}\\P_{i}&=E_{K}(C_{i-1})\oplus C_{i},\end{aligned}}}

CFB-1, CFB-8, CFB-64, CFB-128, etc.Edit

NIST SP800-38A definieert CFB met een bit-breedte. De CFB-modus vereist ook een geheel getal, aangeduid als s, zodanig dat 1 ≤ s ≤ b. In de onderstaande specificatie van de CFB-modus bestaat elk klaartekstsegment (Pj) en cijfertekstsegment (Cj) uit s bits. De waarde van s wordt soms opgenomen in de naam van de modus, bijvoorbeeld de 1-bit CFB-modus, de 8-bit CFB-modus, de 64-bit CFB-modus of de 128-bit CFB-modus.

Deze modi zullen de uitvoer van het onderliggende blokcijfer inkorten.

I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}

I i = ( ( I i – 1 ≪ s ) + C i ) mod 2 b , {\displaystyle I_{i}={\big (}(I_{i-1})+C_{i}{\big )}{\bmod {2}^{b},}

C i = MSB s ( E K ( I i – 1 ) ) ⊕ P i , {Displaystyle C_{i}= {MSB} _{s}{E_{K}(I_{i-1}){\big )} P_{i},}

P i = MSB s ( E K ( I i – 1 ) ) ⊕ C i , {Displaystyle P_{i}= {MSB} _{s}{E_{K}(I_{i-1}){\big )},}

CFB-1 wordt beschouwd als zelf-synchroniserend en bestand tegen verlies van cijfertekst; “Als de 1-bit CFB-modus wordt gebruikt, dan wordt de synchronisatie automatisch hersteld b+1 posities na het ingevoegde of verwijderde bit. Voor andere waarden van s in de CFB-modus, en voor de andere vertrouwelijkheidsmodi in deze aanbeveling, moet de synchronisatie extern worden hersteld.” (NIST SP800-38A). D.w.z. 1-bit verlies in een 128-bit breed blokcijfer zoals AES zal 129 ongeldige bits maken alvorens geldige bits uit te zenden.

CFB kan ook zelf synchroniseren in sommige speciale gevallen anders dan gespecificeerd. Bijvoorbeeld, een verandering van één bit in CFB-128 met een onderliggend 128 bit blokcijfer, zal na twee blokken hersynchroniseren. (Echter, CFB-128 etc zal niet netjes omgaan met bit verlies; een verlies van één bit zal de decryptor doen uitlijnen met de encryptor)

CFB vergeleken met andere modesEdit

Zoals CBC mode, veranderingen in de klare tekst verspreiden zich voor altijd in de cijfertekst, en encryptie kan niet worden geparallelliseerd. Net als bij CBC kan ontcijfering parallel geschieden.

CFB, OFB en CTR hebben twee voordelen boven CBC: het blokcijfer wordt alleen in de vercijferende richting gebruikt, en het bericht hoeft niet te worden opgevuld tot een veelvoud van de blokgrootte van het cijfer (hoewel het stelen van cijfertekst ook bij CBC kan worden gebruikt om opvulling overbodig te maken).

Uitgangs-feedback (OFB)bewerken

OFB

Uitgangs-feedback

Encryptie paralleliseerbaar

Nee

Decryptie paralleliseerbaar

Nee

Random leestoegang

Nee

De modus uitvoerfeedback (OFB) maakt van een blokcijfer een synchroon stroomcijfer. Het genereert sleutelblokken die vervolgens worden ge-XOR-ed met de klare tekstblokken om de cijfertekst te verkrijgen. Net als bij andere stroomcijfers geeft het omdraaien van een bit in de cijfertekst een omgedraaid bit in de klare tekst op dezelfde plaats. Door deze eigenschap kunnen veel foutcorrigerende codes normaal functioneren, zelfs wanneer zij vóór de vercijfering worden toegepast.

Omwille van de symmetrie van de XOR-bewerking zijn vercijfering en ontcijfering precies hetzelfde:

C j = P j ⊕ O j , {displaystyle C_{j}=P_{j}\oplus O_{j},}

P j = C j ⊕ O j , {displaystyle P_{j}=C_{j}\oplus O_{j},}

O j = E K ( I j ) , {\displaystyle O_{j}=E_{K}(I_{j}),}

I j = O j – 1 , {\displaystyle I_{j}=O_{j-1},}

I 0 = IV . {\displaystyle I_{0}={\text{IV}}.}

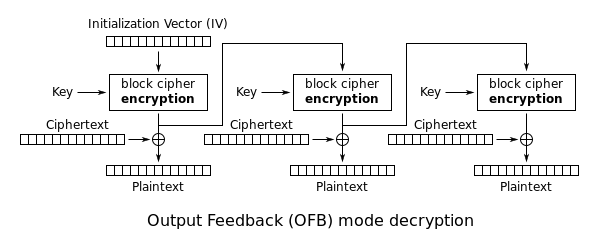
Elke output feedback blokcijferbewerking hangt af van alle voorgaande en kan dus niet parallel worden uitgevoerd. Omdat de klare tekst of cijfertekst alleen voor de laatste XOR wordt gebruikt, kunnen de blokcijferbewerkingen echter van tevoren worden uitgevoerd, zodat de laatste stap parallel kan worden uitgevoerd zodra de klare tekst of cijfertekst beschikbaar is.

Het is mogelijk een OFB mode keystream te verkrijgen door CBC mode te gebruiken met een constante reeks nullen als invoer. Dit kan nuttig zijn, omdat hierdoor snelle hardware-implementaties van de CBC-modus voor OFB-modus-versleuteling kunnen worden gebruikt.

Gebruik van de OFB-modus met een gedeeltelijk blok als feedback, zoals bij de CFB-modus, vermindert de gemiddelde cycluslengte met een factor 232 of meer. Een door Davies en Parkin voorgesteld wiskundig model, dat door experimentele resultaten wordt gestaafd, toont aan dat alleen met volledige terugkoppeling een gemiddelde cycluslengte kan worden bereikt die het bereikbare maximum benadert. Om deze reden werd de ondersteuning voor afgeknotte terugkoppeling uit de specificatie van OFB geschrapt.

Teller (CTR)bewerken

CTR

Counter

Vercijfering paralleliseerbaar

Ja

Decryptie paralleliseerbaar

Ja

Random leestoegang

Ja

Noot: CTR-modus (CM) is ook bekend als integer counter-modus (ICM) en gesegmenteerde integer counter-modus (SIC).

Net als OFB verandert de tellermodus een blokcijfer in een stroomcijfer. Het volgende sleutelblok wordt gegenereerd door opeenvolgende waarden van een “teller” te vercijferen. De teller kan om het even welke functie zijn die een sequentie produceert die gegarandeerd niet gedurende lange tijd herhaald zal worden, hoewel een increment-by-one teller de eenvoudigste en meest populaire is. Het gebruik van een eenvoudige deterministische invoerfunctie was vroeger controversieel; critici voerden aan dat “het opzettelijk blootstellen van een cryptosysteem aan een bekende systematische invoer een onnodig risico inhoudt”. Tegenwoordig wordt de CTR-mode echter algemeen aanvaard en worden eventuele problemen beschouwd als een zwakte van het onderliggende blokcijfer, dat geacht wordt veilig te zijn ongeacht de systematische vertekening van zijn invoer. Samen met CBC is de CTR modus één van de twee blokcijfermodi die worden aanbevolen door Niels Ferguson en Bruce Schneier.

CTR modus werd geïntroduceerd door Whitfield Diffie en Martin Hellman in 1979.

CTR modus heeft soortgelijke kenmerken als OFB, maar staat ook een willekeurige toegangseigenschap toe tijdens de ontcijfering. CTR mode is zeer geschikt om te werken op een multi-processor machine waar blokken parallel kunnen worden gecodeerd. Bovendien heeft het geen last van het kort-cyclisch probleem dat OFB kan hebben.

Als de IV/nonce willekeurig is, dan kunnen zij samen met de teller worden gecombineerd met behulp van elke inverteerbare bewerking (aaneenschakeling, optelling, of XOR) om het eigenlijke unieke tellerblok voor encryptie te produceren. In geval van een niet-willekeurige nonce (zoals een pakketteller) moeten de nonce en de teller aan elkaar worden gekoppeld (bv. door de nonce op te slaan in de bovenste 64 bits en de teller in de onderste 64 bits van een 128-bits tellerblok). Het eenvoudig optellen of XOR-en van de nonce en de teller tot één waarde zou in veel gevallen de beveiliging onder een “chosen-plaintext”-aanval verbreken, aangezien de aanvaller in staat zou kunnen zijn het gehele IV-tellerpaar te manipuleren om een botsing te veroorzaken. Zodra een aanvaller het IV-tellerpaar en de klare tekst controleert, zou XOR van de cijfertekst met de bekende klare tekst een waarde opleveren die, wanneer XOR-geteld met de cijfertekst van het andere blok dat hetzelfde IV-tellerpaar deelt, dat blok zou ontcijferen.

Merk op dat de nonce in dit diagram equivalent is aan de initialisatievector (IV) in de andere diagrammen. Als de offset/locatie-informatie echter corrupt is, zal het onmogelijk zijn om dergelijke gegevens gedeeltelijk te herstellen vanwege de afhankelijkheid van de byte-offset.