slope-intercept形式の方程式は
$y=mx+b$
ここでmは線の傾き、bはy切片である。 傾きとy切片が分かれば、この式を使って方程式を書くことができます。
例題
直線の方程式を求める
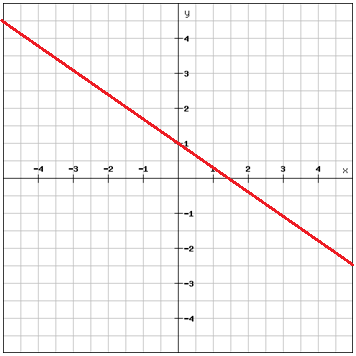
直線上の2点を選ぶ
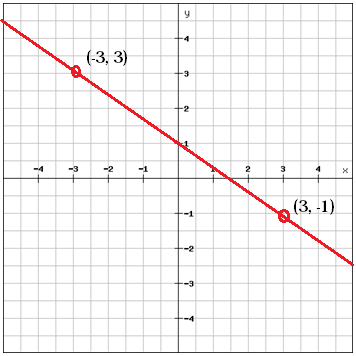
2点間の傾きを計算
$m=thefrac{y_{2}}, -y_{1}}{x_{2}} ╱。 -x_{1}}=hrac{pleft (-1 \right )-3}{3-appleft ( -3 \right )}=hrac{-4}{6}=hrac{-2}{3}$
b値を求めることができる。 y切片は、グラフ
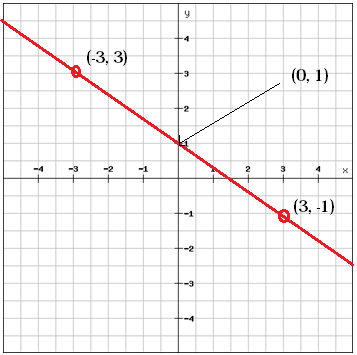
b = 1
mの値とbの値が得られましたね。 これで、1次関数
$y=-frac{2}{3}x+1$$
多くの場合、bの値は簡単に読み取れません。 そのような場合、または線が実際にこの特定の点で y 軸と交差しているかどうかが不確かな場合は、b の方程式を解いて x と y を 2 点のうちの 1 つに代入することで b を計算できます。
上の例を使って説明します。 (-3, 3)と(3, -1)の2点を用意しました。 この2点から、傾き
$m=-efficient{2}{3}$$ を計算すると、方程式
$y=-quality{3}$$ が得られます。\frac{2}{3}x+b$$
ここからbの式を解くと
$b=y+frac{2}{3}x$
そして最初の点の値を入れると(-3, 3)となり、
$b=3+frac{2}{3}cdot \left ( -3 \right )=3+left ( -2 \right )=1$
このbの値を式に入れると、
$y=- となります。\frac{2}{3}x+1$$
これは、グラフからy切片を読み取ったときの式と同じです。
傾き-切片の形式を使った連立方程式の書き方をまとめると
- 傾き m を求める。これは、傾きの公式を使って直線の既知の2点間の傾きを計算すればよい。 これは傾きと直線上の点(x, y)の座標を傾き-切片の式に代入し、bについて解くことでできます。
mとbの両方を得たら、それぞれの位置で方程式に入れるだけです。
ビデオレッスン
グラフに方程式を求める
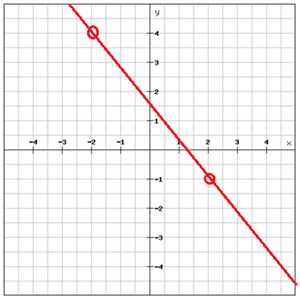
。