Biography
ヨハネス・ケプラーは、1609年と1619年に自分の名を冠した惑星運動の三法則を発見したことで主に記憶されている。) また、光学の分野でも重要な仕事をし(1604年、1611年)、2つの新しい正多面体を発見し(1619年)、等球の密充填を初めて数学的に扱い(ハニカムの細胞の形の説明につながる、1611年)、対数の働きを初めて証明し(1624年)、(今になってみれば!)微積分の発展に寄与したと見られる回転立体の体積を求める方法を考案した(1615年、1616年)。 さらに、それまで知られていた中で最も正確な天文表を計算し、その正確さが継続することで、地動説的天文学の真実が確立された(Rudolphine Tables, Ulm, 1627)<2659>ケプラーの書簡は大量に残されている。 ケプラーの手紙の多くは、科学論文に近いものであり(当時は科学雑誌がなかった)、文通相手はそれが面白いからということで残していたようである。 その結果、ケプラーの人生、そして彼の性格について多くのことを知ることができるのである。 そのため、ケプラーは多かれ少なかれ架空の人物として扱われてきた(下記の歴史学的注を参照)。 父親は傭兵、母親は宿屋の娘であった。 ヨハネスは二人の最初の子供だった。 父はヨハネスが5歳の時に家を出たのが最後で、オランダでの戦争で死んだと考えられている。 ケプラーは幼い頃、母親と一緒に祖父の経営する宿屋で暮らした。 ケプラーは幼い頃、祖父の経営する宿屋で母と暮らしていた。 ケプラーの幼少期の教育は、地元の学校と近くの神学校で行われ、そこから聖職に就くために、当時(現在も)ルター派正統派の砦であるチュービンゲン大学へ入学した。 彼の著作には神への言及が多く、自分の仕事は神の仕事を理解するキリスト教的義務の遂行であると考えた。 ケプラーは、人間は神に似せて作られた存在であり、神が創造した宇宙を理解することができると信じていた。 さらに、ケプラーは、神が数学的な計画に基づいて宇宙を作ったと確信していた(プラトンやピタゴラスの著作に見られる信念)。 当時、数学は世界の真理に到達するための確実な方法であると一般に認められていたため(ユークリッドの一般概念と仮定は実際に正しいものとされていた)、ここに宇宙を理解するための戦略がある。 ケプラーを非合理と呼ぶ人もいるが、この希望に満ちた認識論は、物事は理性によらない洞察に頼った不正確な方法でしか理解できないという神秘主義者の確信とは全くかけ離れていることは、注目に値するだろう。 ケプラーは確かに、洞察力を与えてくれた神への感謝を繰り返しているが、その洞察力は合理的なものとして提示されている。 算術、幾何学、天文学、音楽の4つの数理科学が含まれるのが原則であった。 しかし、何を教えるかは大学によって違っていたようだ。 チュービンゲンでは、ケプラーは当時を代表する天文学者ミヒャエル・メストリン(1550-1631)から天文学を教わっていた。 天動説では、月、水星、金星、太陽、火星、木星、土星の7つの惑星が地球の周りを回り、その円運動を組み合わせて恒星との位置関係を計算するとされています。 このシステムは、現在の(アリストテレスの)物理学の概念とほぼ一致していた。しかし、自身の中心ではなく、別の点(「等値」と呼ばれる)を中心にした円運動を「一様」(したがって明らかに永遠であると認められる)と考えることができるかなど、いくつかの難点もあった。 しかし、全体的には、天文学者(自分を「数学者」とみなしていた)は、惑星の位置を計算し続けることに満足し、その数学モデルが物理的メカニズムに対応しているかどうかを心配するのは、自然哲学者に任せていたようである。 ケプラーはこのような態度をとらなかった。 チュービンゲンでは、数学だけでなく、ギリシャ語やヘブライ語(いずれも聖典を原語で読むために必要)も学んだ。 授業はラテン語で行われた。 1年目の終わりには、ケプラーは数学以外すべてでA評価を得ていた。 おそらくメストリンは、ケプラーにもっといい成績が取れると言いたかったのだろう。実際、ケプラーは、コペルニクスの新しい天動説を紹介し、より高度な天文学を教えるために選ばれた生徒の一人であったからだ。 ケプラーはメストリンから、『回転について』の序文にある「これは単なる数学である」という説明がコペルニクスのものではないことを知ったのである。 ケプラーは、コペルニクス体系が物理的に正しいことを即座に受け入れたようである。それを受け入れた理由は、彼の最初の宇宙論モデル(下記参照)に関連して議論される。 ケプラーがこのプロテスタントの正統派に対して抱いた問題は、聖体の教義における物質と「霊」(非物質的存在)の関係であった。 このことは、ケプラーの天文学にも関連しており、太陽からの「力」がどのように惑星に影響を与えるかを説明する際に、同じような知的困難を感じていたようである。 ケプラーの著作では、歴史家にとって都合の良いように、自分の意見をはっきりと述べている。 実際のところ、このようなオープンな性格が、テュービンゲンの当局が彼の宗教的な正統性に疑問を抱くきっかけとなったのだろう。 メストリンがケプラーに聖職に就くことを断念させ、グラーツで数学を教える職に就かせたのも、そのためであろう。 その後、宗教的な不寛容さはますます強まっていった。 1612年、ケプラーは破門された。 しかし、帝室数学者という比較的高い社会的地位にもかかわらず、破門を解くことはできなかった。
ケプラーの最初の宇宙論的モデル(1596)
地動説に基づく標準的な天文学では7つの惑星がありますが、コペルニクス体系では6つしかありません。 さらに、地動説的な天文学では、惑星の球の相対的な大きさを観測で求める方法がなく、単に接触していると考えられていたのです。 これは、「恒星」(その模様によって星座が構成される)の球の一つ(あるいは二つ)先の、土星の球を越えた一番外側の球の動きによって全システムが回転するという自然哲学者の信念にうまく合致していたので、説明は不要と思われた。 コペルニクス体系では、各惑星の運動の年輪成分が地球の年輪運動の反映であることから、観測によって各惑星の軌道の大きさを計算することができ、その結果、惑星間に大きな空間があることが判明したのである。 なぜこのような空間があるのか。
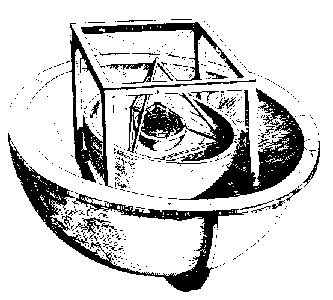
この疑問に対するケプラーの答えは、『宇宙論的神秘』(1596年、チュービンゲン刊)に書かれているが、20世紀の読者には奇異に映っただろう(右図参照)。 彼は、土星の軌道の内側に接するように球を描き、その球に立方体を内接させると、その立方体に内接する球は木星の軌道を周回する球になると提案した。 次に、木星の通り道を記した球体に正四面体を描くと、その正四面体の内接面は火星の通り道を記した球体となり、さらに内側に向かって、火星と地球の間に正十二面体、地球と金星の間に正二十面体、金星と水星の間に正八面体を配置することになる。 これは、惑星の数を完璧に説明するもので、凸の正方形は5つしかない(ユークリッドの『エレメント』第13巻で証明されている)。 また、コペルニクスの推論した軌道の大きさとも納得のいく適合が得られ、最大の誤差は10%以下であった(これは、現在でも宇宙論モデルとしては目を見張るほど良いものである)。 ケプラーは誤差の割合で表現したわけではなく、彼の宇宙論は実際、最初の数学的宇宙論モデルであるが、なぜ彼が観測的証拠が自分の理論を裏付けていると考えたかは容易に理解できるだろう。 ケプラーは自分の宇宙論をコペルニクス説の根拠とするものであると考え、自分の宇宙論を発表する前に、コペルニクス説の信憑性を証明するための議論を行った。 ケプラーは、地動説に対する利点は、その説明力の高さにあると主張している。 例えば、金星や水星は地球と太陽の間にあり、太陽から遠く離れて見えることはないが、地動説ではその説明がつかないことを、コペルニクス説では説明できる。 ケプラーは、『宇宙誌の謎』(Mysterium cosmographicum)の第1章で、このような疑問点を9つ挙げています。 観測から導かれる値との一致は正確ではなく、より良い観測によって一致が改善されることを期待したケプラーは、当時最も優れた観測天文学者の一人であるティコ・ブラーエ(1546 – 1601)に『宇宙誌の神秘』の写しを送った。 当時、神聖ローマ帝国の首都プラハで仕事をしていたティコは、実はすでにメストリンに数学の助手を求めて手紙を出していたのである。 ケプラーはこの仕事を引き受けた。
「火星との戦争」
当然ながら、ティコとケプラーの優先順位は同じではなかった。 ティコが亡くなり(1601年)、ケプラーが帝室数学者としてティコの後を継いだ後も、彼はこの問題に取り組み続けた。 従来、軌道は円の組み合わせであり、円の半径や位置を特定するために必要な観測値はほとんどなかった。 ティコは膨大な量の観測を行い、ケプラーはそれを最大限に活用することを決意した。 ケプラーは、膨大な数の観測データを駆使し、一度作り上げた軌道を他の観測データと照らし合わせ、納得のいく軌道を作り上げたのである。 ケプラーは、火星の軌道は太陽を焦点の一つとする楕円であり(この結果を全惑星に拡大したものが「ケプラーの第一法則」)、惑星と太陽を結ぶ線は、惑星が軌道を描くときに同じ時間で同じ面積を占める(「ケプラーの第二法則」)、つまり面積が時間の尺度として用いられると結論づけたのだ。 この研究が『Astronomia nova』に掲載された後、… Ⓣ, Heidelberg, 1609)に掲載された後、ケプラーは他の惑星の軌道を発見し、他の惑星にもこの2つの法則が成り立つことを証明したのである。 ケプラーのコペルニクス論は、彼の推論と推理にとって極めて重要であった。
火星の実際の計算過程は、膨大な労力を要するもので、現存するフォリオ版の計算書は1000枚近くあり、ケプラー自身もこの仕事を「私と火星の戦争」と呼んでいる。
観測誤差
ケプラーの軌道を観測と照合する方法には、何が十分な一致として認められるかという考えを持つことが重要であった。 このことから、観測誤差という概念が初めて明示的に使われるようになった。 ケプラーのこの考え方は、少なくともティコのおかげであろう。ティコは観測機器の性能を細かくチェックしていた(ブラーエの伝記を参照)。
光学と1604年の新しい星
火星に関する研究は1605年には基本的に完了していたが、本の出版が遅れていた。 一方、月を直接観測した場合とカメラ・オブスキュラを用いて観測した場合とで見かけの直径が異なるという懸念に対して、ケプラーは光学に関する研究を行い、カメラ・オブスキュラに関する最初の正しい数学的理論と、網膜上に逆さの絵ができる人間の目の働きに関する最初の正しい説明を考え出した。 これらの成果は『Ad Vitellionem paralipomena, quibus astronomiae pars optica traditur Ⓣ』(フランクフルト、1604年)に掲載された。 また、現在「ケプラーの超新星」と呼ばれている1604年の新星について書き、数々の説明を否定し、この星はもちろん特別な創造物かもしれないが、その前に他のすべてを試すべきだと思う、と発言したこともある De stella nova Ⓣ, Prague, 1606, Chapter 22, KGW 1, p.257, line 23.です。世界の調和
ケプラーの帝国数学者としての主要業務は、ティコの観測に基づく天文表の作成だったが、本当にやりたかったことは、1599年から『宇宙の神秘』の発展形として計画した「世界の調和」を書くことであった。 宇宙論に関するこの第二の著作(Harmonices mundi libri V Ⓣ, Linz, 1619)では、多面体はそのままだが、先の著作よりも精巧な数学的モデルが提示されている。 この著作の数学には、テッセレーションを初めて体系的に扱い、13個の凸の均一な多面体(アルキメデス立体)しか存在しないことの証明、2個の非凸の正多面体についての最初の説明が含まれている(すべて第2巻に収録されている)。 また、『世界の調和』には、現在「ケプラーの第三法則」として知られている、任意の二つの惑星について、その周期の二乗の比は、その軌道の平均半径の三乗の比と同じになる、という法則も含まれている。 ケプラーは、当初から軌道の大きさと周期を関連付ける法則を求めていたが、他の2つの法則のように、この法則に向かってゆっくりと段階を踏むことはなかった。 実際、印刷された『天地人』の最後の部分では、第三法則が重要な役割を担っているが、実際に発見されたのは、出版が始まってからであった。 ケプラーはぎりぎりのところで修正を加えたのである。 最終的な成功の経緯は、彼自身が語っている。
…正確な時間を知りたいのなら、この千六百八十八年の三月八日に精神的に思いついたのだが、不運にも計算に供され、したがって偽として拒絶され、ついに五月十五日に戻って新しい攻撃方法を採用し、私の心の暗闇に嵐をもたらしたのである。 ブラーエの観測に関する私の17年間の労苦と、今回の研究とが相まって、非常に強力な支えとなったので、最初は自分が夢を見ていて、自分の大前提の中に結論があると思い込んでいたのである。 しかし、「任意の2つの惑星の周期時間の間の比率は、それらの平均距離の正確な正二乗比例である」
(Harmonice mundi Book 5, Chapter 3, trans. Aiton, Duncan and Field, p.411)
Witchcraft trial
ケプラーが「世界の調和」に取り組んでいる間、彼の母親は魔女狩りで告発されていました。 彼はテュービンゲンの法学部の助けを借りた。 ケプラーは最終的に釈放されたが、それは少なくとも、当局が拷問を行う際に正しい法的手続きを踏まなかったことに起因する技術的な異議申し立ての結果であった。 残された文書は冷酷なものである。 しかし、ケプラーは仕事を続けた。 母親の弁護のためにヴュルテンベルク州に向かう途中、馬車でヴィンチェンツォ・ガリレイ(1520頃~1591、ガリレオの父親)の音楽理論に関する著作を読み、『世界の調和』にはそのことが数多く引用されています。 そのため、1616年にネイピアの対数に関する著作(1614年出版)に出会ったときは、ケプラーは大喜びであった。 しかし、メストリンはすぐに、まじめな数学者が単なる計算の補助に喜ぶのはみっともない、対数は誰もその仕組みを理解していないので、信用するのは賢明でない、と言った。 (ケプラーは、2番目の反論に対する答えとして、対数がどのように働くかを、非の打ち所のない立派な資料に基づいて証明し、発表したのである。 ユークリッドの「エレメント・ブック5」である。 ケプラーは、8桁の対数表を計算し、「ルドルフの表」(Ulm, 1628年)として出版した。 天文表はティコの観測だけでなく、ケプラーの最初の2つの法則も用いている。 新しい観測を利用した天文表はすべて、出版後数年間は正確であった。 しかし、ルドルフの天文表は、何十年にもわたって正確であることが証明された。 そして、年月が経つにつれて、表の正確さが持続することは、当然のことながら、ケプラーの法則の正しさ、ひいては天動説の正しさを証明するものと見なされたのである。 ケプラーは、帝室数学者としての退屈な公務を全うしたことで、コペルニクス理論の確立に貢献するという、彼の悲願を達成することになったのである。
Wallenstein
ルドルフの表が出版される頃には、ケプラーはもはや皇帝のためではなく(1626年にリンツを離れていた)、30年戦争(1618-1648)で成功した数少ない軍事リーダーの一人、アルブレヒト・フォン・ヴァレンシュタイン(1583-1632)のために働いていたのである。 ケプラーは当然それに従わなければならなかったが、正確な予言ができるとは思っていないことを繰り返し指摘する。 当時の多くの人々と同様、ケプラーは、天体が地球上の出来事に影響を与えるという占星術の原理は受け入れていたが(最も明確な例は、太陽が季節を、月が潮の満ち引きを引き起こすこと)、コペルニクス派の彼は、星座の物理的実在性を信じていなかったのである。 彼の占星術は、天体の位置の間の角度(「占星術的アスペクト」)のみに基づいていた。 ケプラーは、従来の占星術の複雑な体系を全く軽蔑していた。 ルドルフの表』に関する借金を取り立てに行く途中、この街に滞在していた。 ケプラーは地元の教会に埋葬されたが、30年戦争で破壊され、墓は残っていない。
歴史的メモ
ケプラーの科学活動において、非合理的と思われる要素が多く取り上げられることがある。 ケプラーの科学的活動には非合理的な要素も含まれているとされ、占星術の信奉者たちはしばしば、彼の研究が自分たちの研究に科学的に正当な先行研究を提供するものだと主張する。 アーサー・ケストラーは、影響力のある著書『夢遊病者』の中で、ケプラーの火星との戦いを、近代科学に内在する非合理性の議論に仕立てた。 この2つの説得には、多くの暗黙の信奉者がいた。 しかし、どちらもケプラーの著作の非常に部分的な読解に基づいている。 特にケストラーは、ケプラーの手順を理解するための数学的な専門知識を持っていなかったようだ。 ケプラーの研究で本当に重要な非合理的要素は、彼のキリスト教である。 ケプラーは数学を多用して成功したため、彼の仕事は「現代的」に見えるが、実際にはキリスト教の自然哲学者が相手であり、宇宙の本質を理解することは、その創造主の本質を理解することでもあった。