下の周波数表で、A=440Hz、そして
A#=466.16Hz,
B=493.88Hz,
C=523.25Hz など。
またミドルCは261.63Hzです。
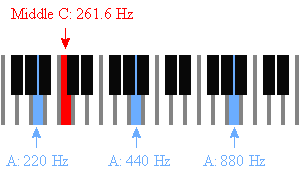
Table of Musical Frequencies
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
130.82
138.59
146.83
155.56
164.81
174.61
185
196
207.65
220
233.08
246.94
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
Frequency
261.63
277.18
293.66
311.13
329.63
349.23
369.99
392
415.3
440
466.16
493.88
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
周波数
523.25
554.37
587.33
622.25
659.26
698.46
739.99
783.99
830.61
880
932.33
987.77
Note
C
C#
D
D#
E
F
F#
G
G#
A
A#
B
C
Frequency
1046.B>
C
B>C C
B
C
A #
C#
B
C #
C#
B
C
C
C
C
C 1108.73
1174.66
1244.51
1318.51
1396.91
1479.98
1567.98
1661.22
1760
1864.66
1975.53
2093.00
これらは、
周波数 `= 440×2^(n”/”12)`
で、`n = -21, -19, …., 27`
この式はどこから来たのでしょうか?
この問題は、以前「お金の数学」で出会った複利を思い出させました。
この関係をグラフにすると次のようになります:
frequency `= 440×2^(n”/”12)`
これは以前、指数関数のグラフで扱った指数曲線です。
均等調律
何百年もの間、楽器製造者は興味深い問題に直面してきました。 バイオリン(あるいはビオラやフレットのない弦楽器)ではこれが可能で、「440×1.5=660 “Hz”」で美しい完全なEを演奏することができるのです。 しかし、(上の周波数表から)同じ音を弾くピアノは、E `= 659.26
約400年前、鍵盤(通常はハープシコードやオルガン)は、すべての楽器(特に弦)がその鍵盤で「正しく」響くように、特定の鍵盤群に合わせて調律されました。 チェンバロはそのキーでは素晴らしい音を出すが、他の関係ないキー(例えばB♭)ではかなりひどい音を出すのだ。
バッハの時代には、ミーントーン(長調の3rdをよく響かせることを目指したが、長調の5thの質にはあまりこだわらず、使えない調もあった)、作曲家がどの調でも音楽を作れるようにしたヴェルクマイスターの1691年の調律(調によって音色が異なる)などが実際に使われていたようです。
20世紀初頭、キーボードの音符が等間隔になるように調律することが決定された(上に示した表のような周波数になる)。 これをイコールテンパード・チューニングという。 バッハの時代にはこのような調律が知られていましたが、あまりにも「素っ気ない」(すべての鍵盤が同じ音質)とみなされ、正確な調律を可能にする周波数測定器もなかったため却下されました。
残念ながら、平均律の調律は、キーボードも関係すると楽器間の調律のわずかな違いを許容しなければならないことを意味しています。 弦楽器は通常、このような理由から、他の弦楽器だけで演奏するのが最も幸せです。
top
検索 IntMath
Online Trigonometry Solver
This trigonometry solver can solve of math problems.
Go to: オンライン三角法ソルバー