先に述べたように、電荷の連続した流れが発生するためには、単に経路(=回路)があるだけでは不十分で、電荷キャリアを回路の周りに押しやる何らかの手段も必要です。 管の中のビー玉やパイプの中の水のように、流れを起こすには何らかの影響力が必要なのである。 電子の場合、この力は静電気で働く力と同じで、電荷のアンバランスによって生じる力である。 蝋と羊毛をこすり合わせた場合、蝋の電子は余り(負電荷)、羊毛の電子は不足(正電荷)しているため、両者の電荷はアンバランスな状態にあることがわかる。 このアンバランスは、2つの物体間の引力として現れます。

充電された蝋と羊毛の間に導電線を置くと、蝋の余剰電子の一部が電線を通って羊毛に戻り、そこの電子の不足を埋めるので、電子はその中を流れるようになります。

ワックスの原子とウールの原子の間の電子のアンバランスは、2つの材料の間に力を生み出します。 ワックスからウールへ電子が流れる道がないため、この力は2つの物体を引き寄せるだけです。 しかし、絶縁体の隙間を導体が埋めることで、その部分の電荷が中和され、ロウとウールの間の力が弱まるまで、その力は一瞬ではあるが、電子を一様に電線の中を流れるようにさせる。 このように、2つの素材をこすり合わせることで生まれる電荷は、ある種のエネルギーを蓄える役割を担っている。 このエネルギーは、低いレベルの池から汲み上げた水の高い貯水池に蓄えられたエネルギーと似ていない:
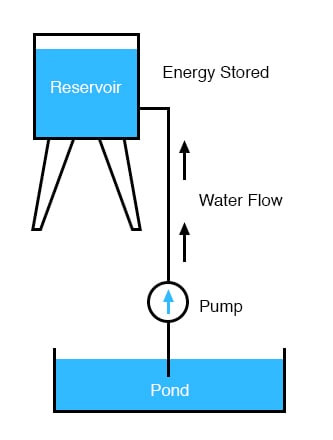
貯水池の水に対する重力の影響は、水を再び低いレベルへ移動させようとする力を生み出す。
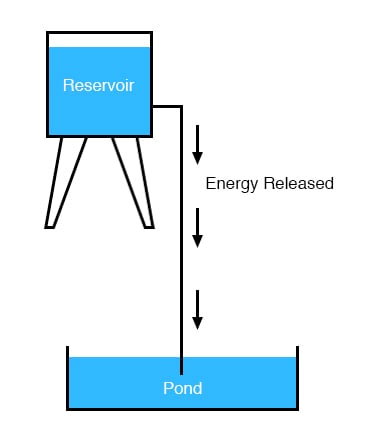
その水を低いレベルの池から高いレベルの貯水池に送るにはエネルギーが必要で、配管を通って元のレベルに戻る水の動きは、前のポンプで蓄えたエネルギーの放出になる。 水がさらに高いレベルまで汲み上げられると、そうするためにさらに多くのエネルギーが必要となり、したがって、より多くのエネルギーが蓄積され、水がパイプを通って再び下に流れるようになると、より多くのエネルギーが放出されます:

電子はあまり変わりません。 蝋と羊毛をこすり合わせると、電子を通常の「レベル」から「ポンプ」して、電子が元の位置 (とそれぞれの原子内のバランス) を再確立しようとする力が蝋と羊毛の間に存在する状態を作り出します。 電子を元の位置に引き戻す力は、貯水池の水を元の高さに引き下げようとする重力のようなものです。 水を汲み上げるとエネルギーが蓄積されるように、電子を汲んで電荷のアンバランスを作ると、そのアンバランスにある量のエネルギーが蓄積されるのである。 そして、貯水池の高さから水が逆流するように、電子が元の「レベル」に戻るようにすれば、蓄積されたエネルギーが放出されることになる。
Understanding the Concept of Voltage
When the charge carriers are poised in that static condition (just like water sitting still, high in a reservoir), the energy stored there is called potential energy, because it has the possibility (potential) of release that has not fully realized yet.というわけで電荷キャリアが静止状態にあるときは、そこに蓄えられるエネルギーは潜在エネルギーと呼ばれています(ちょうど水がじっと、貯蔵池の中の高いところにあるような状態)。 乾燥した日に布製のカーペットにゴム底の靴をこすりつけると、自分とカーペットの間に電荷のアンバランスが生じます。 足で靴擦れをすることで、電荷のバランスが崩れ、エネルギーが蓄積されるのです。 この電荷(静電気)は静止しているので、エネルギーが蓄積されていることに全く気づきません。 しかし、金属製のドアノブ(電荷を中和する電子移動度が高い)に手を当てると、蓄積されたエネルギーが電荷の流れとなって手に放出され、電気ショックとして認識されるのです。 この電位エネルギーは、電荷の不均衡という形で蓄積され、電荷キャリアを導体中を流れるように促すことができ、電圧という用語で表すことができます。
The Definition of Voltage
静電気の文脈で定義すると、電圧とは、電荷のバランスを保とうとする力に対して、ある場所から別の場所に単位電荷を移動するのに要する仕事の指標となります。 電圧は位置エネルギーの表現であり、電荷がある「レベル」から別の「レベル」に移動する際のエネルギー放出の可能性や潜在性を表すため、常に2点間で参照されます。 貯水池に例えて考えてみましょう。

落下の高さに差があるため、貯水池から配管を通って場所 2 に放出されるエネルギーの方が場所 1 に放出されるエネルギーよりもはるかに大きいという可能性があります。 この原理は、石を落とすことで直感的に理解できます。1フィートの高さから落とした石と、1マイルの高さから落とした同じ石とでは、どちらがより激しい衝撃をもたらすでしょうか。 明らかに、高さから落とした方が、より大きなエネルギーを放出する(より激しい衝撃を与える)。 貯水池に蓄えられたエネルギーは、水の体積だけでは評価できませんし、落石の衝撃は岩の重さだけでは予測できません。 質量が落下するときに放出されるエネルギー量は、落下開始点と落下終了点の距離に比例する。 同様に、電荷キャリアをある点から別の点へ移動させるのに利用できる位置エネルギーは、その2点間の相対的なものである。 したがって、電圧は常に2点間の量として表現されます。 興味深いことに、質量がある高さから別の高さに「落ちる」というアナロジーは、2 点間の電圧を電圧降下と呼ぶことがあるほど、適切なモデルです。 化学反応、放射エネルギー、導体への磁気の影響などが、電圧を発生させる方法として挙げられます。 この3つの電圧源には、バッテリー、太陽電池、発電機(自動車のボンネットにある「オルタネーター」ユニットなど)がそれぞれ該当する。 重要なのは、電圧源を利用して電気回路に電荷を流す方法を理解することです。

電圧源の仕組み
電池を含む電圧源は、電気的に接触する2つのポイントを持っています。 この場合、上の図では1点と2点です。 長さの異なる水平線は、これが電池であることを示し、さらにこの電池の電圧が電荷キャリアを回路に押し出そうとする方向を示しています。 電池記号の横線が離れている(電荷の通り道になっていない)ように見えるのは、実際のところ、横線は液体または半固体材料に浸された金属板で、電荷を伝導するだけでなく、金属板と相互作用して電圧を発生させて電荷を押し流すからである。 電池のマークの左側にある小さな「+」と「-」の記号に注目してください。 電池のマイナス(-)の端は常にダッシュが短いほうで、電池のプラス(+)の端は常にダッシュが長いほうです。 電池のプラス端は、電荷キャリアを押し出そうとする端です(慣習上、電子はマイナスに帯電していても、電荷キャリアはプラスに帯電していると考えることを覚えておいてください)。 同様に、マイナス端は、電荷キャリアを引き寄せようとする端です。 電池の「+」と「-」の端が何も接続されていない状態では、その 2 点間に電圧が発生しますが、電荷キャリアが移動できる連続した経路がないため、電池を通過する電荷の流れはありません。

同じ原理が、貯水池とポンプのアナロジーにもあてはまります。 貯水池が完全に満たされると、ポンプでいくら圧力をかけても、流れは発生しません。 連続的に水を流すためには、池から貯水池へ、そしてまた池へというように、水が流れる道(回路)が必要なのです。 電池の端から端まで電線をつなげば、そのような経路を確保することができます。

電流の概念を理解する
電池が電圧を出し続け、電気経路の連続性が壊れていない限り、電荷キャリアは回路を流れ続けることになります。 パイプの中を流れる水の比喩にならって、回路を流れるこの連続的で均一な電荷の流れを電流と呼びます。 電圧源が同じ方向に「押し」続けている限り、電荷キャリアは回路内を同じ方向に動き続ける。 この単一方向の電流を直流(DC)と呼びます。 本シリーズの第2巻では、電流の方向が前後に切り替わる電気回路について説明します。 交流です。 しかし、今回は直流回路についてだけ説明します。 電流は、ビー玉が筒の中を、水がパイプの中を流れるように、個々の電荷担体が前方の電荷担体を押しながら移動し、導体の中を一様に流れるものだから、一つの回路中の流れる量はどの地点でも同じになる。 もし、一つの回路の電線の断面をモニターして、流れていく電荷キャリアを数えたとしたら、導体の長さや導体の直径に関係なく、単位時間あたりの量は他の部分と全く同じであることに気づくはずだ。 回路の導通をどこかで断つと、電流はループ全体で停止し、電池によって生成された全電圧が、接続されていた電線の端の間で、断線の向こう側に現れます:

電圧降下の極性とは何か?
断線の両端に描かれた「+」と「-」の記号と、電池の端子の隣にある「+」と「-」の記号に注目してください。 これらの印は、電圧が電流を押し出そうとする方向、一般に極性と呼ばれるその電位方向を示しています。 電圧は常に2点間の相対的なものであることを忘れないでください。 このため、電圧降下の極性も2点間の相対的なものであり、回路内のある点が「+」と表示されるか「-」と表示されるかは、その点が参照する他の点によって決まる。 次の回路を見てみよう。ループの各コーナーには、参考までに番号が付けられている。

2点と3点の間で回路の導通が切れているので、2点と3点の間に落ちる電圧の極性は、2点が「+」で3点が「-」となる。 電池の極性(1「+」、4「-」)は、ループを流れる電流を1→2→3→4と時計回りに押し戻し、再び1に戻そうとしています。

3 と 4 の間に切れ目があると、この 2 点間の電圧降下の極性は、4 が「-」、3 が「+」です。 特に、3 点の「符号」が、2 点と 3 点の間で切れていた最初の例 (3 点が「-」と表示されていた) と逆になっていることに注意してください。 この回路では、ポイント 3 が常に「+」または「-」のどちらかになると言うことは不可能です。極性は、電圧自体のように、1 つのポイントに固有ではなく、常に 2 つのポイント間の相対的なものだからです!
REVIEW:
- 静電気で示されるのと同じ力により、電荷キャリアが導体を流れるように動機付けることができます。 平たく言えば、電荷を動かすために利用できる「押し」の尺度です。
- 電圧は、位置エネルギーの表現として、2 つの場所、または点の間で常に相対的なものとなっています。
- 電圧源が回路に接続されている場合、電圧はその回路を通して電流と呼ばれる電荷キャリアの均一な流れを引き起こす。
- 単一(1ループ)回路では、任意の点での電流量は他の任意の点での電流量と同じである。
- 電圧源を含む回路が断線した場合、その電圧源の全電圧が断線のポイントに現れます。
- 電圧降下の+/-の方向を極性と呼びます。
関連ワークシート:
- Voltage, Current, and Resistance Worksheet